반응형
Edge Detection
목차
0. Preview
1. 에지 검출의 기초
2. 영교차 이론
3. 캐니 에지
4. 컬러 에지
5. 선분 검출
<0~2.영교차이론>은 이전 게시글을 참고해주세요
https://codingsmu.tistory.com/105
[패턴인식] 영상 처리(2) : 이진영상, 영상 처리의 세가지 기본 연산
Digital Image Processing 목차 0. Preview 1. 디지털 영상이란? 2. 히스토그램 3. 이진 영상 4. 영상 처리의 세가지 기본 연산 5. 다해상도 6. 모폴로지 7. 컬러 은 이전 게시글을 참고해주세요 https://codingsm..
codingsmu.tistory.com
3. 캐니 에지
- 앞 절은 '그럴듯해 보이는' 에지 연산자 사용
- 캐니 에지(Canny Edge)
- 1986년에 발표 : A Computational approach to edge detection, J Canny, 1986
- 에지 검출을 최적화 문제로 해결
- 세가지 기준
- 최소 오류율 : 거짓 긍정과 거짓 부정이 최소. 즉, 없는 에지가 생성되거나 있는 에지를 못찾는 경우를 최소화해야함
- 위치 정확도: 검출된 에지는 실제 에지의 위치와 가급적 가까워야한다
- 에지 두께 : 실제 에지에 해당하는 곳에는 한 두께의 에지만 생성해야함
- 캐니 에지 검출 알고리즘
- input: 영상 $f(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1$
- output : 에지 영상 $e(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1$ // 에지는 1, 비에지는 0인 이진 영상
- 입력 영상 f에 $\sigma $ 크기의 가우시안 스무딩을 적용
- 결과 영상에 소벨 연산자를 적용하여 에지 강도와 에지 방향 맵을 구함
- 비최대 억제를 적용하여 얇은 두께 에지 맵을 만듦
- 이력 임계값을 적용하여 거짓 긍정을 제거
- 비최대 억제
- 이웃 두 화소보다 에지 강도가 크지 않으면 억제됨

비최대 억제를 위한 두 이웃화소(방향 4는 0, 5는 1, 6은 2, 7은 3과 같음)
- 이력 임계값
- Hystresis thresholding
- 두 개의 임계값 $T_{high}$와 $T_{low}$ 사용하여 거짓 긍정 줄임
- 에지 추적은 $T_{high}$를 넘는 화소에서 시작, 추적 도중에는 $T_{low}$ 적용
- Hystresis thresholding
- 캐니 에지 검출
- input: 영상 $f(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1$, 가우시안의 표준편차 $\sigma$ , 이력 임계값 $T_{high}$와 $T_{low}$
- output : 에지 영상 $e(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1$ // 에지는 1, 비에지는 0인 이진 영상
-
# image f, Gaussian filter G(sigma = s) g = f*G # sobel mask apply into g, get the magnitude of edge S and direction of edge D # ref_D is two-neigbor pixel for non-maximum suppression ref_D = [[(x,y+1),(x,y-1)], [(x+1,y+1),(x-1,y-1)], [(x-1,y),(x+1,y)], [(x-1,y+1),(x+1,y+1)]] # Non-maximum Suppression for y in range(1,M-1): for x in range(1, N-2): # (y,x)'s neighbor pixels y1,x1 = ref_D[D][0] y2,x2 = ref_D[D][1] if S(y,x) <= S(y1,x1) or S(y,x) <= S(y2,x2): S(y,x) = 0 # Non-maximum Suppression # edge tracking by hysteresis threshold e = [[0]*N for _ in range(M)] visited = [[0]*N for _ in range(M)] for y in range(1,M-1): for x in range(1,N-2): follow_edge(y,x) # edge tracking recurssion funciton def follow_edge(y,x): visitied[y][x] = 1 # visited e[y][x] = 1; # (y,x) pixel is edge for nys, nxs in ref_D:# 8-neigbor for ny, nx in nys, nxs: if S(ny, nx) > T_low and not visited[y][x]: follow_edge(ny,nx)
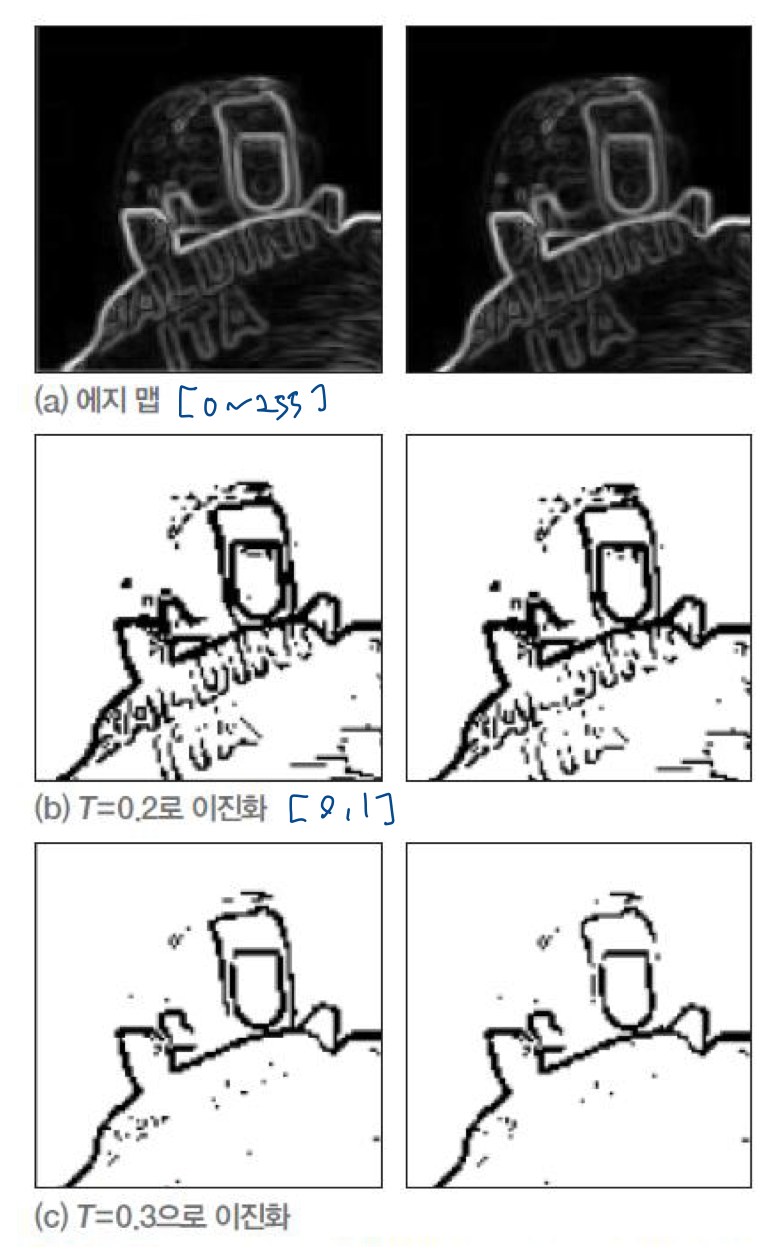
- 캐니 에지 검출 예시

캐니 에지
4. 컬러 에지
- RGB 채널에 독립적으로 적용 후 OR 결합
- 에지 불일치 발생

- 디젠조 방법

- 적용 예시
디젠조 에지 맵(왼쪽)과 RGB채널을 평균한 에지 맵(오른쪽)
5. 선분 검출
- 에지 맵 -> 에지 토막 -> 선분
5.1 에지 연결과 선분 근사
- 에지 연결과 표현

에지 토막의 에지 여로가 체인코드 표현 - 세선화(Thining)
- 2~3두께 에지를 1두께로 변환
- 최소 8-연결성 보장
- SPTA 세선화(PASS)
- 에지 추적

에지연결과정 - 지문인식, 정맥인식등에 사용됨
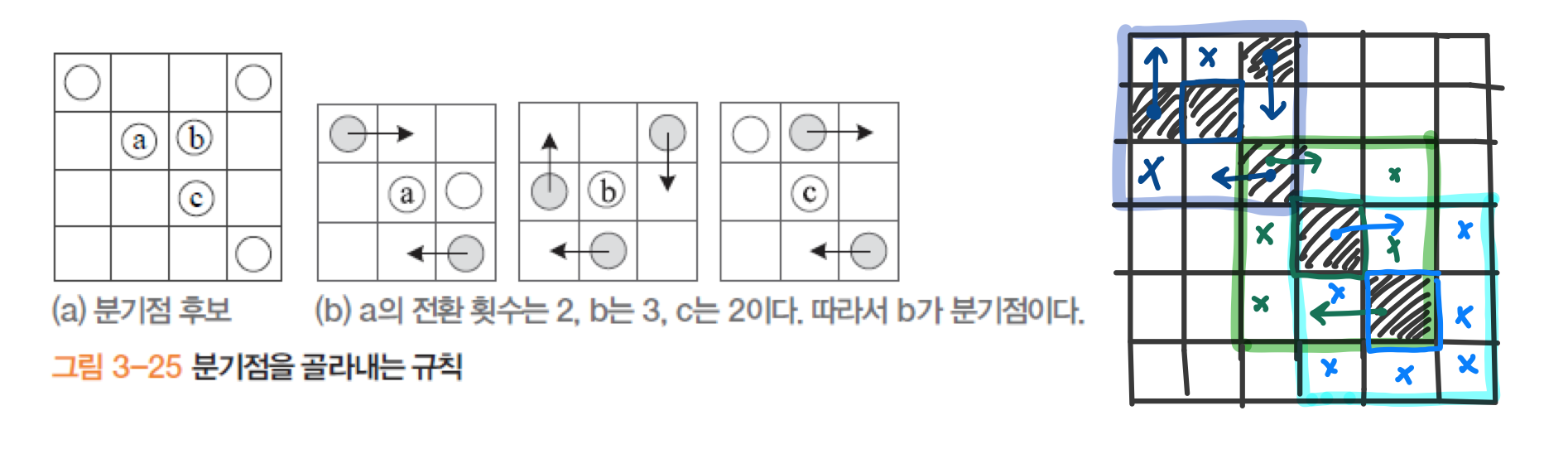
- 분기점을 골라내는 규칙 : 경계에서 경계가 아닌지점으로의 변환 수
- 분기점(3번 : 그림에서 파란 점), 일반점(2번 : 그림에서 초록 점), 끝점(1번 : 그림에서 하늘색 점),
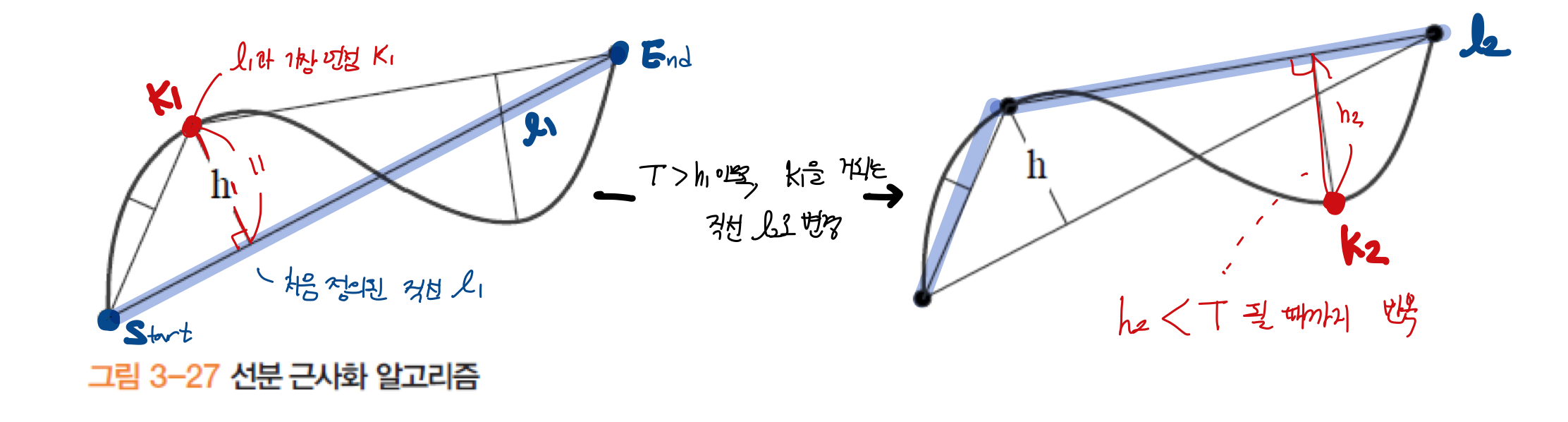
- 선분 근사
- 두 끝점을 잇는 직선으로부터 가장 먼 점까지의 거리 h가 임계값 이내가 될 때까지 선분 분할을 재귀적으로 반복
- T = 10일 때 선분 근사화 과정은 아래와 같다
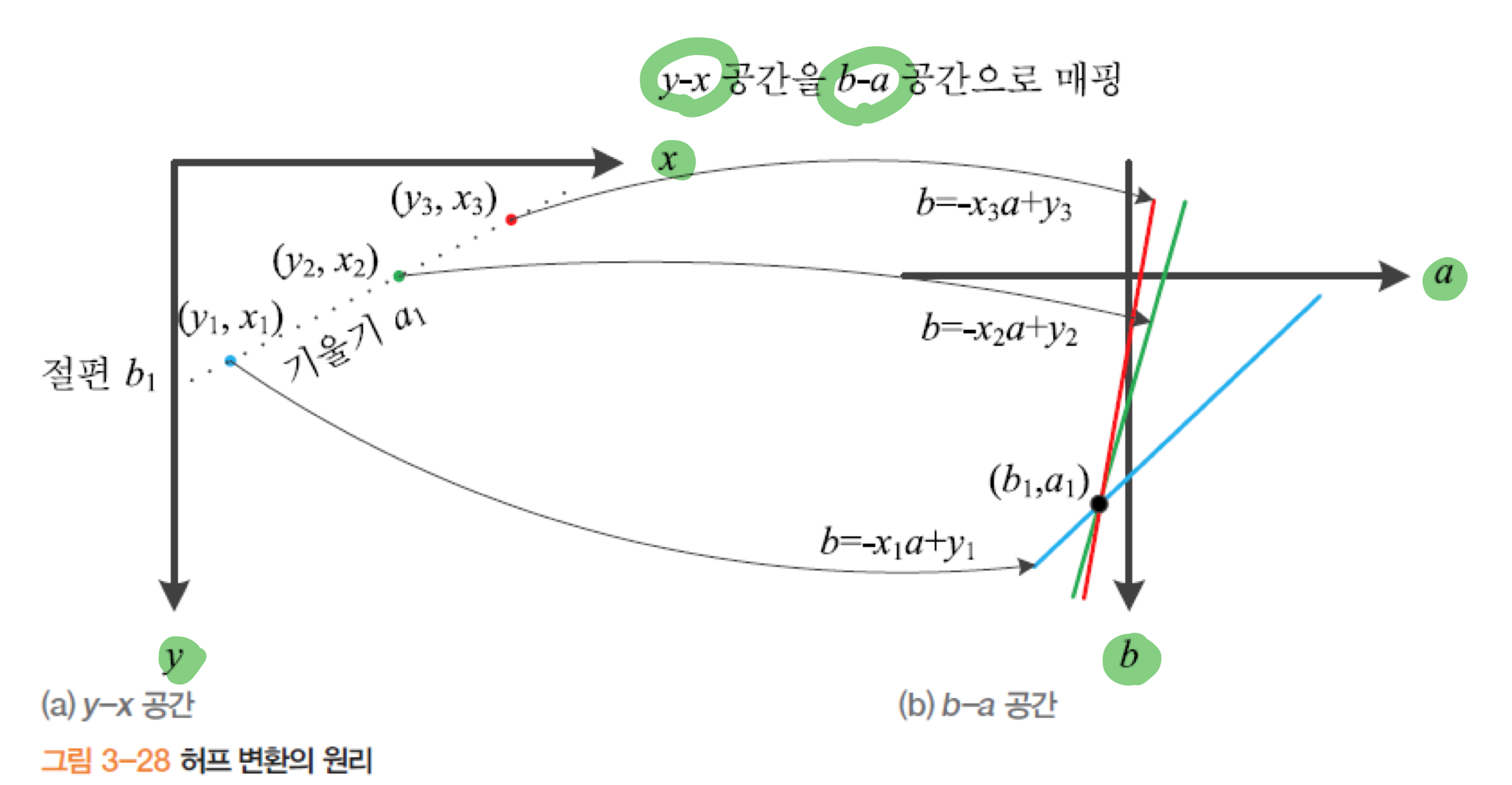
5.2 허프 변환(Hough Transformation)
- 에지 연결 과정 없이 선분 검출(전역 연산을 이용한 지각 군집화)
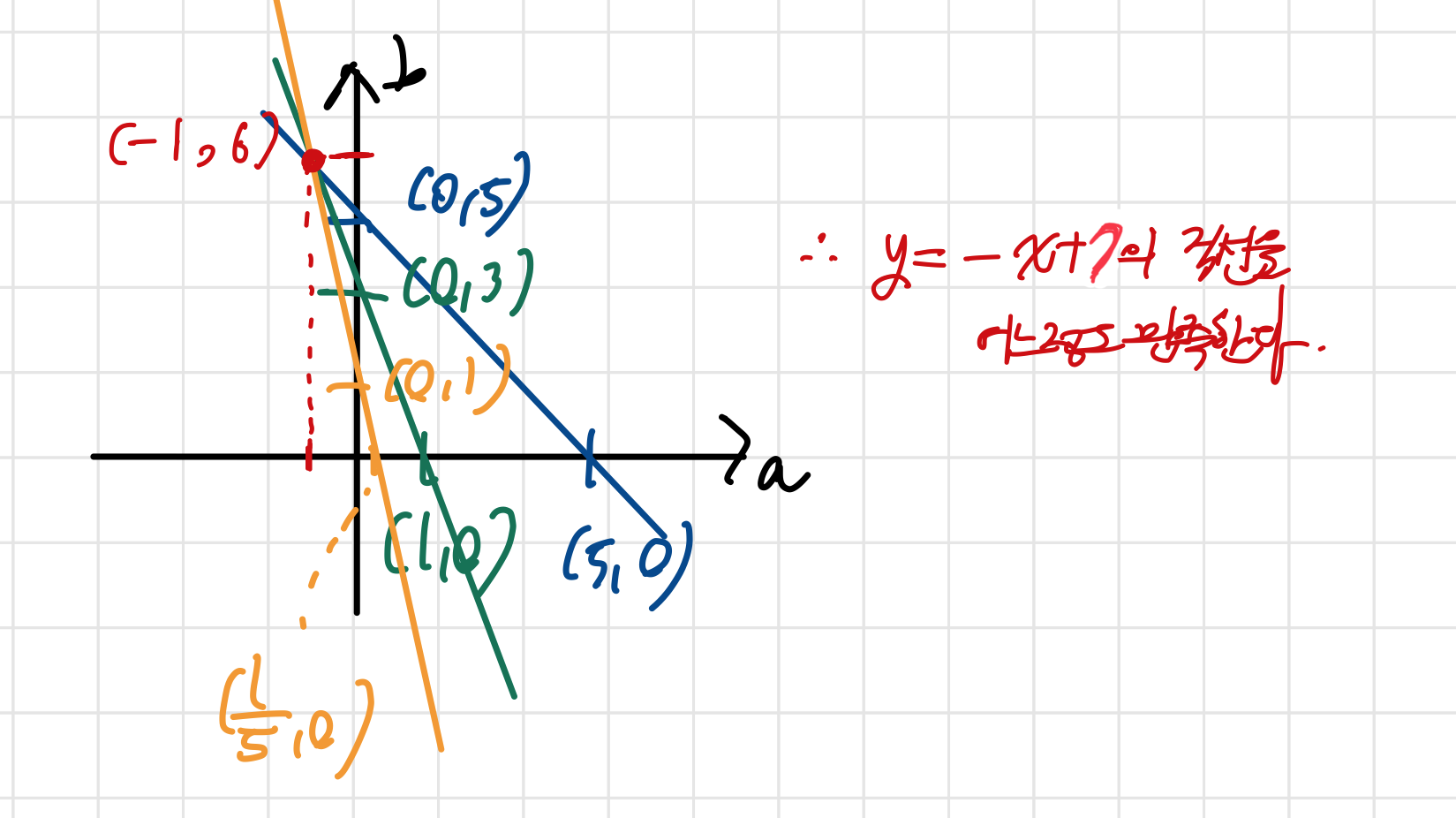
- 영상 공간 y-x를 기울기 절편 공간 b-a로 매핑
- 선분 검출 과정

- 위 과정 결과 세 직선의 교차점인 (-1,6)을 지나는 직선 y=-x+7이 어느정도 만족함을 알 수 있음
- 수직선의 기울기가 $\infty$ 인 문제
- 극좌표계를 사용하여 해결
- $ycos\theta + xsin\theta = \rho$

- 밀집된 곳 찾기
- 양자화된 누적 배열 이용하여 해결
- 알고리즘 : 직선 검출을 위한 허프 변환
- input: 에지 영상 $e(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1$, 임계값 T // 에지는 1, 비에지는 0인 이진 영상
- output: $(p_k, \theta_k), 1<= k <= n$ (n개의 직선)
- 2차원 누적 배열 A를 0으로 초기화
- for(에지영상 e에 있는 에지화소 $(y_i, x_i)$ 각각에 대해)
- $y_icos\theta + x_isin\theta = \rho$가 지나는 A의 모든 칸을 1만큼 증가시킴
- A에서 T를 넘는 지역 최대점 $(p_k, \theta_k)$를 모두 찾아 직선으로 취함
- 원 검출
- 3차원 누적 배열 사용
- $(y-b)^2 + (x-a)^2 = r^2$
- 3차원 누적 배열 사용
- 허프변환 예제
- 위의 그림 [3-29]를 이산공간에 다시 그린 것이다. 왼쪽 그림에서 세 점은 $(y_1, x_1)=(4,1),(y_2, x_2)=(2,4),(y_3, x_3)=(1,6)$이다
- $(y_1, x_1)=(3,5,1)$이면 세 점이 정확히 일직선상에 있지만 디지털 영상의 특성 상 약간의 위치 오차가 발생했다고 간주하자

- 누적배열 A를 0으로 초기화
- 세 점의 자취를 누적시키면 오른쪽 그림과 같은 배열이 된다
- 이 배열에서 지역 최대점은 3을 갖는 (6,6)으로 $(\rho, \theta) = (4,40도)$에 해당한다
- $ycos40+ xsin40 = 5$라는 직선을 검출한 셈이다
- 왼쪽 그림에 있는 점선이 검출한 직선이다
- 허프변환 oopenCV
- cv2.HoughLines()
- 기본적인 허프 변환 알고리즘 내용을 담고있는 함수
- 리턴값 : 2차원 $(r,\theta)$ 배열
- r 단위 : 픽셀(pixel)
- $\theta$ 단위 : 라디안(radian)
- cv2.HoughLinesP()
- 모든 픽셀에 대해서 계산하려면 비효율적이므로 무작위로 몇 개의 픽셀만을 사용하여 확률적으로 허프 변환을 수행하는 함수
- 리턴값 : 찾은 직선들의 좌표점 list(예: [[x1, y1, x2, y2]]
- cv2.HoughLines()
5.3 RANSAC
- RANSAC(RANdom SAmple Consensus)
- 1981년 Fischler&Bolles이 제안[Fischler81]
- 인라이어를 찾아 어떤 모델을 적합시키는 기법
- 난수 생성하여 인라이어 군집을 찾기 때문에 임의성을 지님
- 선분 검출에 적용
- 모델은 직선의 방정식 y=ax+b
-
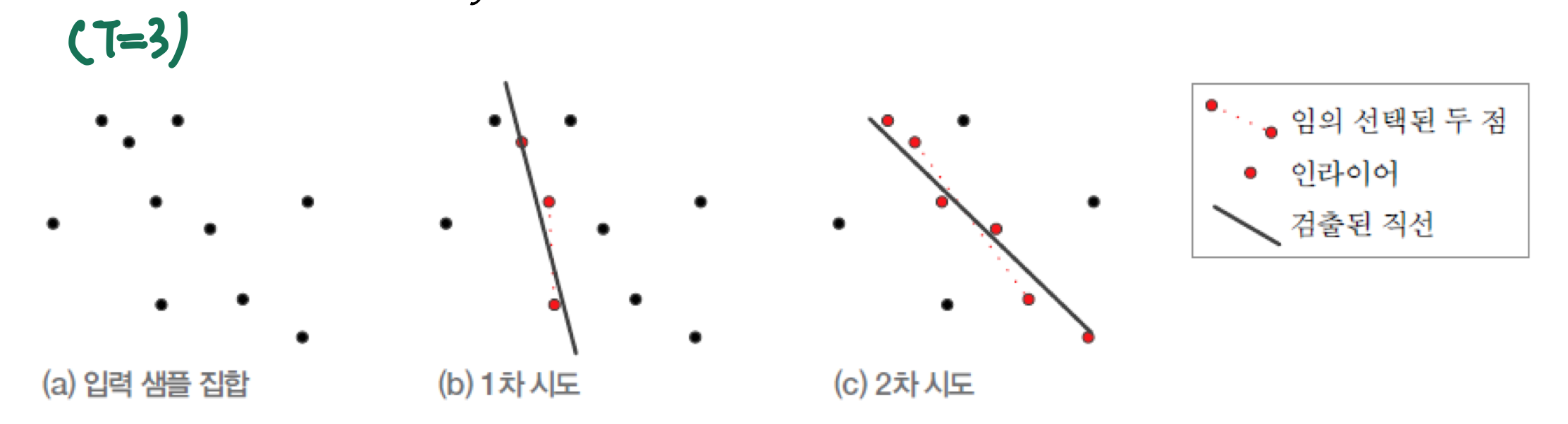
RANSAC의 원리
반응형
'인공지능(AI) > 컴퓨터비전(CV)' 카테고리의 다른 글
| [패턴인식] 지역 특징 검출(2): 스케일에 불변한 특징점 검출 (0) | 2021.12.15 |
|---|---|
| [패턴인식] 지역 특징 검출(1): 이동/회전 불변 특징점 검출, 위치 찾기 알고리즘 (0) | 2021.10.24 |
| [패턴인식] 에지 검출(1) : 에지 검출의 기초, 영교차 이론 (0) | 2021.10.24 |
| [패턴인식] 영상 처리(3) : 다해상도, 모폴로지, 컬러 (0) | 2021.10.24 |
| [패턴인식] 영상 처리(2) : 이진영상, 영상 처리의 세가지 기본 연산 (2) | 2021.10.21 |
![[패턴인식] 에지 검출(2) : 캐니 에지, 컬러 에지, 선분 검출](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FdStKC1%2FbtriHCtTFnB%2FAAAAAAAAAAAAAAAAAAAAAA3x5yJG1pXcyfEvbY4ygRGtKINgd14VazNoitfGjgVB%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DbH27mCJlPvUuHzKTwJAJKs%252Fxd84%253D)