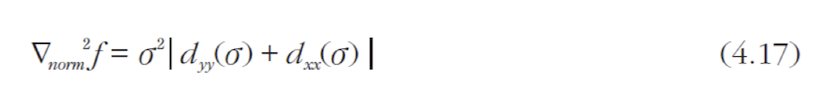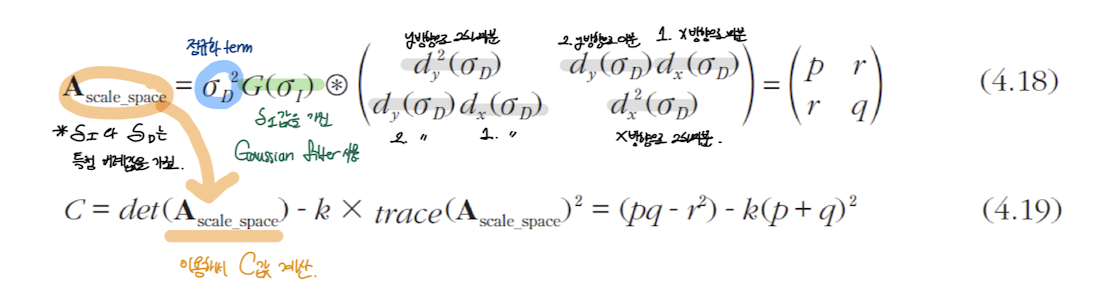[패턴인식] 지역 특징 검출(2): 스케일에 불변한 특징점 검출

Local Feature

4. 스케일에 불변한 특징점 검출

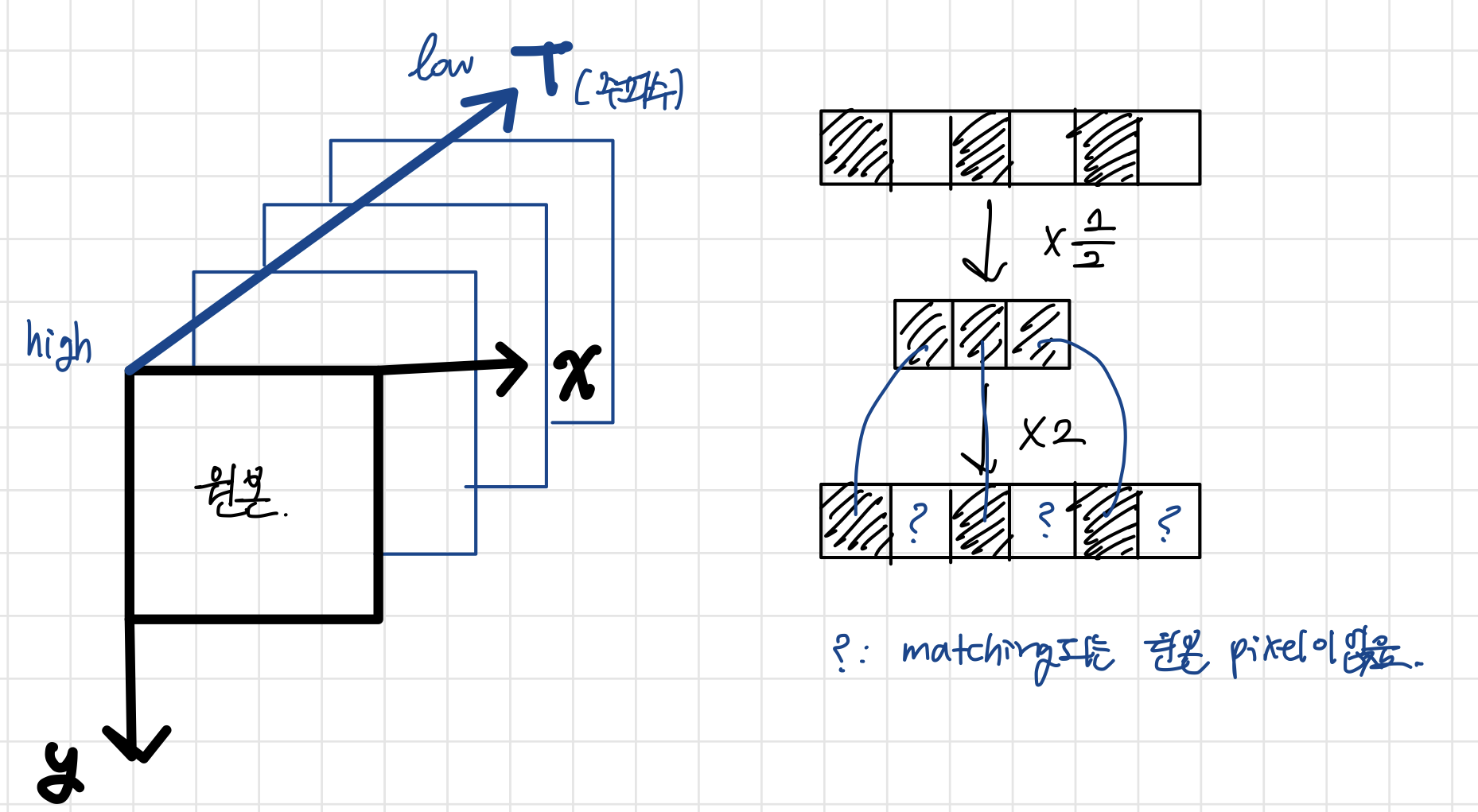
거리에 따른 스케일 변화

예로, 멀면 작고 윤곽만 어렴풋이 보이다가, 가까워지면 커지면서 세세한 부분이 보임
사람은 이에 강인하게 대처하는데 컴퓨터 비전도 과연 그러한가?
앞서 배운 해리스 코너 검출기(Harris corner detector)는 회전 불변하나 크기 불변은 아님

4.1 스케일 공간

다중 스케일 접근 방법

스케일 축이 추가된 3차원 공간에서 극점(지역 최대 또는 최소점) 검출

다중 스케일 접근 방법 알고리즘

#input = 영상 f(j,i), 0<=j<=M-1, 0<=i<=N-1, 임계값 T
#output = 특징점 리스트 F

f에서 다중 스케일 영상 M를 구성한다.
M에서 3차원 극점을 찾아 특징점 집합 F로 취한다 #극점(y,x,s)는 스케일 불변이어야 함

f에서 다중 스케일 영상 $M={f^{s^0},f^{s^1},f^{s^2}, \cdots}$를 구성 //$f^{s^i}$는 스케일이 $S_i$인 영상

영상을 줄일 경우, 단순히 물리적으로 크기가 작아질 뿐아니라, 주파수 관점에서 밝기값의 빈번함을 제대로 표현할 수 없음

다중 스케일 영상을 구현하는 두 가지 방식

가우시안 스무딩(Gaussian Smoothing): 스케일에 해당하는 $\sigma$가 연속 공간에 정의
피라미드: $\frac{1}{2}$씩 줄어드므로 이산적인 단점
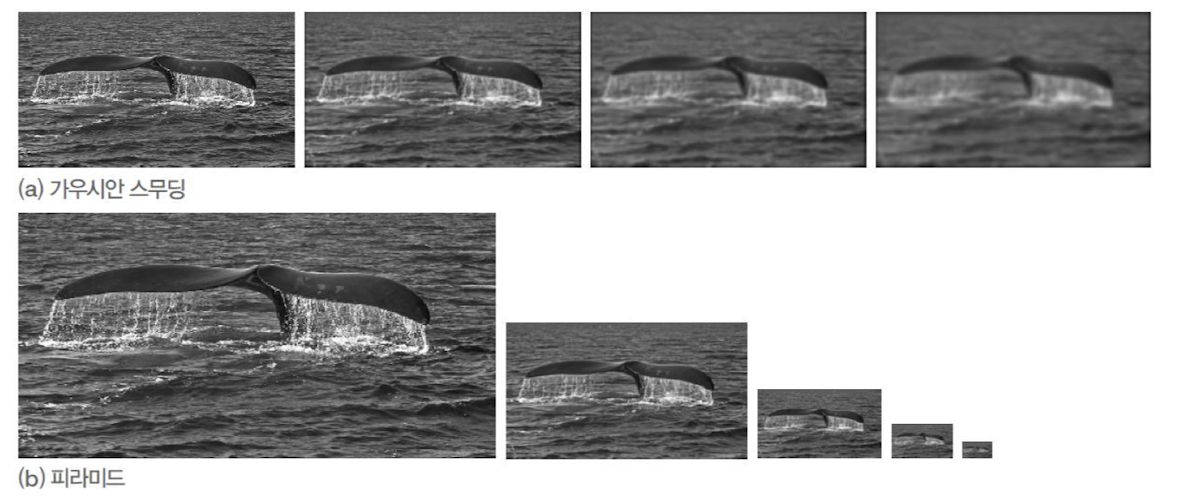
다중 스케일을 구현하는 두 가지 방식

가우시안 스무딩에 의한 스케일 공간

스케일 축을 추가한 3차원 공간
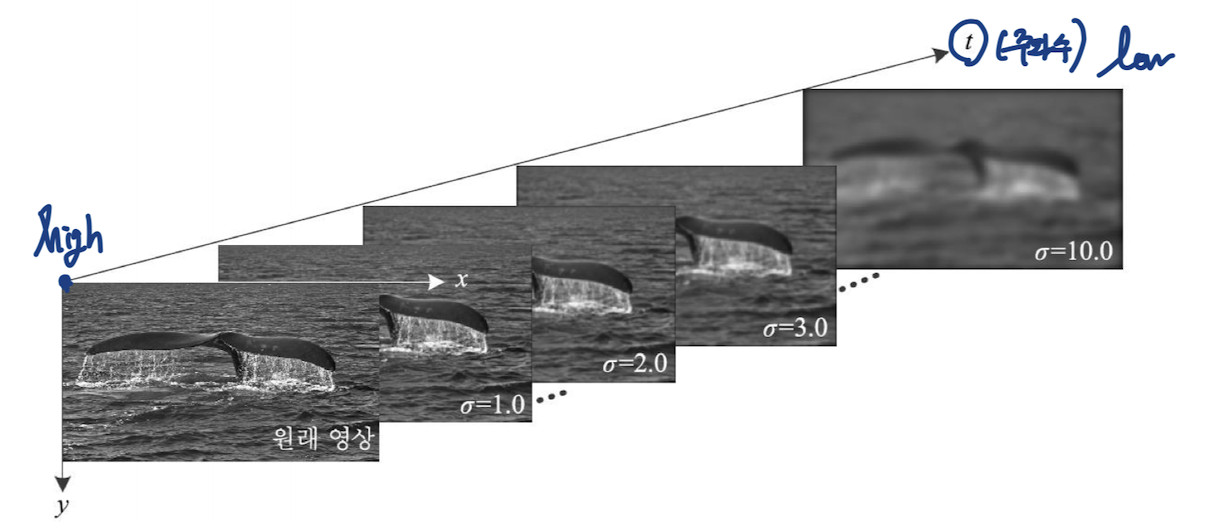
(y,x,t)로 표현되는 스케일 공간

t축에서 지역 극점 탐색

t축을 따라 정규 라플라시안(normalized laplacian)을 측정해보면 극점이 발생한다
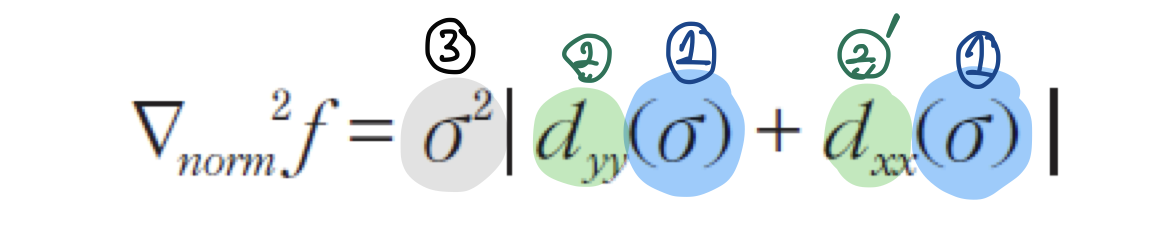
- 영상 뭉개짐(blur) 처리
  - (1) 영상에 가우시안 처리
- 가로/세로 방향으로 밝기값 변화를 살펴봐서 edge map 확인
  - (2) y축으로 2차 미분
  - (2)' x축으로 2차 미분
- 정규화
  - (3) $\sigma$를 제곱해 미분결과를 보정해줌
실험에 따르면 t축에서 정규 라플라시안이 가장 안정적으로 극점 생성
극점의 $\sigma$값은 물체의 스케일에 해당
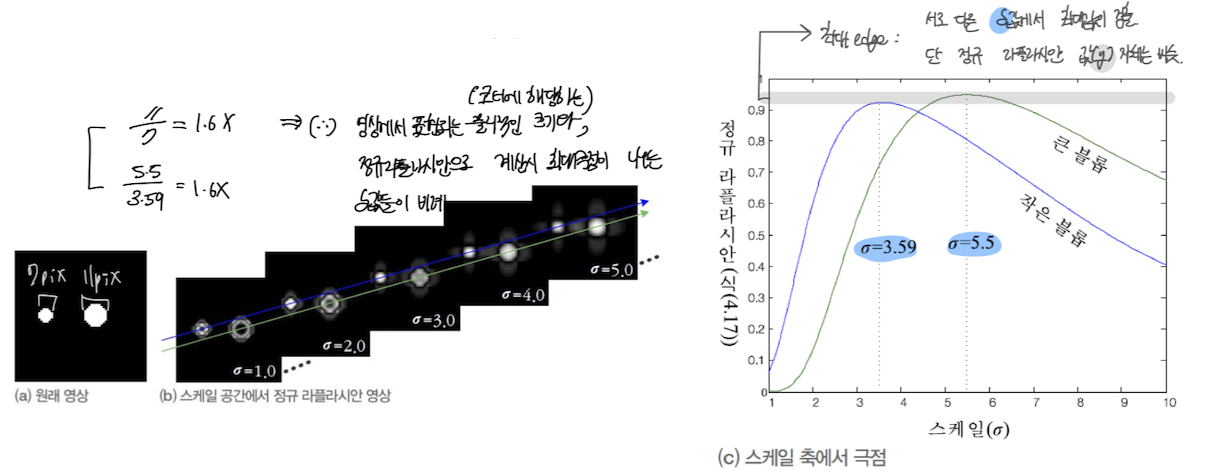
스케일 공간 (y,x,t)에서 극점 검출

4.2 해리스 라플라스 특징 검출

(y,x,t)의 3차원 공간에서 극점을 어떻게 찾는가

위의 그림은 (y,x)를 알고 있는 상황

해리스 라플라스의 전략

영상공간 (y,x)과 스케일 축 t 각각에서 잘 작동하는 식을 사용
영상 공간에서는 해리스의 식 (4.9) 사용
스케일 축에서는 정규 라플라시안(4.17) 사용
해리스의 식을 다중 스케일로 확장

해리스 라플라스 특징 검출 알고리즘

#input = 영상 f(j,i), 0<=j<=M-1, 0<=i<=N-1, 임계값 T # default c = 1.4, s = 0.7
#output = 특징점 리스트 F # F =(y_k, x_k, t_k)

F_tmp = set()


# STEP1 : add local extreme point at scale space
for n in range(N):
	sigma_n =c * sigma_0
    sigma_1 = sigma_n
    sigma_D = s * sigma_n # sigma_D == s * sigma_i relation
    
    # calculate feature map using (4.19)
    ...
    # calculate local extreme point in map, and add (y,x,sigma_1) to F_tmp
    # (y,x,sigma_1) = c
    ...
    
    
# STEP2: selection scale
# this step is detail adjustment for local extreme point that calculated previous step
F = set()
for y,x,sig in list(F_tmp):
	while True:

    	# find sigma_new(local extreme point of normalized laplacian)
        # at scale axis [0.7sig, 1.4sig]
        ...
        if not sigma_new:
        	# throw out e
            ...
            break
        else:
        	#find new extreme point (y_new, x_new) near (y,x)
            # about sigma_new
            ...
        if (y,x,sig) = (y_new, x_new, sigma_new):
        	F.add(y,x,sig) # add feature point
            break
        else:
        	(y,x,sig) = (y_new, x_new, sigma_new)

4.3 SIFT 검출

SIFT(Scale-invariant featrure Tranform)의 등장

크기, 회전, 조명에 불변한 특징 검출
1999년 David Lowe 교수의 논문
2004년 IJCV에 확장된 논문 발표
- Distinctive Image Features from Scale-Invariant Keypoints, David G. Lowe, January 5, 2004
- 성능이 뛰어나 현재 가장 널리 사용되며, 다양한 변형이 개발되어 있음

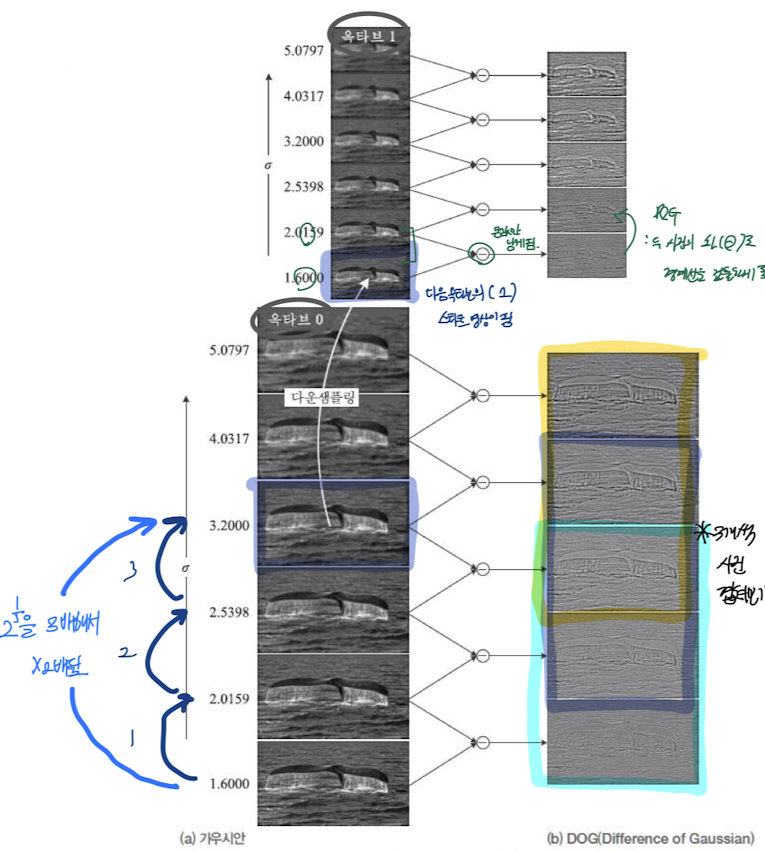
SIFT의 구조

피라미드+가우시안 구조
- 각 층은 여섯 영상의 묶음(옥타브)으로 구성
- 옥타브의 영상은 $\sigma_i$로 스무딩
- $\sigma_{i+1} = k \sigma_i (\sigma_0 = 1.6, k = 2^{1/3})$
SHIF가 사용하는 스케일 공간(DOG 피라미드 구조)

SIFT 검출 과정(자세히)

(1) 스케일 공간(Scale Space) 생성을 통해 크기 불변 속성 달성

(2)키포인트 검출

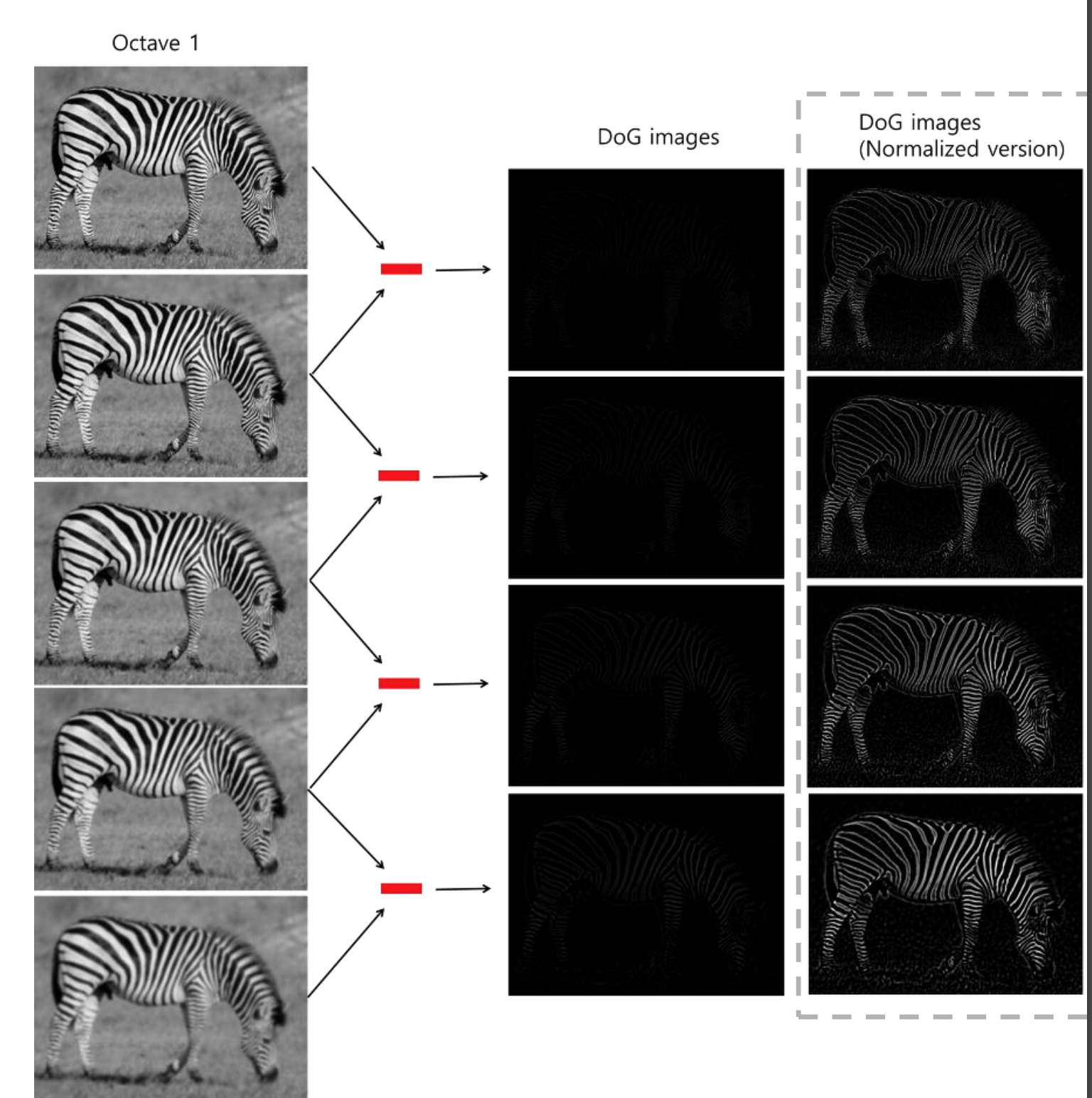
2-1) 키포인트 검출 시 DOG(Difference of Gaussian) 사용

두 사진의 차(Difference)로 경계선을 검출하는 방법
Log보다 Dog방식의 계산 효율성이 훨씬 좋음

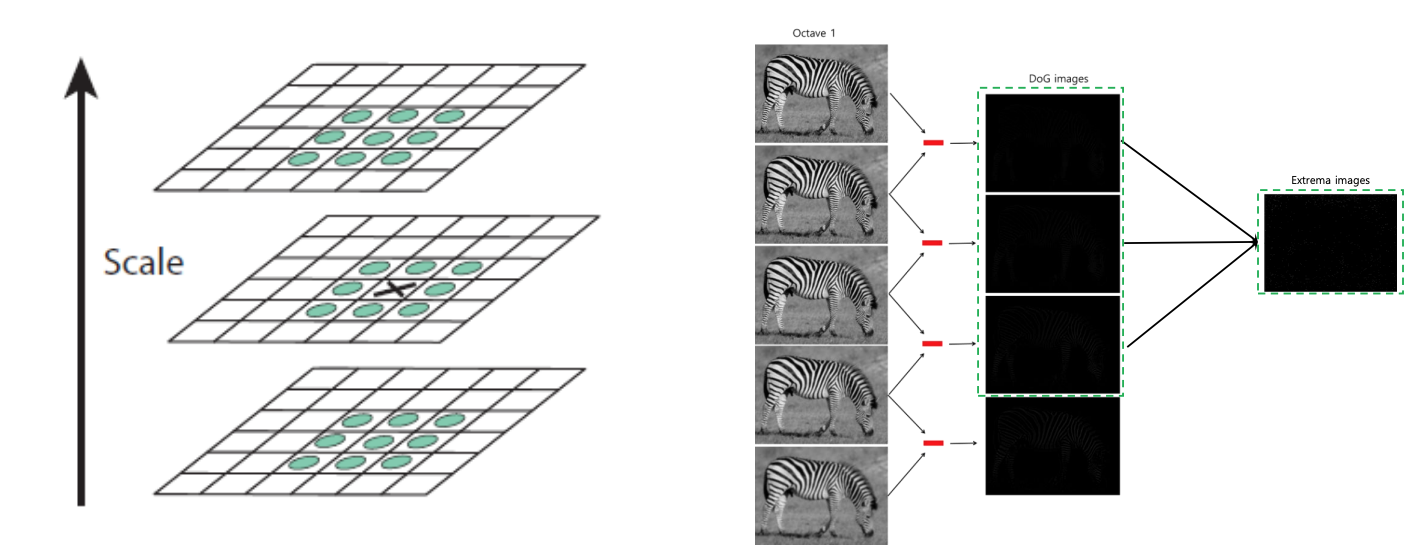
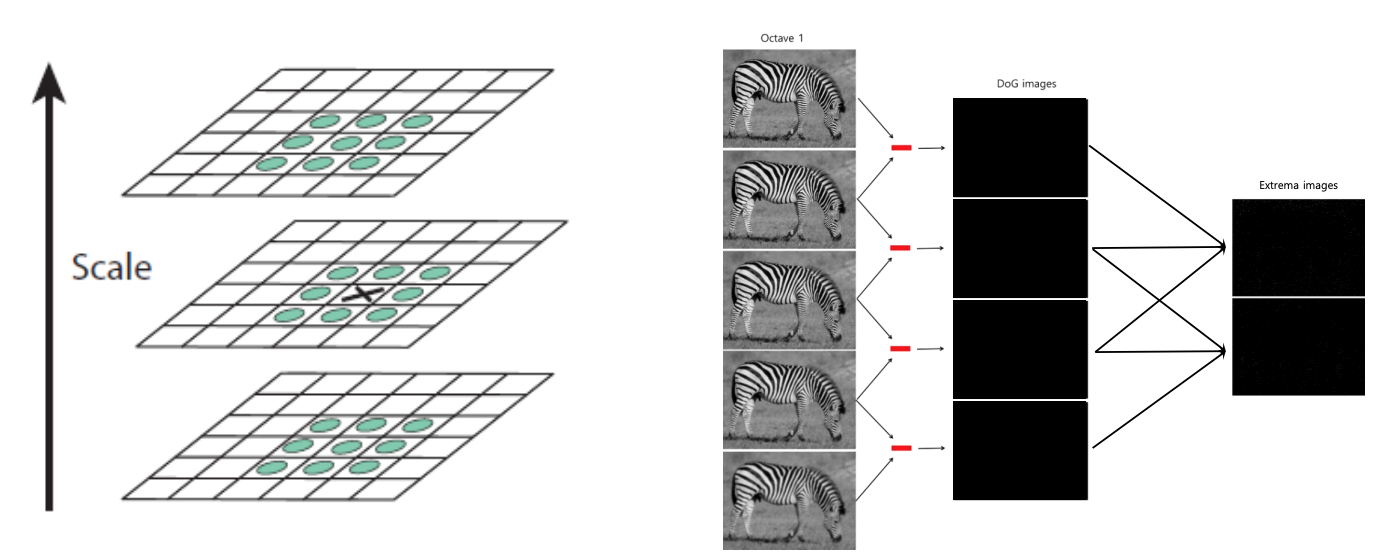
2-2) 키포인트 검출

DoG 영상에서 가장 아래, 가장 위 layer를 제외한 세 영상에 대해 모든 픽셀을 순회하면서 극점(extrema) 탐색
극점 탐색 과정

(3) 나쁜 keypoint 제거

극값으로 찾은 keypoint들 중 활용가치가 떨어지는 것은 제거
- a. contrast가 낮거나 -> 특정 임계값과 비교
- b. edge에 해당 -> Hessian 행렬의 특징 가능성 값을 기반으로 판단
최종 keypoints 검출

(4) keypoint에 방향(orientation) 할당

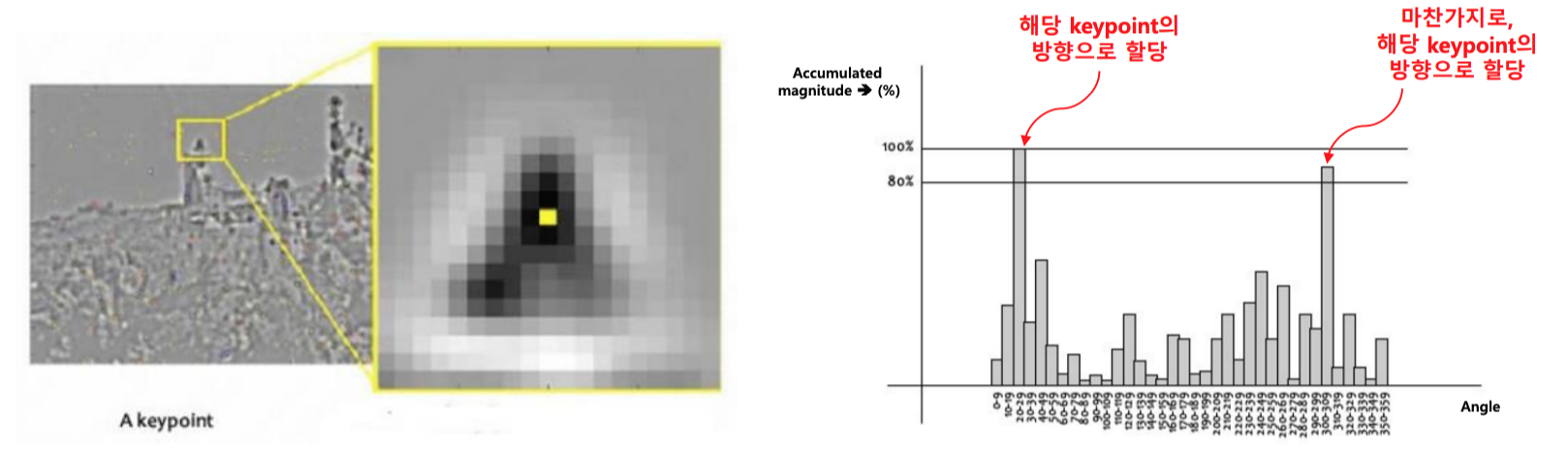
각 키포인트에 일정 크기의 윈도우를 씌운 후, 픽셀들의 gradient방향 히스토그램 생성->지배적인 방향 할당
회전 불변 속성 달성

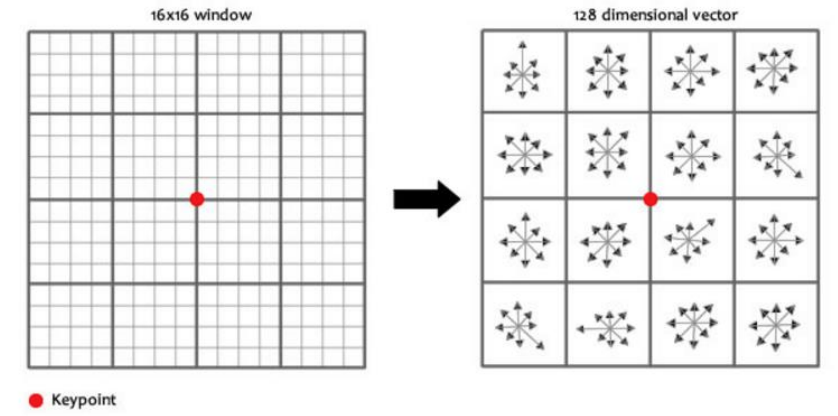
(5) 특징 기술자(descriptor) 생성

키포인트 주변 16x16 픽셀들의 그레디언트 히스토그램 계산

sub-block마다 8bin의 방향 히스토그램 계산
16x8=128 길이의 방향 히스토그램 생성
회전, 밝기 의존성 해결
- sub-block 방향 히스토그램에서 키포인트의 방향만틈 빼줌
- -> 키포인트 방향에 상대적으로 변함
- -> 일관된 방향 히스토그램 도출
- 즉 sub-block 내 밝기 정규화
128차원 특징 벡터(feature vector) 생성 -> 매칭 등에 활용

정규 라플라시안 맵 구축

[Mikolajczik2002a]의 실험 결과에 따르면, 정규 라플라시안이 가장 안정적으로 극점 형성
정규 라플라시안과 유사한 DOG 계산으로 대치
- DOG는 차 연산이므로 계산이 매우 빠름
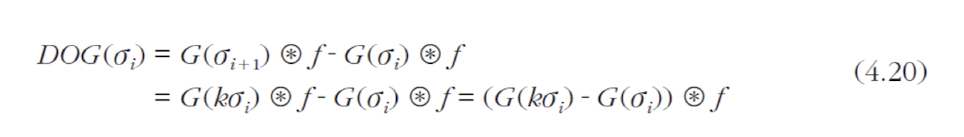
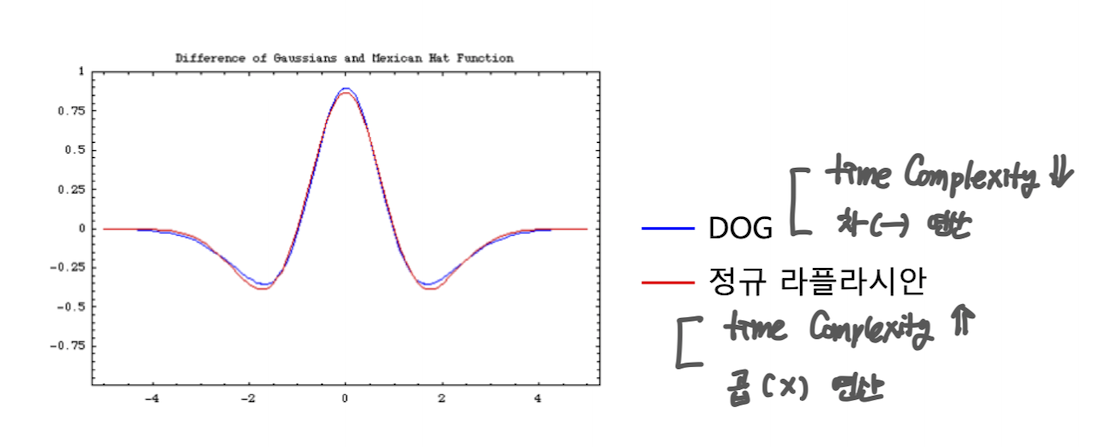
- DOG vs. Normalized laplacian

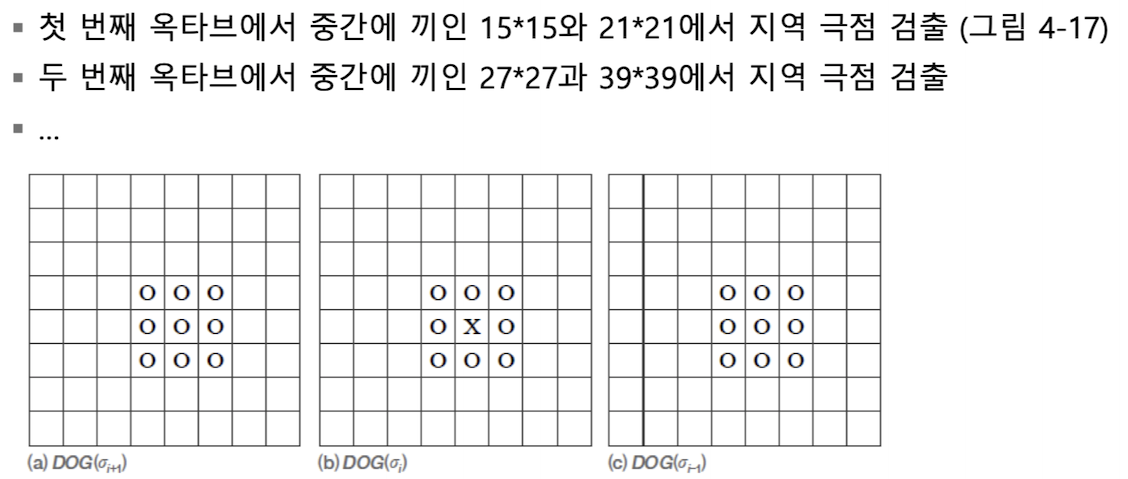
특징점(키포인트) 검출

한 옥타브에는 다섯 장의 DOG 영상
중간에 낀 세 장의 DOG 맵에서 극점 검출
- 주위 26개 이웃에 대해 최저 또는 최대인 점
- 9 x 3 = 27 -> 가운데 점 1개 뺀 값 -> 26개 이웃
검출된 극점을 키포인트(Key point)라고 부름
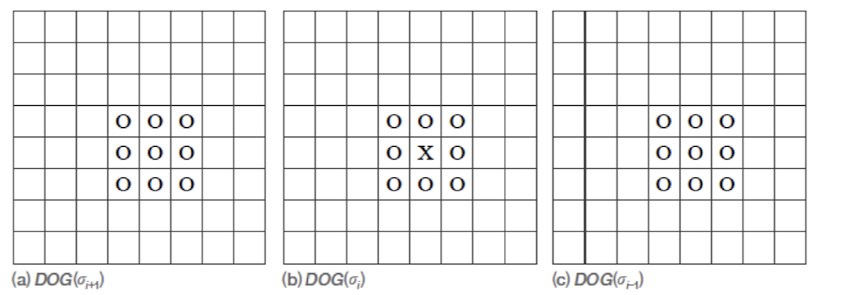
- DOG맵에서 키포인트(지역 극점) 검출

위치와 스케일 계산

키포인트는 <y,x,o,i> 정보를 가짐
옥타브 o의 i번째 DOG 영상의 (y,x)에서 검출
미세 조정(부분 화소 정밀도)을 거쳐 <y',x',o',i'> 로 변환됨
위치와 스케일 계산 식 적용

공개 소프트웨어

David Lowe
Rob Hess
Andrea Vedaldi
OpenCV

4.4 SURF 검출

SURF(Speeded up robust feature)

반복률 희생 없이 SIFT보다 빠른 알고리즘 추구
성능 개선 요인
- Log(DoG)대신 Hessian 행렬 사용
- 행렬식 근사 계산
- 적분 영상(integral image)사용
- 스케일 공간 생성 시 가우시안 스무딩 대신 근사 연산자 사용
헤시안의 행렬식 이용
- 헤시안의 행렬(Hessian Metrix)이란?
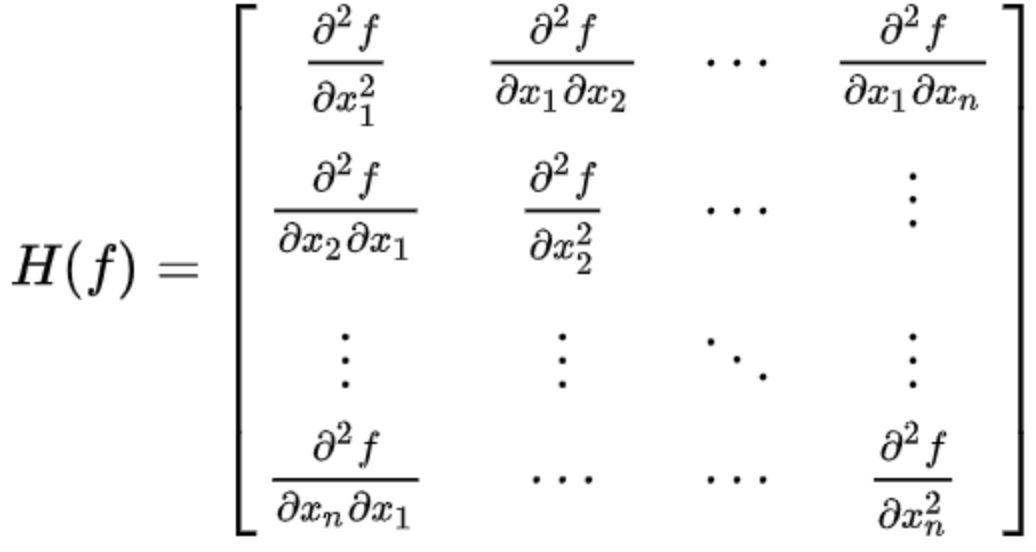
  - 각각 행과 열의 번호를 갖는 변수들로 미분한것을 모아놓은 식으로,
  - 임계점이 존재하는 경우 해당 임계점에서
    - 해시안 행렬의 고유값들이 모두 양수면 극소점,
    - 해시안 행렬의 고유값들이 모두 음수면 극대점,
    - 둘 다 있으면, 안장점에 해당한다(안장점: 변수가 2개 이상인 함수에서 보는 방향에 따라 극소점/극대점으로 보이는 지점)
행렬식을 빠르게 계산하기 위해 $d_{yy}, d_{xx}, d_{yx}$를 9*9 마스크로 근사 계산
- 마스크 계산은 적분 영상 이용
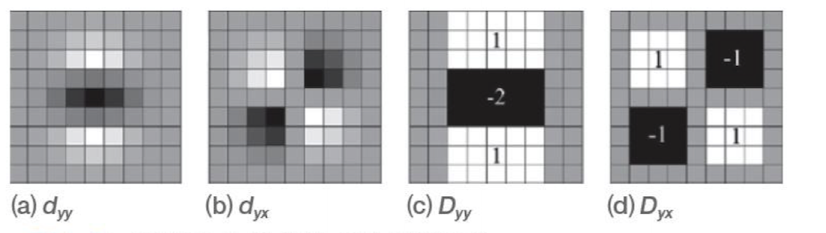
- 가우시안 두 번 미분한 연산자(회색은 0)
- 0~1사이의 실수값을 계산할 경우 float 연산이므로 속도가 매우 느림 -> 0/1 정수 계산이 필요

SURF의 스케일 공간

원본 영상은 그대로 둔 채 다중 스케일 마스크 적용
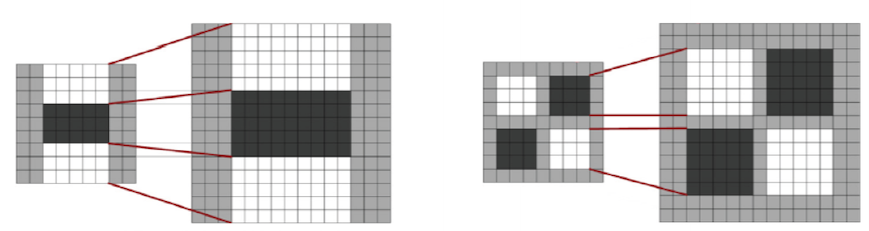
- 다음 스케일의 연산자로 확장

SURF의 옥타브 구성

SIFT vs. SURF

SIFT
- 단일 스케일 연산자를 다중 스케일에 적용
SURF
- 단일 스케일 영상에 다중 스케일 연산자를 적용, 즉 원본영상은 그대로 둔채 마스크를 바꿔가면서 계산
- 마스크를 근사 계산하면서 시간복잡도를 낮춤

지역 극점 검출(Pass)

SURF의 속도 개선 보고[Bay2008]

800*640영상에서 SURF 70ms, SIFT 400ms, 해리스 라플라스 2100ms
SURF > SIFT > 해리스 라플라스 순으로 빠름

4.5 지역 특징 검출 알고리즘의 특성 비교

튜토리얼 논문

Local Invariant Feature Detectors, Tinne Tuytelaars1 and Krystian Mikolajczyk, 2007

성능 분석 논문

Evaluation of interest point detectors, Cordelia Schmid, Roger Mohr, Christian Bauckhage, 2005
A Comparison of Affine Region Detectors, Krystian Mikolajczyk , Tinne Tuytelaars, 2005
Evaluation of local detectors and descriptors for fast feature matching, O Miksik, 2012
Interesting Interest Points, Henrik Aanæs, 2012

어떤 지역 특징을 선택해야 하나?

손수 성능 실험을 수행하고 판단
[Tuytelaars 2007, 7.1절]의 지침 참조

'인공지능(AI) > 컴퓨터비전(CV)' 카테고리의 다른 글

[패턴인식] 영상분할(2): 민시프트, 대화식 물체 분할 (0)	2021.12.16
[패턴인식] 영상분할(1): 영상 분할의 원리, 전통적 방법 (0)	2021.12.16
[패턴인식] 지역 특징 검출(1): 이동/회전 불변 특징점 검출, 위치 찾기 알고리즘 (0)	2021.10.24
[패턴인식] 에지 검출(2) : 캐니 에지, 컬러 에지, 선분 검출 (0)	2021.10.24
[패턴인식] 에지 검출(1) : 에지 검출의 기초, 영교차 이론 (0)	2021.10.24