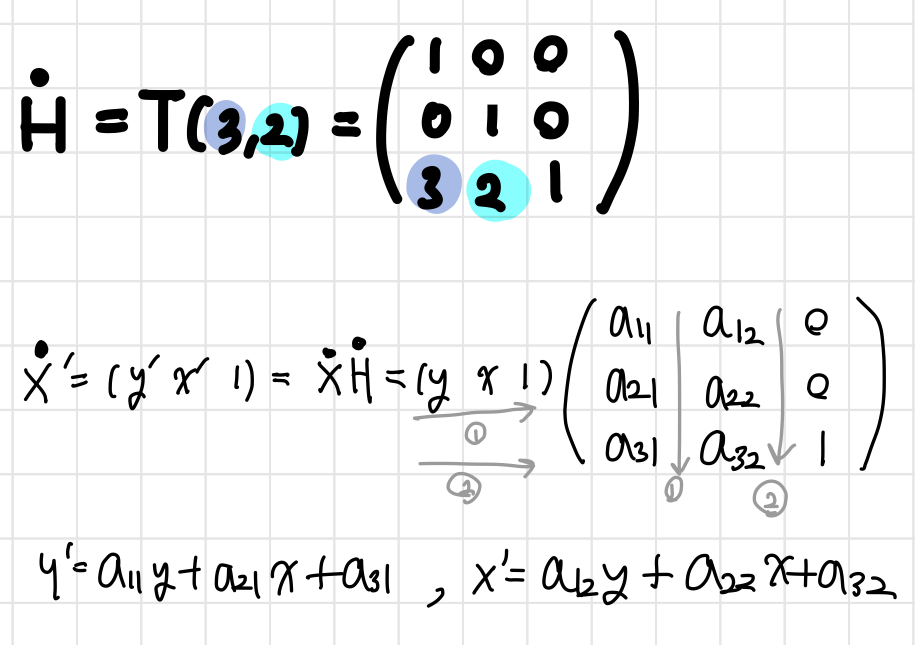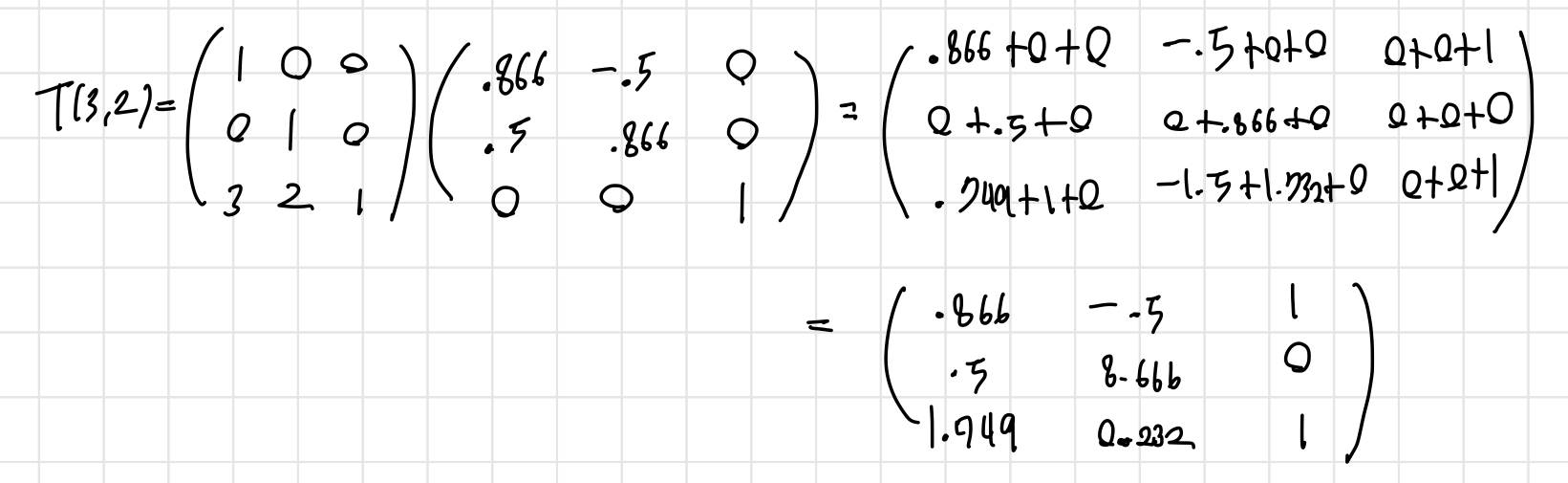Digital Image Processing
목차
0. Preview
1. 디지털 영상이란?
2. 히스토그램
3. 이진 영상
4. 영상 처리의 세가지 기본 연산
5. 다해상도
6. 모폴로지
7. 컬러
<0~2.히스토그램>은 이전 게시글을 참고해주세요
https://codingsmu.tistory.com/102
[패턴인식] 영상 처리(1) : 디지털 영상, 히스토그램
Digital Image Processing 목차 0. Preview 1. 디지털 영상이란? 2. 히스토그램 3. 이진 영상 4. 영상 처리의 세가지 기본 연산 5. 다해상도 6. 모폴로지 7. 컬러 0. Preview 영상처리(DIP, Digital Image Process..
codingsmu.tistory.com
3. 이진 영상
3.1 이진화와 오츄 알고리즘
이진화
- 명암영상을 흑(0)과 백(1)만 가진 이진 영상으로 변환
- $b(j,i)$
- $= 1, f(j,i) >= T$
- $ = 0, f(j,i) < T$
임계값 방법
- 두 봉오리 사이의 계곡을 임계값 T로 결정(-> Bimodal)
- 이진화 임계치 자동결정(by Gonzales & Woods)

Image의 Bimodal
- 자연영상에서는 계곡 지점 결정이 어려움
-
이진화
-
오츄 알고리즘[Ostsu79]
- 이진화시, 흑 그룹(black groun)과 백 그룹(white group) 각각이 균일할수록 좋다는 원리에 근거
- 균일성은 분산으로 측정($분산 \propto \frac{1}{균일성}$)
- 균일성이 클수록 t에 높은 점수를 주며, 가능한 t에 대해 점수를 계산 후 가장 좋은 t를 최종 임계값으로 취함
- 분산의 가중치 합 $v_{within}(.)$을 목적함수로 이용한 최적화 알고리즘
- 목적함수(Objective function), 혹은 비용함수(Cost function)은 분산을 사용함
- 분산이 작을수록 균일성이 크므로 목적함수(분산의 가중치 합) 값이 작을수록 점수가 높다
- $T = argminV_{within}(t)$, $t \in [0,1,...,L-1]$

- 목적함수: $V_{within}(t)$로, 두 분산의 가중치의 합으로 정의
- $w_0(t), w_1(t)$ 는 임계값 t에 따라 생성된 흑 화소와 백 화소 집합의 크기로서 가중치 역할
- $v_0(t), v_1(t)$ 는 두 집합의 분산이며 $\mu$는 평균값
- 위의 계산의 경우 W, V 두개를 각 L번 계산을 하게 되므로 시간복잡도는 $O(L^2)$을 가지게 된다
- $\mu, v$는 주어진 영상에 대해 한 번만 계산하면 되기 때문에 상수로 간주 가능
- $\mu = \sum_{i=0}^{L-1}i\hat{h}(i)$
- $v = \sum_{i=0}^{L-1}(i-\mu)^2\hat{h}(i)$
- 즉, $v = w_0(t)(1-w_0(t))(\mu_0(t) - \mu_1(t))^2 + v_{within}(t) = v_{between}(t)+v_{within}(t)$이다
- 이때, v는 상수이므로 $v_{within}(t)$을 최소화 하는 것은 $v_{between}(t)$을 최대화하는 것과 같다
- 따라서 최대화 문제를 $T = argmax V_{between}(t)$, $t \in [0,1,...,L-1]$로 바꿀 수 있다
- 여기서 $v_{between}(t) = w_0(t)(1-w_0(t))(\mu_0(t) - \mu_1(t))^2$이다
- t-1번째의 계산 결과를 t번째에 활용하여 빠르게 계산
- 초기값(t = 0) : $w_0(0) = \hat{h}(0), \mu_0(0) = 0$
- 순환식(t > 0)
- $w_0(t) = w_0(t-1) + \hat{h}(t)$
- $\mu_0(t) = \frac{w_0(t-1)+\mu_0(t-1)+t\hat{h}(t)}{w_0(t)}$
- $\mu_1(t) = \frac{\mu+w_0(t)\mu_0(t)}{1-w_0(t)}$
오츄 알고리즘(효율적인 버전)
- input : 영상 $f(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1$
- output: 이진영상 $b(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1$
- 코드는 아래 더보기를 눌러주세요
오츄 알고리즘 코드
# hat_h is a normal histogram of image f
w_0 = [0] * L
mu_0 = [0] * L
mu_0 = [0] * L
v_between = [0] * L
b = [[0]*N for _ in range(M)]
# when t = 0, initialization value
w_0[0] = hat_h[0]
mu_0[0] = 0
mu = 0
for i in range(L):
mu += i*hat_h[i]
for t in range(1,L):
#when t > 0, recursion eqaution
w_0[t] = w_0[t-1] + hat_h[t]
mu_0[t] = ((w_0[t-1]*mu_0[t-1]) + t*hat_h[t]) / (w_0[t])
mu_1[t] = (mu-w_0[t]*mu_0[t]) / (1-w_0[t])
# calculate v_between[t]
v_between[t] = w_0[t]*(1-w_0[t])*((mu_0[t]-mu_1[t])**2)
# the maximum value in v_between[] is critical value T
T = max(v_between)
# image binarization
for j in range(M):
for i in range(N):
if f[j][i] >= T: # white
b[j][i] = 1
else: # black
b[j][i]= 0
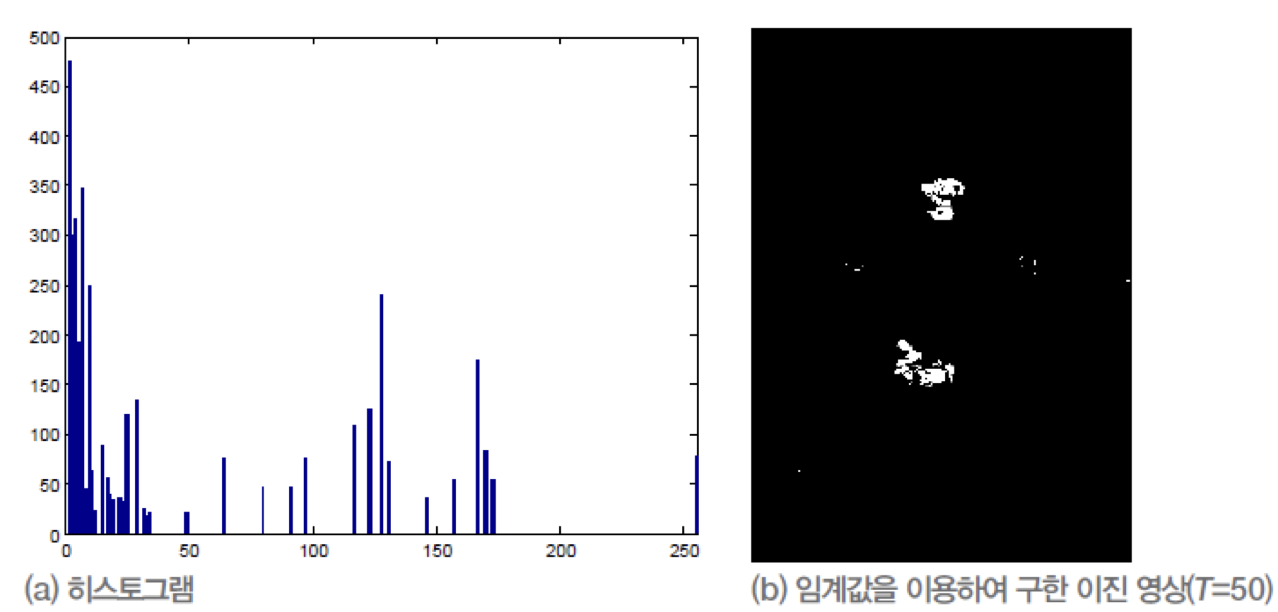
오츄 알고리즘으로 이진화한 영상 예시

- 오츄 알고리즘을 적용하기 좋은 영상은 히스토그램으로 나타냈을 때 계곡/전경, 즉 이진적으로 나누어지는 영상이 좋음
- (a),(t)는 오츄알고리즘을 적용하기 좋은 사진, (b)는 좋지 않은 사진임
3.2 연결요소
화소의 모양과 연결성

연결요소 번호 붙이기
- Component Labeling : 이진 영상을 덩어리진 컴포넌트 별로 독립된 레이블을 부여
- Input Image, 1: 전경, 0: 배경

Input Image
- 4-연결성 (4-connectivity), 8 연결성(8-connectivity)

연결요소 번호 붙이기
범람 채움
- 스택오버플로우(stack overflow) 위험
- 함수가 종료되기전 계속 호출되므로, 메모리에 계속 누적되어 스택오버플로우 발생 가능성 높음
- 고해상도 이미지에서 발생 위험 증가
- 범람 채움(4-연결성 버전)
- input : 이진영상 $b(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1$
- output: 이진영상 $l(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1$
- 코드는 아래 더보기를 눌러주세요
4-연결성 코드
# copy b to I : 0 -> 0, 1 -> -1(unnumbering)
I = [[-1]*N for _ in range(M)]
for j in range(M):
for j in range(N):
if b[j][i] == 0:
I[j][i] = 0
# boundary of I, set the 0 into pixel that j=0,j=M-1,i=0,i=N-1
for j in range(M):
if j == 0 or j == M-1:
map[j] = [0]*N
continue
map[j][0] = 0
map[j][-1] = 0
label = 1
for j in range(1, M-1):
for i in range(1, N-1):
if I(j,i) == -1:
flood_fill4(I, j, i, label)
label += 1
def flood_fill4(I, j, i, label):
if I(j,i) == -1:
flood_fill4(I, j, i+1, label) #east
flood_fill4(I, j, i-1, label) #west
flood_fill4(I, j+1, i, label) #south
flood_fill4(I, j-1, i, label) #north
4. 영상 처리의 세가지 기본 연산
4.1 점 연산(Pixel, 통계적 연산)
- 점 연산이란? 오직 자신의 명암값에 따라 새로운 값을 결정
- 식으로 표현하면 아래와 같다
- 대부분은 k=1 (즉, 한 장의 영상을 변환)이며, t는 픽셀 단위로 처리하는 연산임
- $f_{out}= t(f_1(j,i), f_2(j,i), ...., f_k(j,i))$
선형 연산 예시(k=1) + Clipping(over/underflow 방지)
- $f_{out}= t(f(j,i))$
- = $min(f(j,i) + a, L-1)$, (밝게)
- 두 번째 인자는 첫번째 인자가 L이상 시, overflow이므로 이를 방지하기 위한 상수값(Clipping)
- = $max(f(j,i) - a, 0)$, (밝게)
- 두 번재 인자는 첫번째 인자가 0 미만 시, underflow이므로 이를 방지하기 위한 상수값(Clipping)
- = $(L-1) - f(j,i)$, (반전)
- = $min(f(j,i) + a, L-1)$, (밝게)

여러가지 선형 점 연산
비선형 연산 예시
- 감마 수정(모니터나 프린터 색상 조절에 사용)
- $f_{out} = (L-1)*(\hat{f}(j,i))^{\gamma}$
- 이때 $\hat{f}(j,i) = \frac{f(j,i)}{(L-1)}$
- 위 연산은, L=266일 때, 0~255사이의 값을 0~1 값으로 정규화(normalize)해주는 계산임
- 즉, $\gamma$ 값이 커짐에 따라 제곱되는 수는 0~1사이의 값이므로 $f_{out}$은 어두워진다

감마 수정
디졸브(dissolve) 예시
- 디졸브란? 두 장의 영상(k = 2)을 Weighted Sum 하는 것으로 선형 연산에 해당
- $f_{out} = \alpha f_1(j,i) + (1-\alpha)f_2(j,i)$로, 여기서 $\alpha$는 가중치(weight)에 해당

디졸브 효과
4.2 영역 연산(Region : Convolution)
- 영역 연산이란? 이웃 화소의 명암값에 따라 새로운 값 결정
- 상관(Correlation)
- 원시적인 매칭 연산(물체를 윈도우 형태로 표현하고 물체를 검출)
- 수식
- 1차원: $g(i) = u x f = \sum_{x=-(w-1)/2}^{(w-1)/2}u(x)f(i+x)$
- 2차원: $g(i) = u x f = \sum_{y=-(h-1)/2}^{(h-1)/2}\sum_{x=-(w-1)/2}^{(w-1)/2}u(y,x)f(i+y,i+x)$
- 2차원 상관 예시
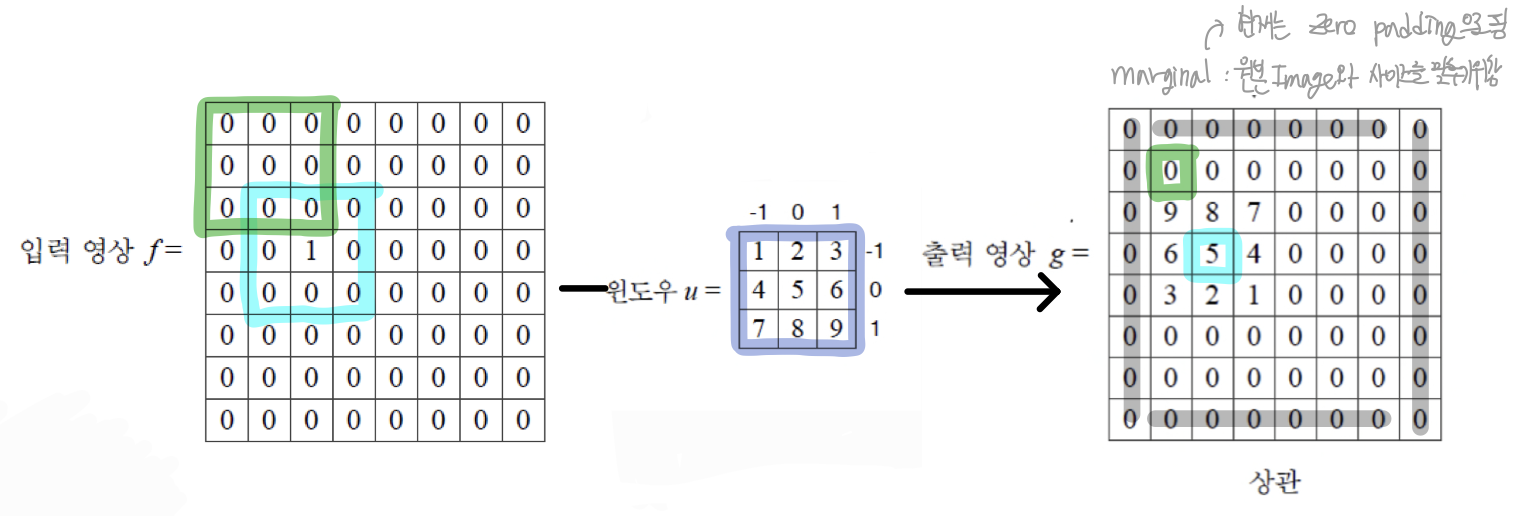
컨볼루션(Convolution)
- 윈도우를 뒤집은 후 상관 적용, 선형 연산
- 수식
- 1차원: $g(i) = u * f = \sum_{j=-(w-1)/2}^{(w-1)/2}u(x)f(i-x)$
- 2차원: $g(i) = u * f = \sum_{y=-(h-1)/2}^{(h-1)/2}\sum_{x=-(w-1)/2}^{(w-1)/2}u(y,x)f(i-y,i-x)$
- 임펄스 반응(Impulse Response)

상관과 컨볼루션의 원리
컨볼루션 예제

다양한 마스크와 컨볼루션 효과
박스와 가우시안은 스무딩 효과
- 가우시안은 박스와 비슷하나 원본 화소유지가 더 잘됨
- 평활화(Smoothing), 평균(Average) 마스크(Mask)에 해당
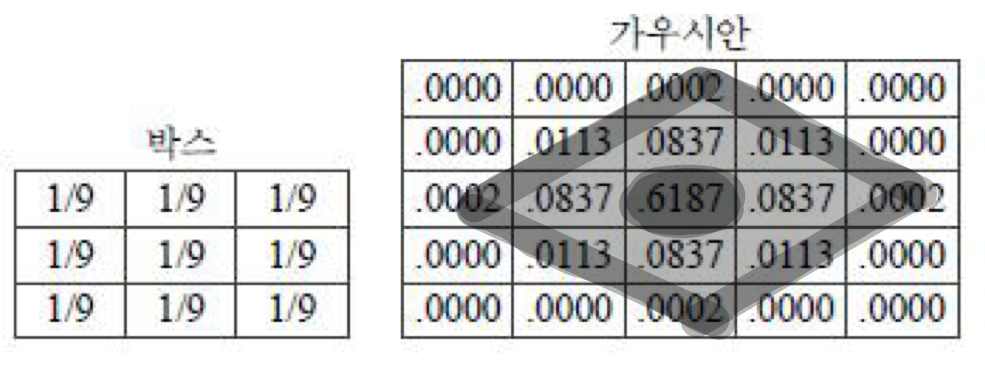
- 가우시안의 마름모로 색칠된 부분의 합은 1이 되어야 함(1초과일 경우 영상은 밝아지며,미만일 경우 어두워진다)
- 중심값(그림에서 0.6187)에서 멀어질수록 가중치(Weight)가 작아짐
- 샤프닝은 명암 대비 강조 효과
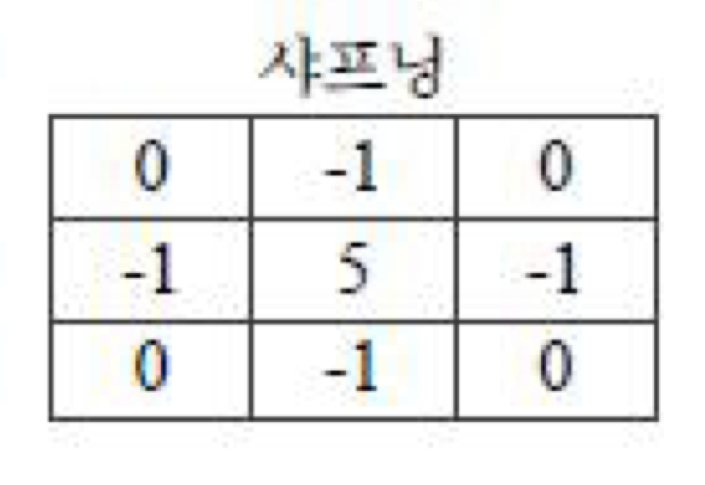
- 영상의 경계가 뚜렷해짐
- 수평 에지와 수직 에지는 에지 검출 효과

- 수평 에지는 수직방향으로 검출하여, 원본영상에서 수평(-)에 해당하는 에지를 검출하게 됨
- 수직 에지는 수평방향으로 검출하여, 원본영상에서 수직(|)에 해당하는 에지를 검출하게 됨
- 모션은 대각방향으로 블러(blur)처리가 이루어짐

- 대각 방향으로 값이 변함 -> 대각 방향으로 블러(blur)가 일어남
메디안 필터(Median Fileter) : 중간값 필터(!=Average)로 비선형 연산에 해당
- 솔트페퍼 잡음(Salt&Pepper Noise)에 효과적
- 메디안은 가우시안에 비해 에지 보존 효과가 뛰어남

4.3 기하 연산(Geometric Transform)
- 기하 연산이란? 일정한 기하 연산으로 결정된 화소의 명암값에 따라 새로운 값 결정
- 데이터 증강(data augmentation) 기법에 사용됨
동차 좌표와 동차 행렬
- 동차 좌표(Homogeneous Coordinate)
- $\dot{x} = (y,x,1)$
- ex:) (3,5) -> (3,5,1), (6,10,2), (0.3,0.5,0.1), ...
- 동차 행렬(Homogeneous Matrix) : $\dot{H}$
- 이동(Translation)
- $T(t_y,t_x)=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ t_y & t_x & 1 \end{pmatrix}$
- y방향으로 $t_y$, x방향으로 $t_x$만큼 이동
- 회전(Rotation)
- $R(\theta)=\begin{pmatrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix}$
- 원점을 중심으로 시계방향으로 $\theta$만큼 회전
- openCV관련 주의점(아래 더보기를 클릭하세요)
- 더보기

- 크기(Scaling)
- $S(s_y,s_x)=\begin{pmatrix} s_y & 0 & 0 \\ 0 & s_x & 0 \\ 0 & 0 & 1 \end{pmatrix}$
- y방향으로 $s_y$, x방향으로 $s_x$만큼 확대
- 기울림(Shearing)
- $Sh_y(h_y)=\begin{pmatrix} 1 & 0 & 0 \\ h_y & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$,
- $Sh_x(h_x)=\begin{pmatrix} 1 & h_x & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$
- $Sh_y$ : y 방향으로 $h_y$만큼 기울기
- $Sh_x$ : x 방향으로 $h_x$만큼 기울기
- 이동(Translation)
동차행렬을 이용한 기하 변환
- 예1: 어떤 점을 y방향으로 3, x방향으로 2만큼 이동시키는 동차 행렬 $\dot{H}$는 다음과 같다
- 예2: 아래 삼각형을 y방향으로 3, x방향으로 2만큼 이동시킨 후 30도 회전시켜보자

- 이동변환 T(3,2)후 $\dot{x_1},\dot{x_2},\dot{x_3}$ 구하기(아래 접은글 참고)
- 위 계산 결과 $\dot{x_1}=(6,7),\dot{x_2}=(5,7),\dot{x_3}=(6,10)로 이동$

- 회전 R(30도) 후 $\dot{x_1},\dot{x_2},\dot{x_3}$ 구하기(아래 접은글 참고)
-
더보기

- 그림에서 x2" = (7.83 3.562 1), 변환된 x3는 (6 10 1)로 x3" = (9.196 5.66 1) 계산 결과 정정하겠습니다 :)
-
- 위 계산 결과 $\dot{x_1}=(8.696, 3.062),\dot{x_2}=(4.83 ,3.562),\dot{x_3}=(6.598, 5.428)로 이동$

왜 동차 좌표를 사용하나?
- 복합 변환을 이용한 계산 효율
- 이동 후 회전은 두번의 행렬 곱셈, 하지만 복합 변환을 이용하면 한 번의 곱셈
- 위의 예제에서 변환에 필요한 행렬 T(3,2)와 R(30도)를 곱해 세 꼭지점에 각각에 대해 적용할 수 있다
- 즉, 행렬 곱을 두 번 한 것과 결과는 동일하지만 한 번의 곱셈으로 이동과 동시에 회전을 진행할 수 있다
- 계산은 아래 접은 글 참고
- 임의의 점 $(C_y, C_x)$를 중심으로 회전하는 식은 다음과 같다
- $T(-C_y,-C_x)R(\theta)T(C_y,C_x)$
- 먼저 회전축으로 중심을 옮겨준 후, 세타만큼 회전을 진행. 이 후 다시 원래 중심(0,0)으로 옮겨줌
영상에 적용
전방 변환(Forward mapping)은 심한 에일리어싱(Aliasing) 현상
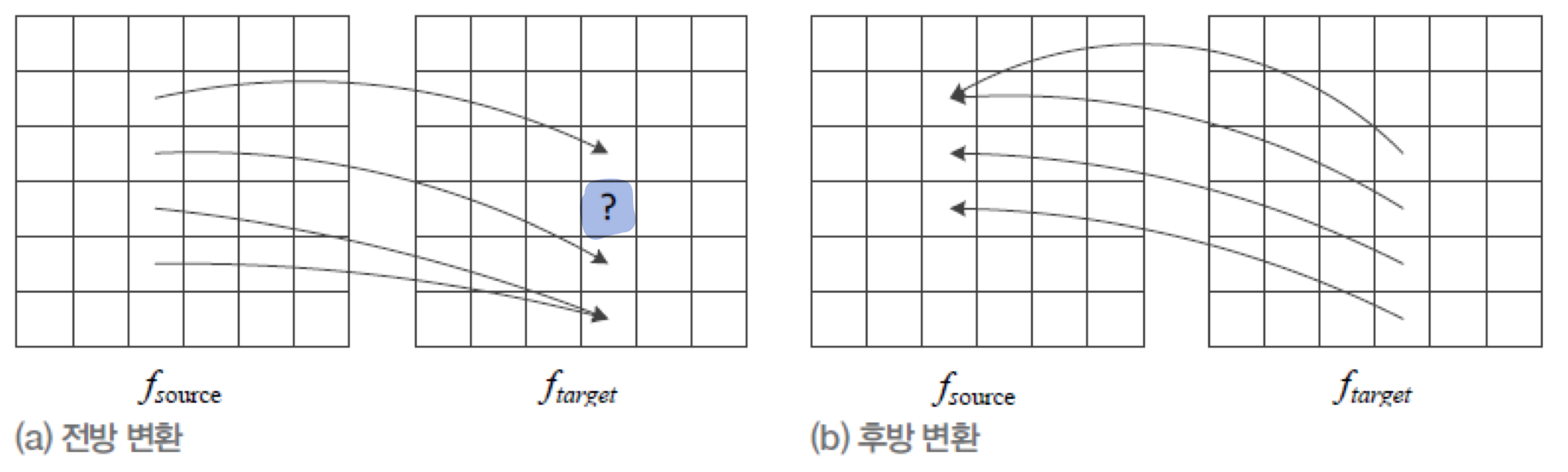
후방 기하 변환의 안티 에일리어싱 효과
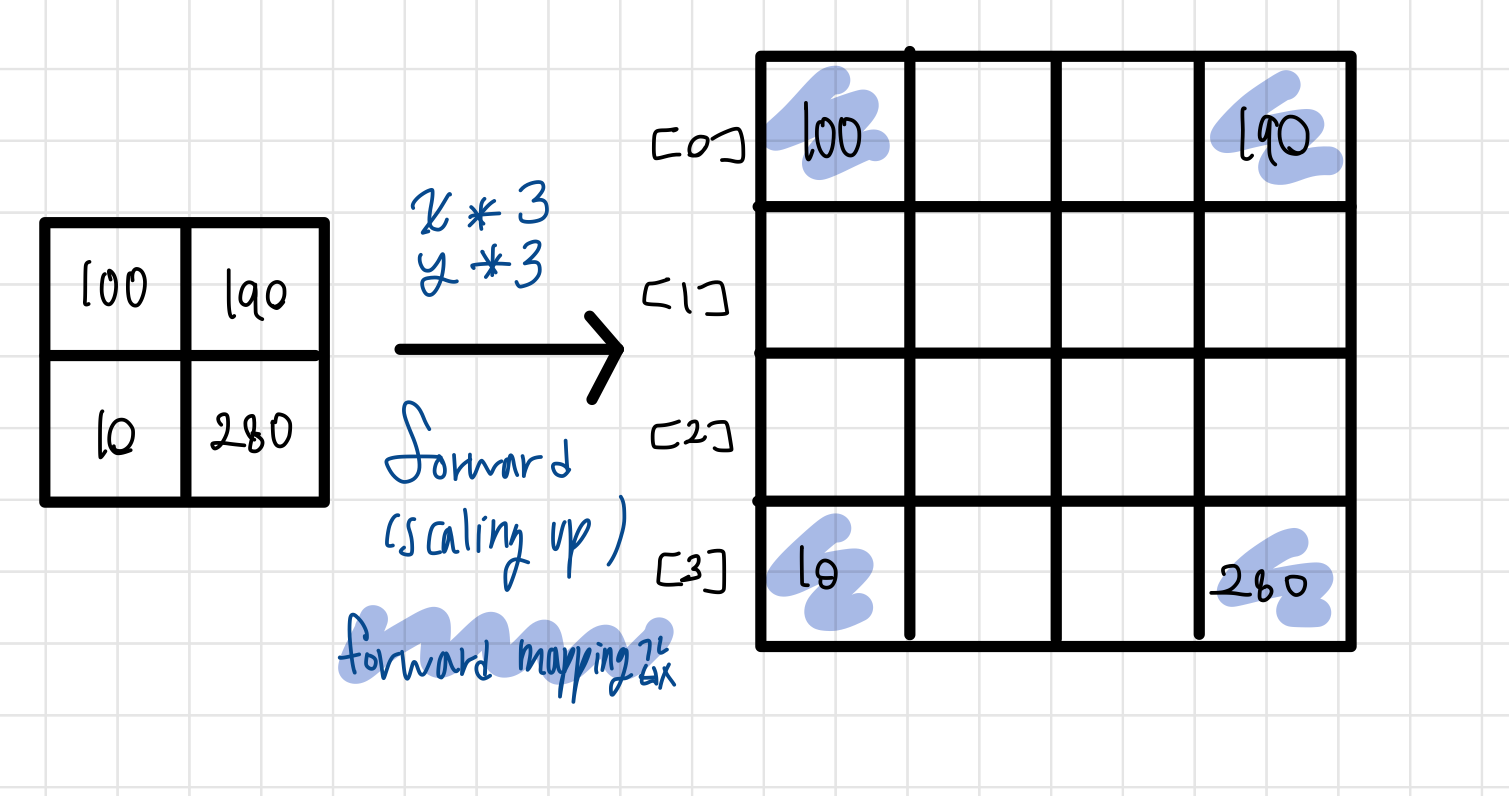
전방 변환 시, 매핑(mapping)이 되지 않는 홀(hole) 혹은 중첩(overlap)되는 픽셀이 생기는 문제점이 있음
- 전방기하변환 알고리즘
- 가로축으로 2만큼 Scaling up하는 연산이라고 가정
- input : 영상 $f_{source}(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1$, 변환 행렬 $\dot{H}$
- output: 기하변환된 영상 $f_{target}(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1$
- 코드는 아래 더보기를 눌러주세요
import numpy as np
# Scaling up to x*2, S(0,2)
s_y = 0, s_x = 2
S = [[s_y, 0, 0],[0, s_x, 0],[0, 0, 1]]
dot_H = np.array(S)
for j in range(M):
for i in range(N):
dot_x = np.array([j,i,1])
j1, i1, _ = dot_x@dot_H
# float to int
j1 = round(j1)
i1 = round(i1)
# ignore the spot outside the image space
f_target[j1,i1] = f_source[j,i]후방 변환(Backward mapping)을 이용한 안티 에일리어싱(Anti-Aliasing)
- 후반 변환 시, 홀과 중첩되는 픽셀이 생기지 않음
- 후방 기하 변환 알고리즘
- 가로축으로 2만큼 Scaling up하는 연산이라고 가정
- input : 영상 $f_{source}(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1$, 변환 행렬 $\dot{H}$
- output: 기하변환된 영상 $f_{target}(j,i)$, $0 <= j <= M-1, 0 <= i <= N-1
- 코드는 아래 더보기를 눌러주세요
import numpy as np
# Scaling up to x*1/2, S(0,1/2)
s_y = 0, s_x = 0.5
S = [[s_y, 0, 0],[0, s_x, 0],[0, 0, 1]]
dot_H = np.array(S)
for j in range(M):
for i in range(N):
dot_x = np.array([j,i,1])
j1, i1, _ = dot_x@dot_H
# float to int
j1 = round(j1)
i1 = round(i1)
# ignore the spot outside the image space
f_target[j,i] = f_source[j1,i1]보간에 의한 안티 에일리어싱(Anti-Aliasing by Interpolation)
- n을 계산할 때, n-1과 n+1 즉, 주변 화소를 이용하여 계산하는 방법

기하변환한 점의 좌표
선형 보간법(Linear Interpolation)

-
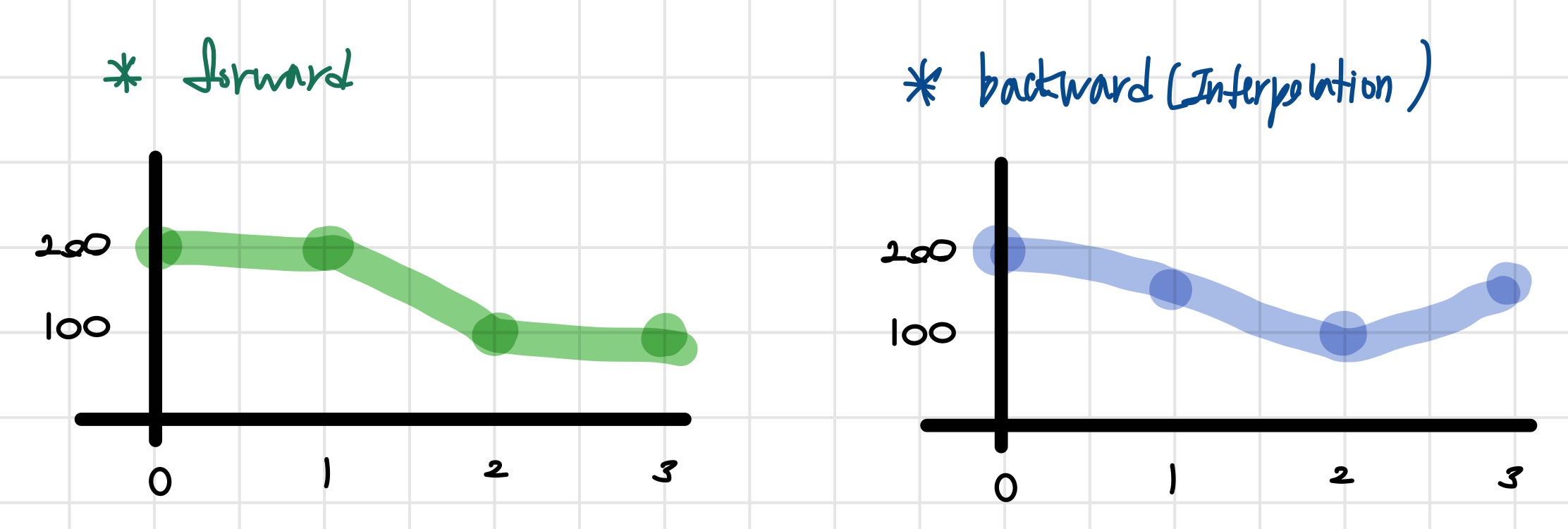
- Interpolation결과, Forward를 한 영상보다 더 부드럽게 값이 변경되는 것을 확인할 수 있다
양선형 보간법(Bi-Linear Interpolation)
- $f(\dot{x}) = (1-\alpha)f(x) + \alpha f(x+1)$

1차원에서 보간식 유도 - 예시
2차원에서 보간식 유도
- $f(y,\dot{x}) = (1-\alpha)f(y,x) + \alpha f(y,x+1)$
- $f(y+1,\dot{x}) = (1-\alpha)f(y+1,x) + \alpha f(y+1,x+1)$
- $f(\dot{y},\dot{x}) = (1-\beta)f(y,\dot{x}) + \beta f(y+1,\dot{x})$
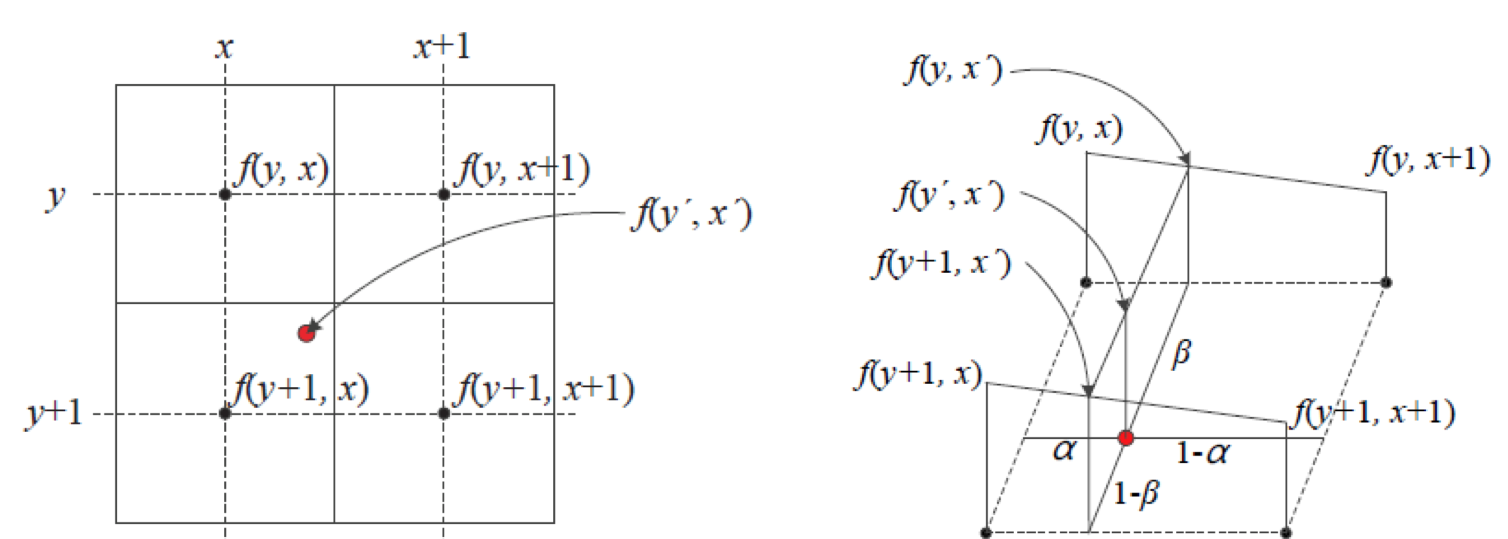
최근접 이웃, 양선형 보간, 양 3차 보간의 비교

영상 보간
<5. 다해상도 ~ >부터는 다음 게시글에서 계속...
https://codingsmu.tistory.com/104
[패턴인식] 영상 처리(3) : 다해상도, 모폴로지, 컬러
Digital Image Processing 목차 0. Preview 1. 디지털 영상이란? 2. 히스토그램 3. 이진 영상 4. 영상 처리의 세가지 기본 연산 5. 다해상도 6. 모폴로지 7. 컬러 은 이전 게시글을 참고해주세요 https://codingsm..
codingsmu.tistory.com
'인공지능(AI) > 컴퓨터비전(CV)' 카테고리의 다른 글
| [패턴인식] 에지 검출(1) : 에지 검출의 기초, 영교차 이론 (0) | 2021.10.24 |
|---|---|
| [패턴인식] 영상 처리(3) : 다해상도, 모폴로지, 컬러 (0) | 2021.10.24 |
| [패턴인식] 영상 처리(1) : 디지털 영상, 히스토그램 (0) | 2021.10.21 |
| [패턴인식] 컴퓨터 비전 소개 : Intro. Computer Vision (0) | 2021.10.17 |
| [논문리뷰] 적대적 생성 신경망 : Generative Adversarial Nets(GAN) (0) | 2020.09.17 |
![[패턴인식] 영상 처리(2) : 이진영상, 영상 처리의 세가지 기본 연산](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2F1Zcec%2FbtriAr8iPNv%2FAAAAAAAAAAAAAAAAAAAAAC-SWiboqRpuzfqM72LNCYx_iUhFXYkJLijFiTkEIKRT%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DKLsqognfImh4wCoGLB72trYdLn8%253D)