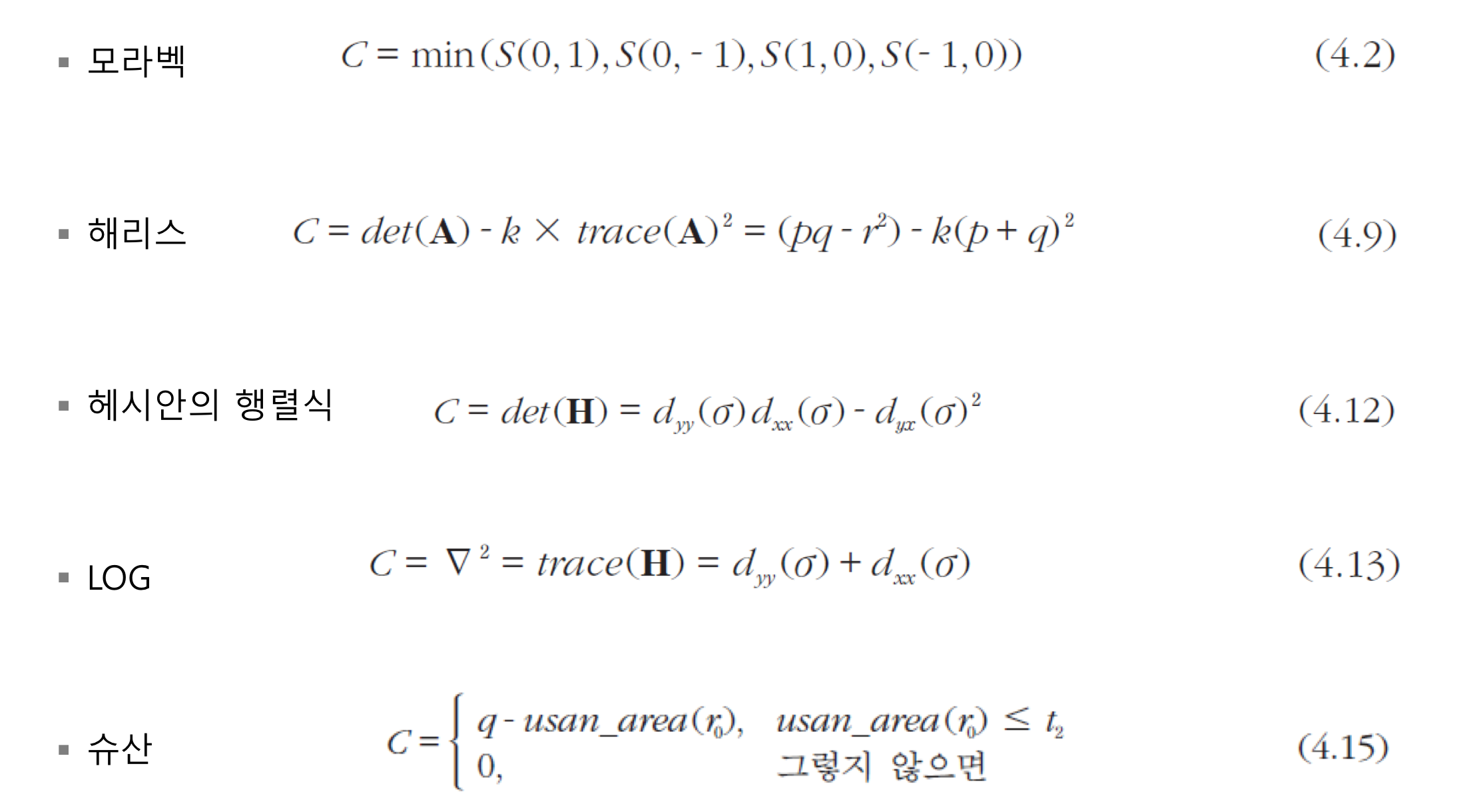반응형
Local Feature
목차
0. Preview
1. 지역 특징 검출의 기초
2. 이동과 회전에 불변한 특징점 검출
3. 위치 찾기 알고리즘
4. 스케일에 불변한 특징점 검출
0. Preview
- 대응점 찾기
- 같은 장면을 다른 시점에서 찍은 두 영상에서 대응(Correspond)하는 점의 쌍(Pair)을 찾는 문제
- 파노라마, 물체 인식/추적, 스테레오 등 컴퓨터 비전의 중요한 문제 해결의 단초

- 세 단계로 해결
1. 지역 특징 검출의 기초
1.1 특징 검출의 역사: 지역 특징의 대두
- 무엇을 특징점으로 쓸 것인가?
- 에지(Edge)는 강도와 방향 정보만 가지므로 매칭에 참여하기에 턱없이 부족
- 다른 곳과 두드러지게 달라 풍부한 정보 추출이 가능한 곳
- 에지 토막에서 곡률이 큰 지검을 코너로 검출(복잡)
- 코너 검출, dominant point 검출 들의 주제로 1980년대 왕성한 연구
- 90년대 소강 국면, 2000년대 사라짐
- 더 좋은 대안이 떠올랐기 때문
- 지역 특징이라는 새로운 물줄기(심플)
- 명암영상에서 직접 검출
- 의식전환: 코너의 물리적 의미(반복성)
- 에지 토막에서 곡률이 큰 지검을 코너로 검출(복잡)
1.2 지역 특징의 성질
- 지역특징
- <위치, 스케일, 방향, 특징 벡터> = ((y,x), s, $\theta$, x)로 표현
- 검출 단계 (4장) : 위치와 스케일 알아냄
- 기술단계 (6장) : 방향과 특징 벡터 알아냄
- 지역 특징이 만족해야할 특성
- 반복성, 분별력, 지역성, 정확성, 적당한 양, 계산 효율
- 이들 특성은 길항 관계로 응용에 따라 적절한 특징을 선택해야 함
1.3 지역 특징 검출 원리
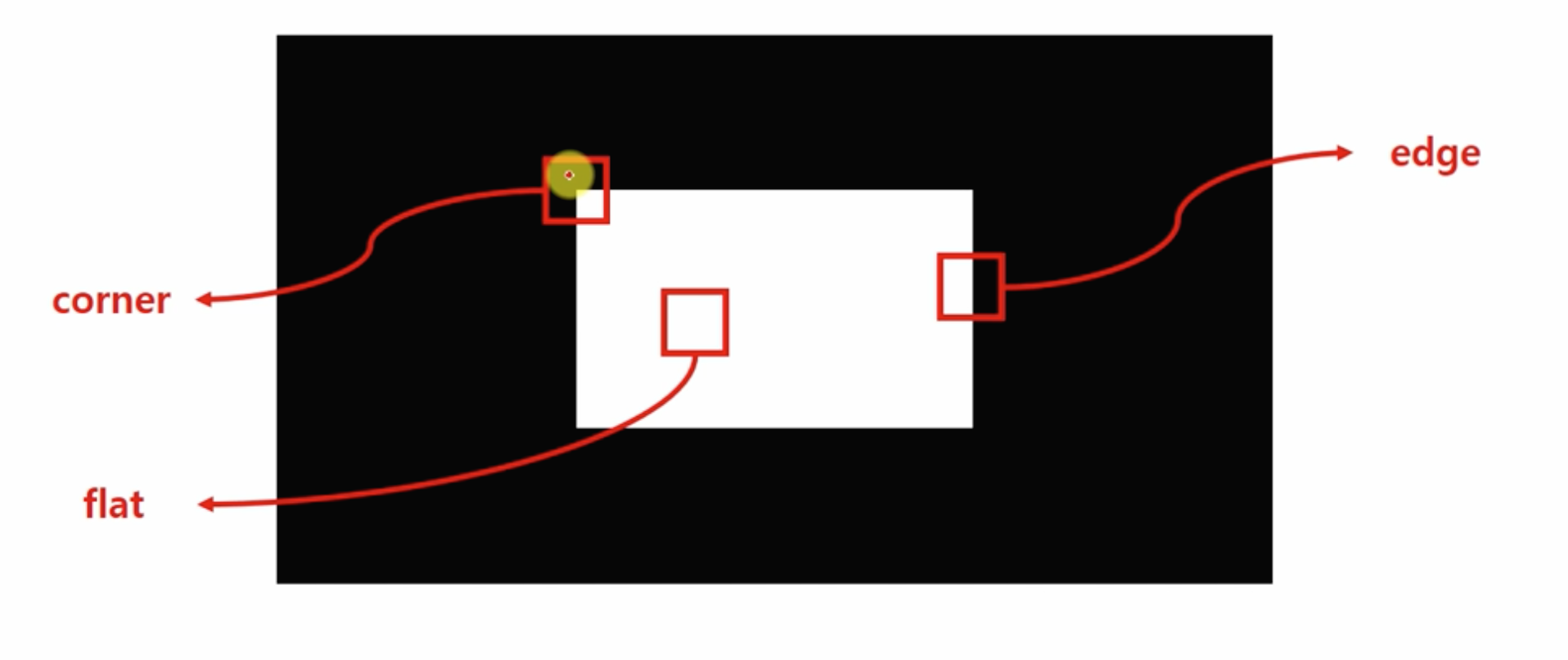
- 크게 세 종류의 영역으로 구분 가능
- 원리
- 인지 실험: 대응점을 찾기가 쉬운(좋은) 점은? 사람에게 쉬운 곳이 컴퓨터에게도 쉽다
- 좋은 정도를 수량화 하는 방법? 여러 방향으로 밝기 변화가 나타나는 곳일 수록 높은 점수
- 아래의 그림에서 지역 특징으로 유리한 정도는 a > b > c 순이다
-

2. 이동과 회전에 불편한 특징점 검출
2.1 모라벡 알고리즘 (Moravec Algorithm)
- 인지 실험에 주목한 모라벡[Moravec80]
- 제곱차의 합으로 밝기 변화 측정
- $S(v,u) = \sum_{y}\sum_{x}w(y,x)(f(y+v,x+u)-f(y,x))^2$
- 예제 : 제곱차 합 계산
- 아래의 삼각형을 가진 12x12 영상이 있다. 현재 조사하고 있는 점 (5,3)에 위치한 b, 마스크는 모든 값이 1인 3x3이라고 하자
- 이때 오른쪽으로 한 화소 만큼 이동시킨 S(0,1)을 계산해보자
- f는 입력 영상이고, w는 마스크이다($w(y,x) = 1( 4<=y<= 6 , 2 <= x <= 4), 0(그외))$

입력영상 f 
a, b, c위치에 따른 S(u,v) 맵 - a : 정방향으로 값이 크게 나옴 -> Local feature로 좋음
- b : 수직 방향으로 값이 크게 나옴 -> 특정 방향으로 큰 값을 가지면 해당 방향으로 edge를 가짐
- c : 주변 값이 모두 0으로 local feature로 좋지 않음
- 모라벡 함수 적용시 a(2), b(0), c(0)임
- 계산과정은 아래 참고
-
더보기

S(0,1) 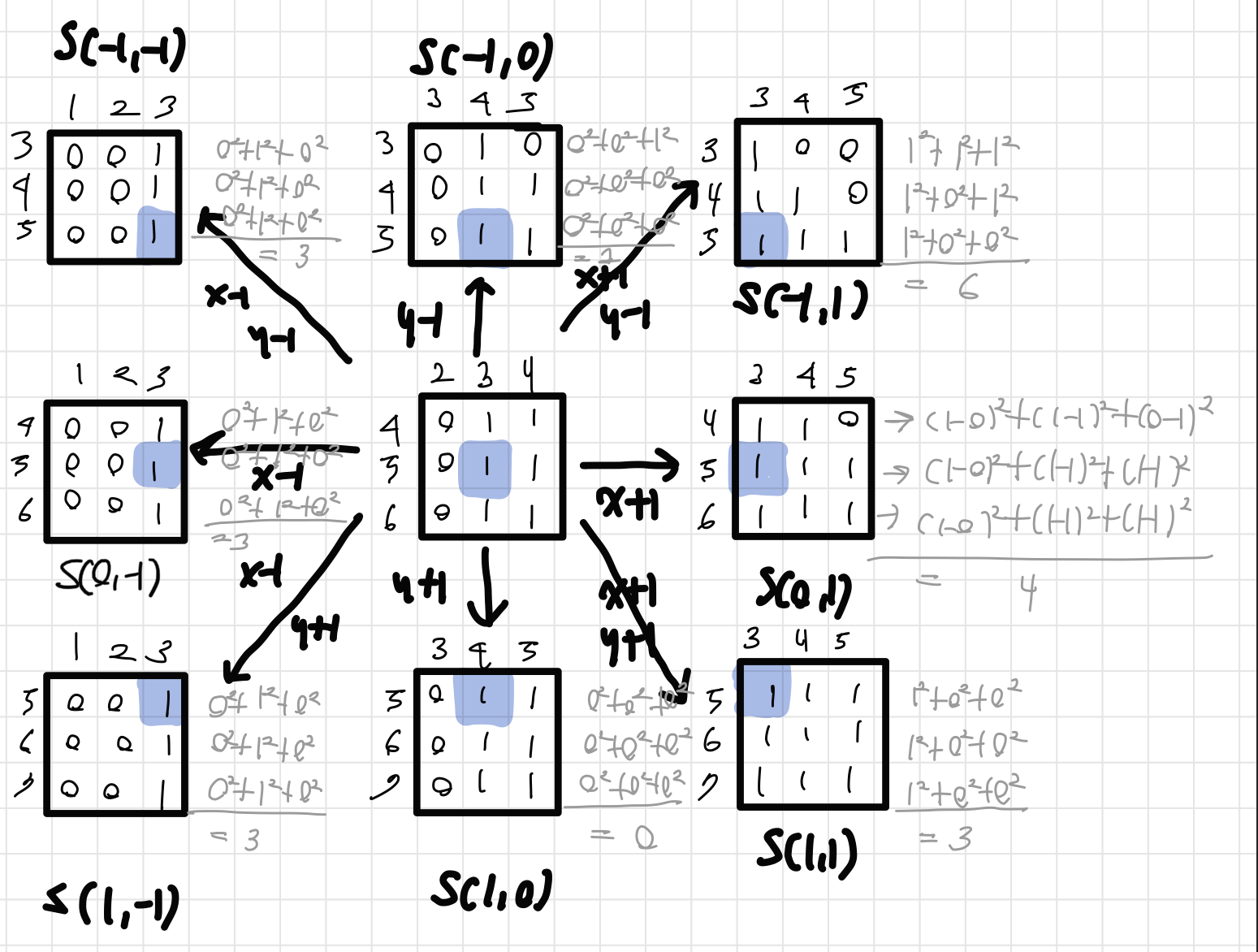
(5,3)을 S(0,0)일 때, 8-neighbor 계산
-
- 모라벡 알고리즘 적용 예시(9*9 마스크로 측정)

실제 영상에서 S맵(밝을수록 큰 값 [0:black~ 255:white] - S(.)맵을 관찰해 보면,
- a와 같은 코너에서는 모든 방향으로 변화가 심함
- b와 같은 에지에서는 에지 방향으로 변화 적지만, 에지에 수직 방향으로 변화가 심함
- c와 같은 곳은 모든 방향으로 변화 적음
- 따라서 a에 높은 값, c는 아주 낮은 값, b는 그 사이 값을 부여하는 함수를 만들면 됨
- 모라벡의 함수
- 특징 가능성 값 C
- $C = min(S(0,1), S(0,-1), S(1,0), S(-1,0)$
- 즉 4-연결성에서 min값 추출
- 한계
- 한 화소만큼 이동하여 네 방향만 봄
- 잡음에 대한 대처 방안이 없음
- 특징 가능성 값 C
2.2 해리스 코너
- 해리스의 접근[Harris88]
- 가중치 제곱차의 합을 이용한 잡음 대처로, 현재까지도 많이 사용하는 방식이다
- $S(v,u) = \sum_{y}\sum_{x}G(y,x)(f(y+v,x+u)-f(y,x))^2$
- 테일러 확장을 위 식에 대입해보자
- 테일러 확장: $f(y+v, x+u) =f(y,x) + vd_y(y,x) + ud_x(y,x)$
- 우변의 $f(y-x)$를 좌변으로 이항하면, $f(y+v, x+u) - f(y,x) = vd_y(y,x) + ud_x(y,x)$로 이를 대입하면,
- $S(v,u) = \sum_{y}\sum_{x}G(y,x)(f(y+v,x+u)-f(y,x))^2 = \sum_{y}\sum_{x}G(y,x)(vd_y(y,x) + ud_x(y,x))^2$

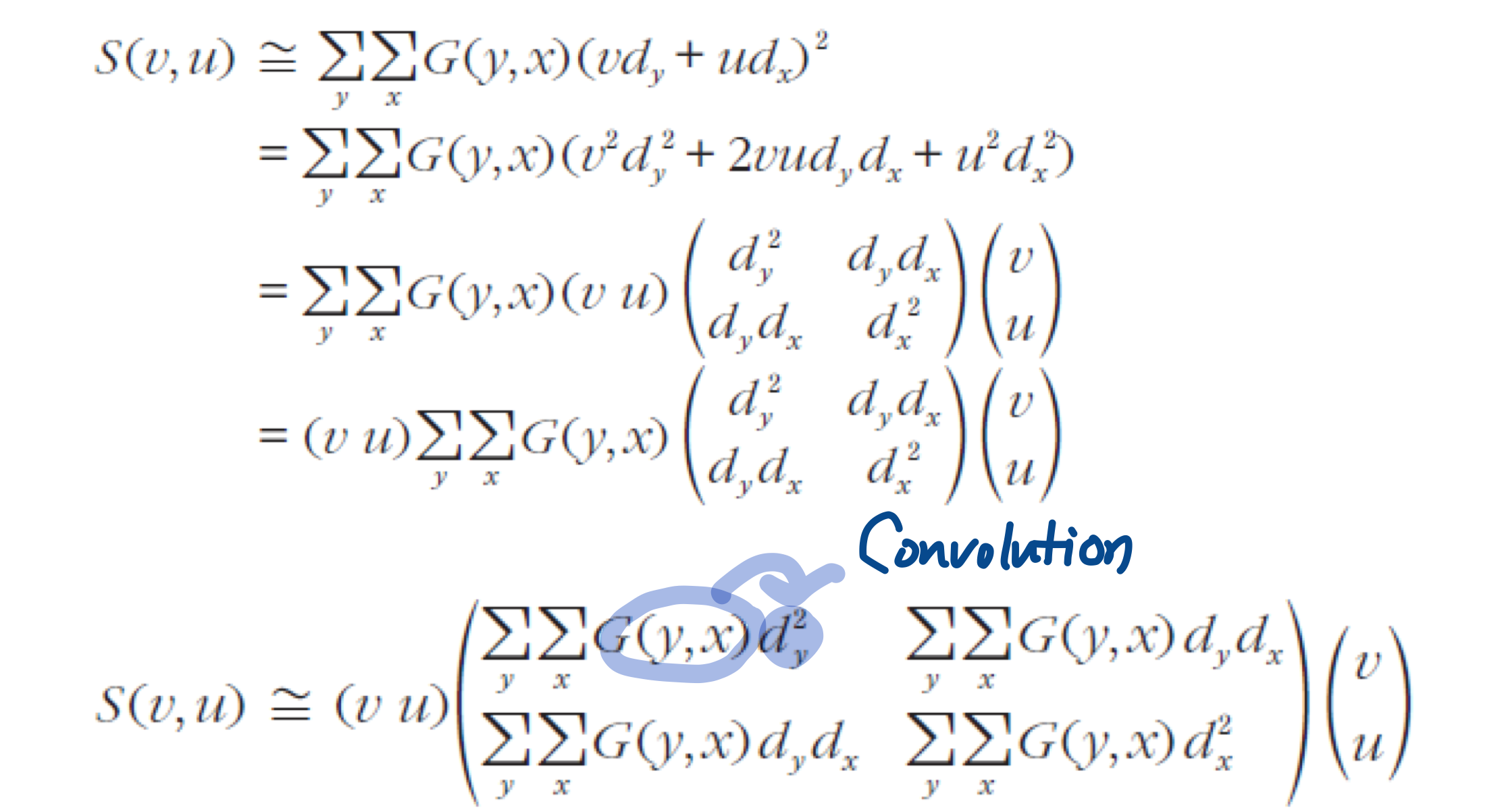
유도식
- $d_y$를 구해서 제곱을 한 후 가우시안 마스크를 컨볼루션한 것
- 2차 모멘트 행렬 A

- (v,u)는 offset으로 실수 가능
- A를 (v,u) 무관하게 계산할 수 있음(S가 u와 A의 곱으로 인수분해되어 있으므로
- A는 영상구조를 나타냄 -> A를 잘 분석하면 특징 여부를 판정할 수 있음
- 예제 : 아래의 12x12 영상 f에서 행렬 A를 계산해보자. 가우시안 마스크는 $\sigma = 1.0$인 G를 사용

영상 f와 가우시안 마스크 G - $d_y, d_x$를 구하기 위해서 각각 $[-1 0 1]^T$, [-1 0 1] 연산자 사용

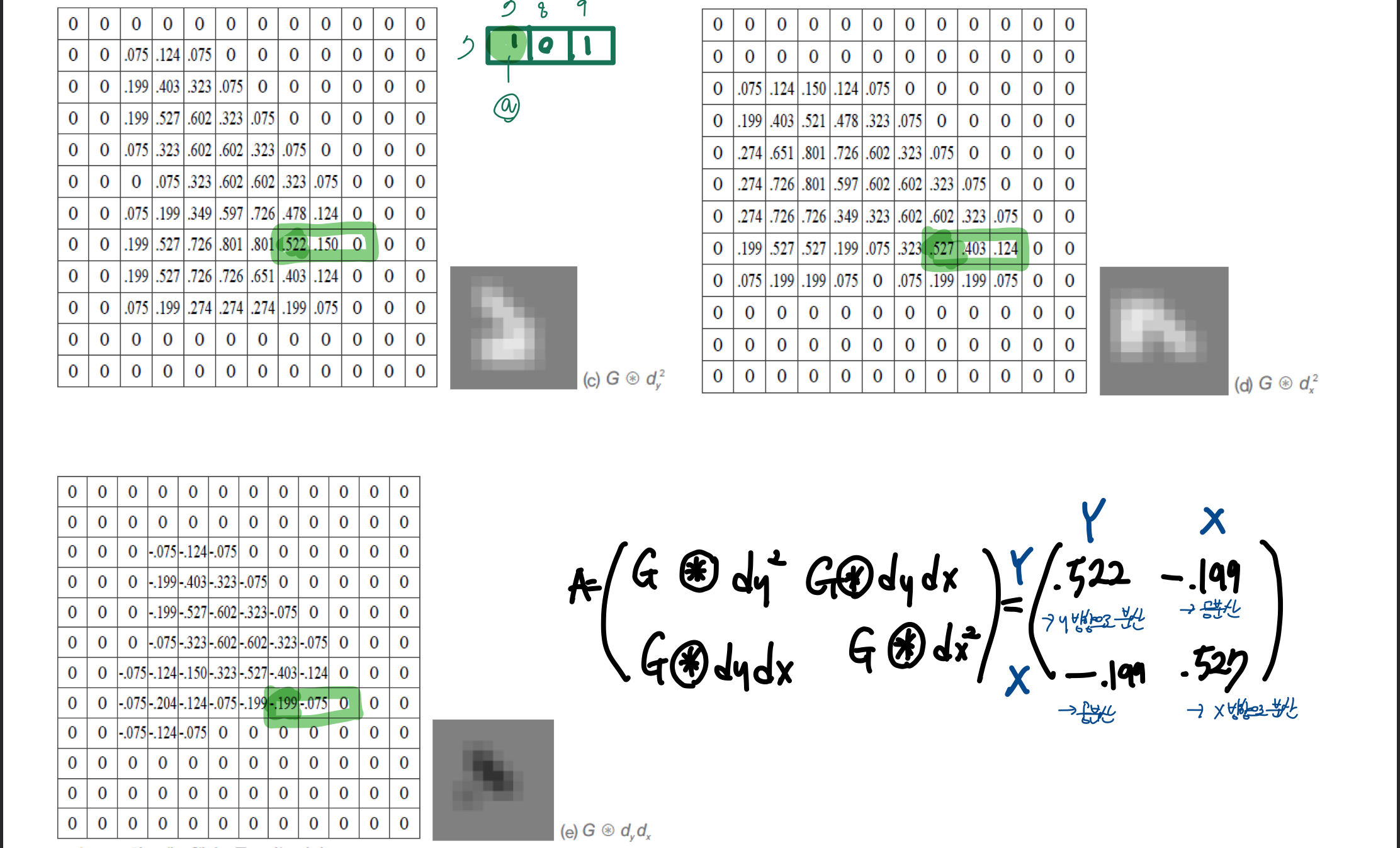
2차 모멘트 행렬 A를 구하는 과정
- A는 공분산행렬(Covariance Matrix)로 행렬의 대각선 원소는 각 변수의 분산을 포함하며, 대각선 이외의 원서는 가능한 모든 변수 쌍간의 공분산을 포함함
- 2차 모멘트 행렬의 고유값 분석
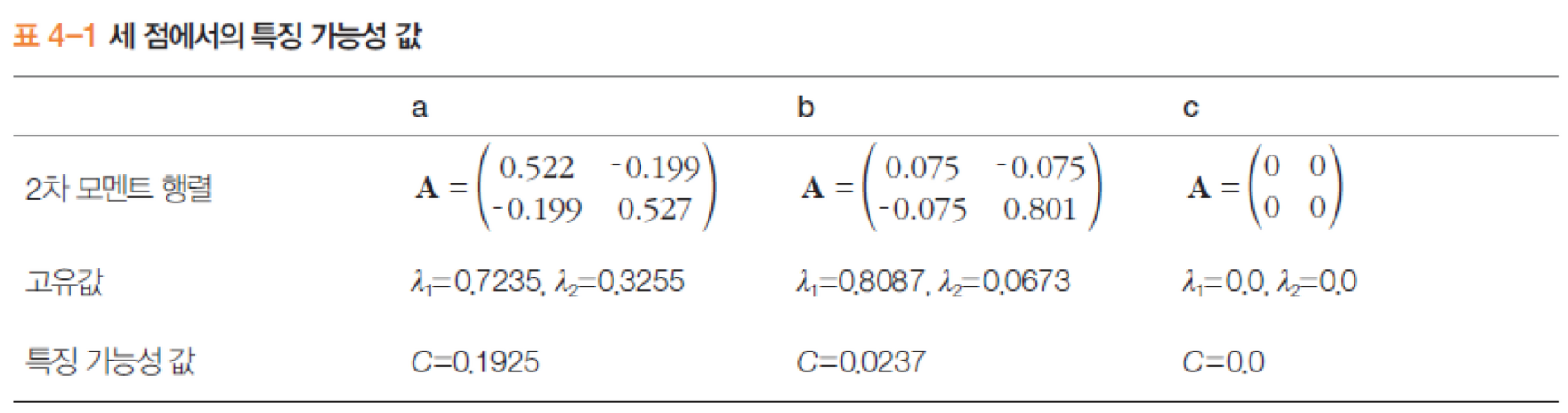
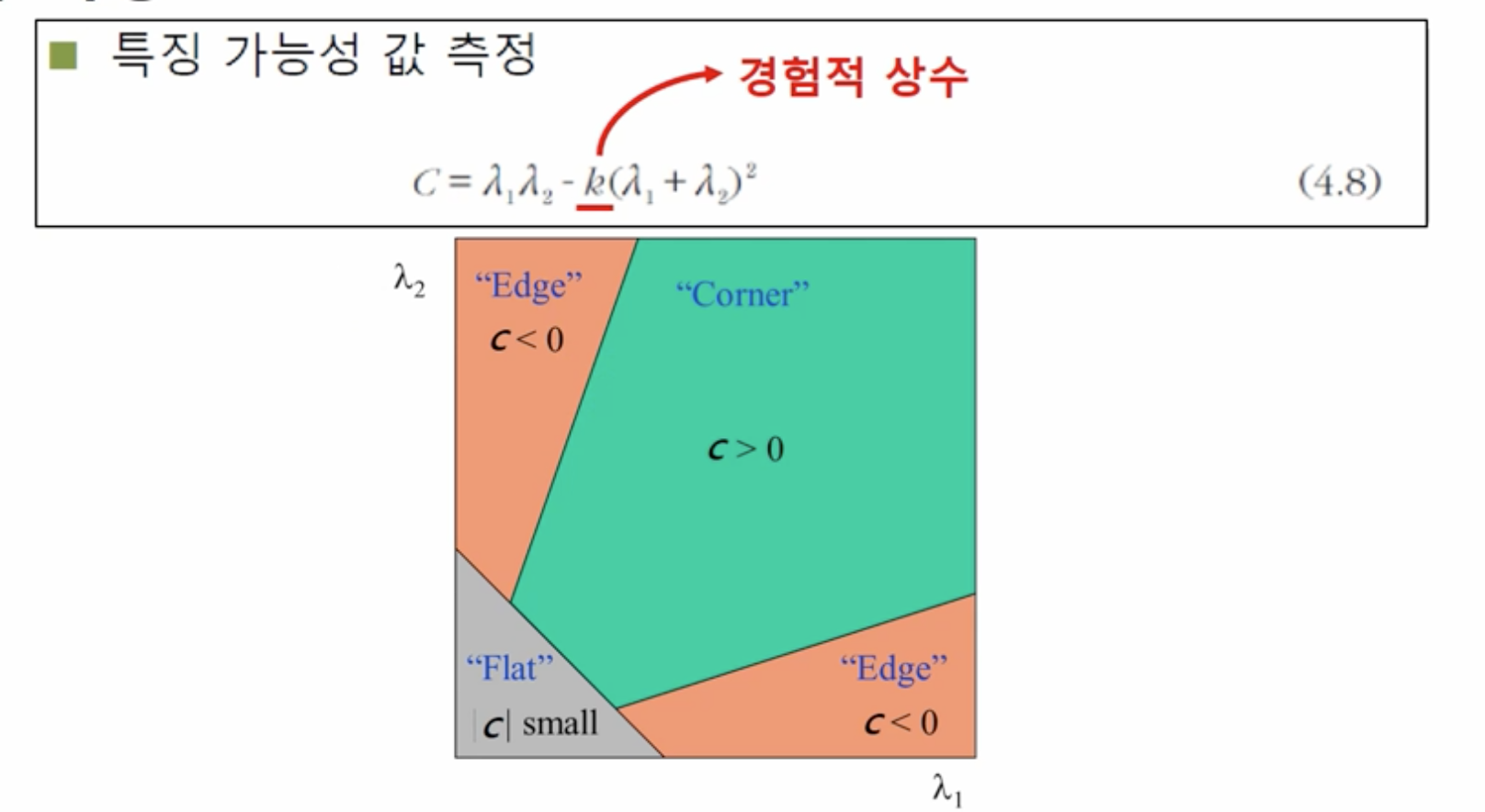
- c와 같이 두 개의 고유값 모두 0이거나 0에 가까우면 -> 변화가 거의 없는 곳(Flat)
- b와 같이 고유값 하나는 크고 다른 하나는 작으면 -> 한 방향으로만 변화가 있는 에지(Edge)
- a와 같이 고유값 두개가 모두 크면 -> 여러 방향으로 변화가 있는 지점. 특징점으로 적합하다(Corner)
- 고유값 계산 방법
- 특징 가능성 값 측정
- $C = \lambda_1 \lambda_2 - k(\lambda_1 + \lambda_2)^2$
- 고유값 계산을 피해 속도 향상
- 위치 찾기 문제 대두

- 큰 C값을 가진 큰 점들이 밀집되어 나타나므로 대표점 선택 필요
- 코너라는 용어가 적절한가?
- 코너 -> 특직정 또는 관심점
2.3 2차 미분을 사용한 방법
- 헤시안 행렬(Hessian Matrix)
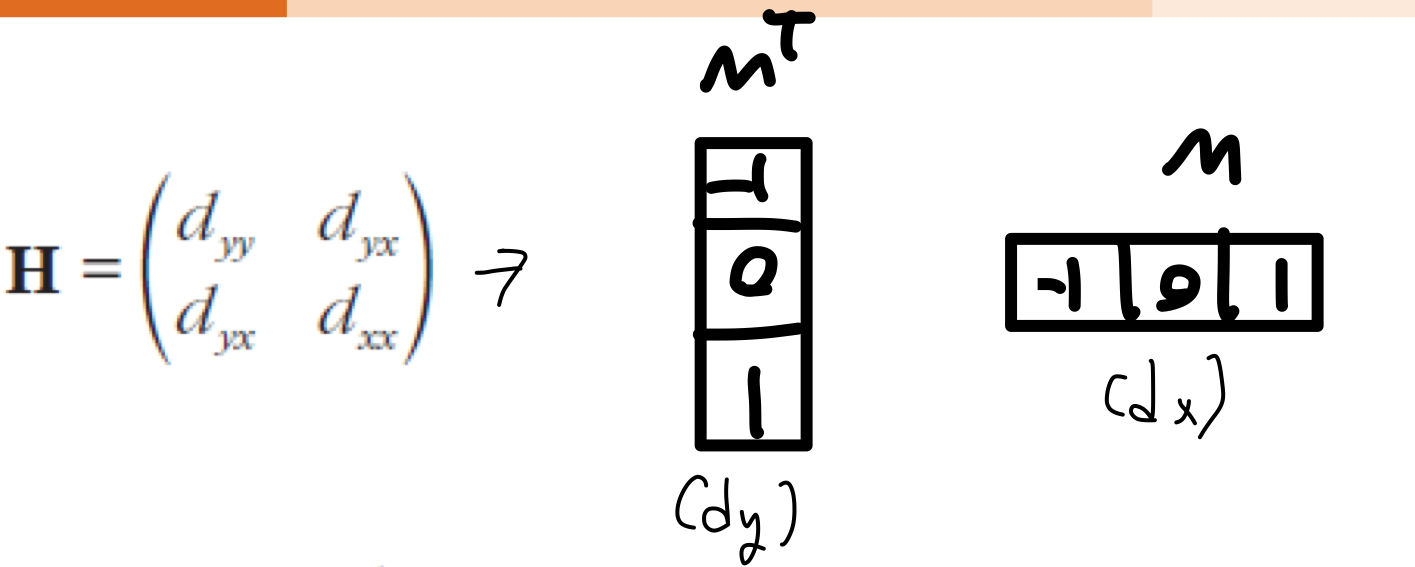
- 가우시안을 포함한 헤시안 행렬
- 2차 미분에서 특징 가능성 값 측정
2.4 슈산
- 원리

- 중심점과 인근 지역의 밝기 값이 얼마나 유사한지에 따라 특징 가능성 결정
- 즉, Center를 기준으로 원형 모형으로 주변에 같은 값을 가지는 픽셀이 몇개인지에 따라 특징점/에지 구분
- 전부 : 특징점X
- 1/2 : edge
- 1/4: 특징점 가치가 높음
3. 위치 찾기 알고리즘
- 앞에서 정리한 여러가지 특징 가능성 측정 방법
- 해리스 적용 예시
- 큰 값이 밀집되어 나타남-> 대표점 선택 필요

- 비최대 억제
- 이웃 화소보다 크지 않으면 억제됨, 즉 지역 최대만(Local Maximum) 특징점으로 검출됨
- 이동과 회전에 불변인가? YES
- 이동이나 회전 변환이 발생하여도 항상 같은 지점에서 관심점이 검출된다

회전한 삼각형에서 관심점 검출
- 스케일에 불변인가? NO
- 스케일이 변하면 같은 지점에서 관신점이 검출되지 않음
- 이유 : 연산자 크기가 고정되어 있지 않으므로. 즉, 스케일 변화에 대처하려면 연산자 크기를 조절하는 기능이 필수적임

스케일에 따른 적절한 연산자 크기
<4. 스케일에 불변한 특징점 검출~> 부터는 다음 게시글에서 계속....
https://codingsmu.tistory.com/116
[패턴인식] 지역 특징 검출(2): 스케일에 불변한 특징점 검출
codingsmu.tistory.com
반응형
'인공지능(AI) > 컴퓨터비전(CV)' 카테고리의 다른 글
| [패턴인식] 영상분할(1): 영상 분할의 원리, 전통적 방법 (0) | 2021.12.16 |
|---|---|
| [패턴인식] 지역 특징 검출(2): 스케일에 불변한 특징점 검출 (0) | 2021.12.15 |
| [패턴인식] 에지 검출(2) : 캐니 에지, 컬러 에지, 선분 검출 (0) | 2021.10.24 |
| [패턴인식] 에지 검출(1) : 에지 검출의 기초, 영교차 이론 (0) | 2021.10.24 |
| [패턴인식] 영상 처리(3) : 다해상도, 모폴로지, 컬러 (0) | 2021.10.24 |
![[패턴인식] 지역 특징 검출(1): 이동/회전 불변 특징점 검출, 위치 찾기 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FboIaNC%2FbtriJtLdFZ1%2FAAAAAAAAAAAAAAAAAAAAAOKTN7Ubp0PavijIdbYF-JwqdkXkJJDfCeNN4c895P-x%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DTPwdt1CiUEUxx6SPGzDOAxS8mCc%253D)