[Combinational Logic Circuit] 멀티플렉서(Multiplexer, MUX)

해당 강의노트는 S. Brown and Z. Vranesic, McGraw-Hill의 [Fundamentals of Digital Logic with VHDL Design, 3rd Edition] 책을 기반으로 작성되었습니다

 Multiplexers

    - Multiplexer Circuit

    - Synthesis of a logic function using MUXs

    - Shannon's Expansion Theorem

 

 Multiplexer Circuit

---

멀티플렉서(Multiplexer, MUX)란?

복수 개의 입력 신호로부터 특정 조건에 의해 입력 신호를 한 개만 선택할 때 사용하는 것

 

디멀티플랙서(Demultiplexer, DeMUX)란?

멀티플렉서와 반대의 목적에 사용 됨

MUX, DEMUX

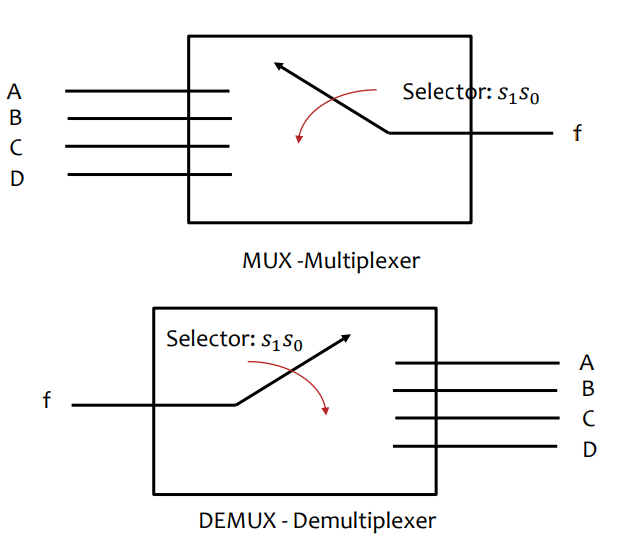
멀티플랙서 회로

- <# of input>-to-<# of output> Multiplexer로 표현

2-to-1 MUX/ 4-to-1 MUX

 

- 같은 Truth table에 대해서 SOP(sum of product)가 아닌 Multiplexer로 구현할 경우 더 간단하게 회로 구현 가능

예시1. SOP회로 -> 2-to-1 Multiplexer 회로 구현

SOP circuit to 2-to-1 Multiplexer

예시2. SOP회로 -> 2-to-1 Multiplexer 2개로 구현

using 2-to-1 MUX to build a 4-to-1 MUX

 

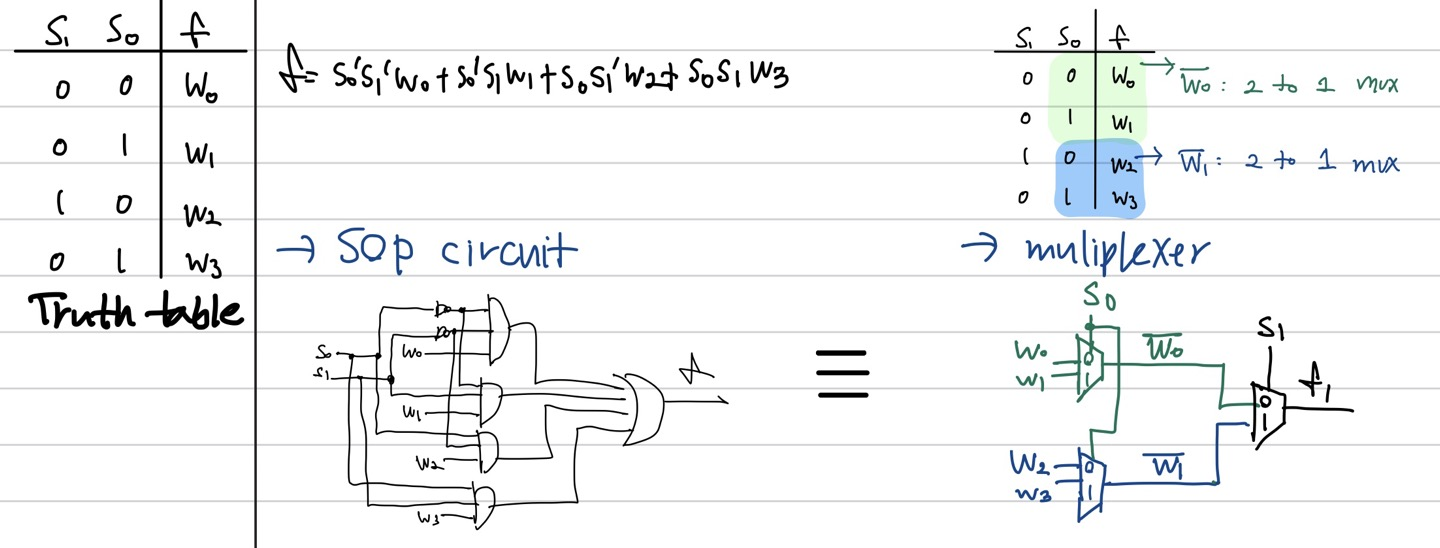
 Synthesis of a logic function using MUX

---

기존의 SOP(Sum of Product) 방식으로 구현한 회로

Sum-of-products implementation

MUX로 구현한 회로

1. input이 두 개인 경우: w1, w2

1. f를 input으로 설정 -> 4-to-1 MUX로 구현 가능

Implementation using a 4-to-1 multiplex

2. w1을 selector로 설정 -> 2-to-1 MUX로 구현 가능

- 4-to-1 MUX 구현보다 더 간단한 형태임

Implementation using a 2-to-1 multiplexer

2. input이 세 개인 경우: w1, w2, w3

예시1. 전가산기(Full Adder)의 Carry값에 대한 Truth table

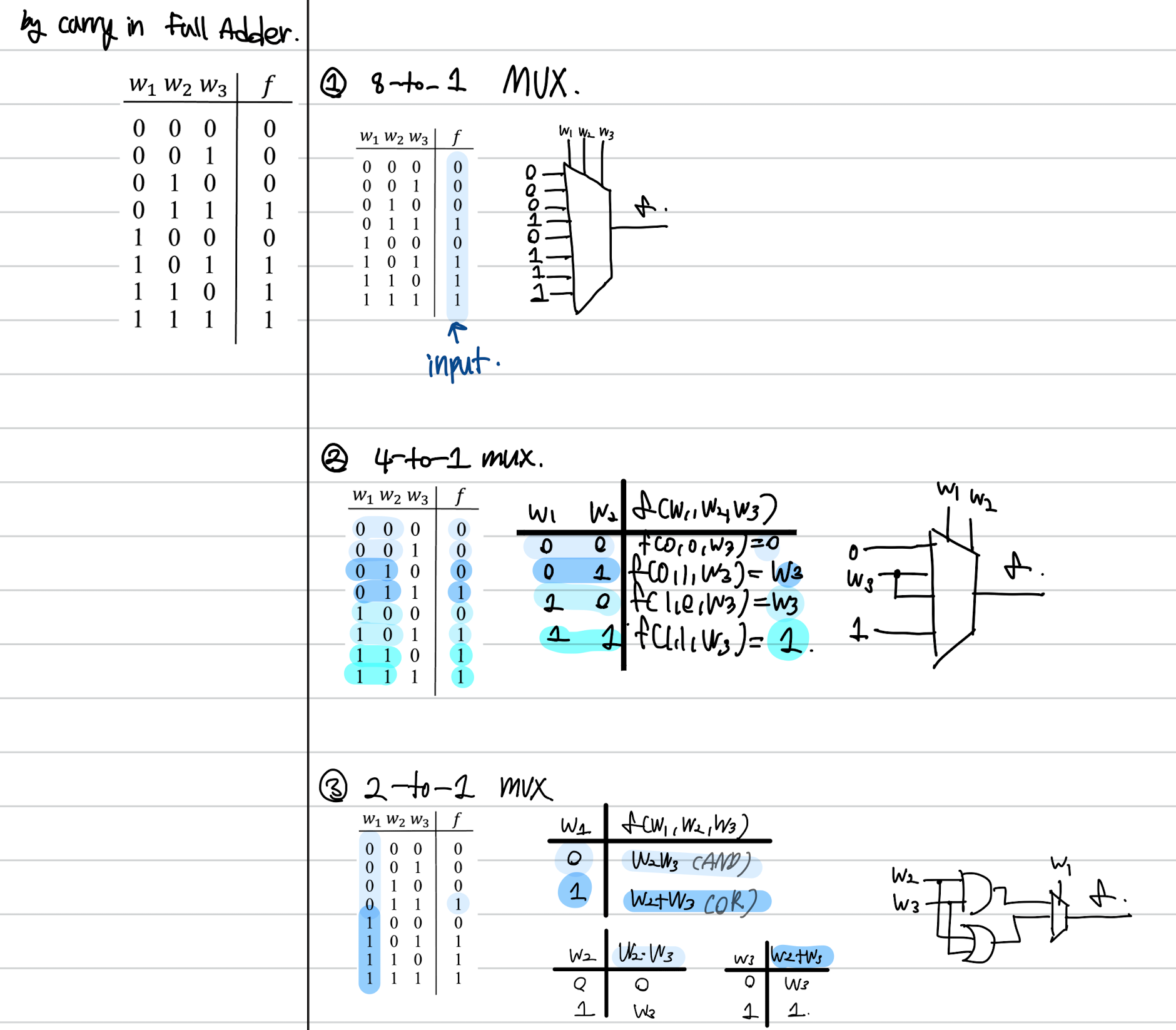
예시2. 전가산기(Full Adder)의 SUM값에 대한 Truth table(= XOR function)

 

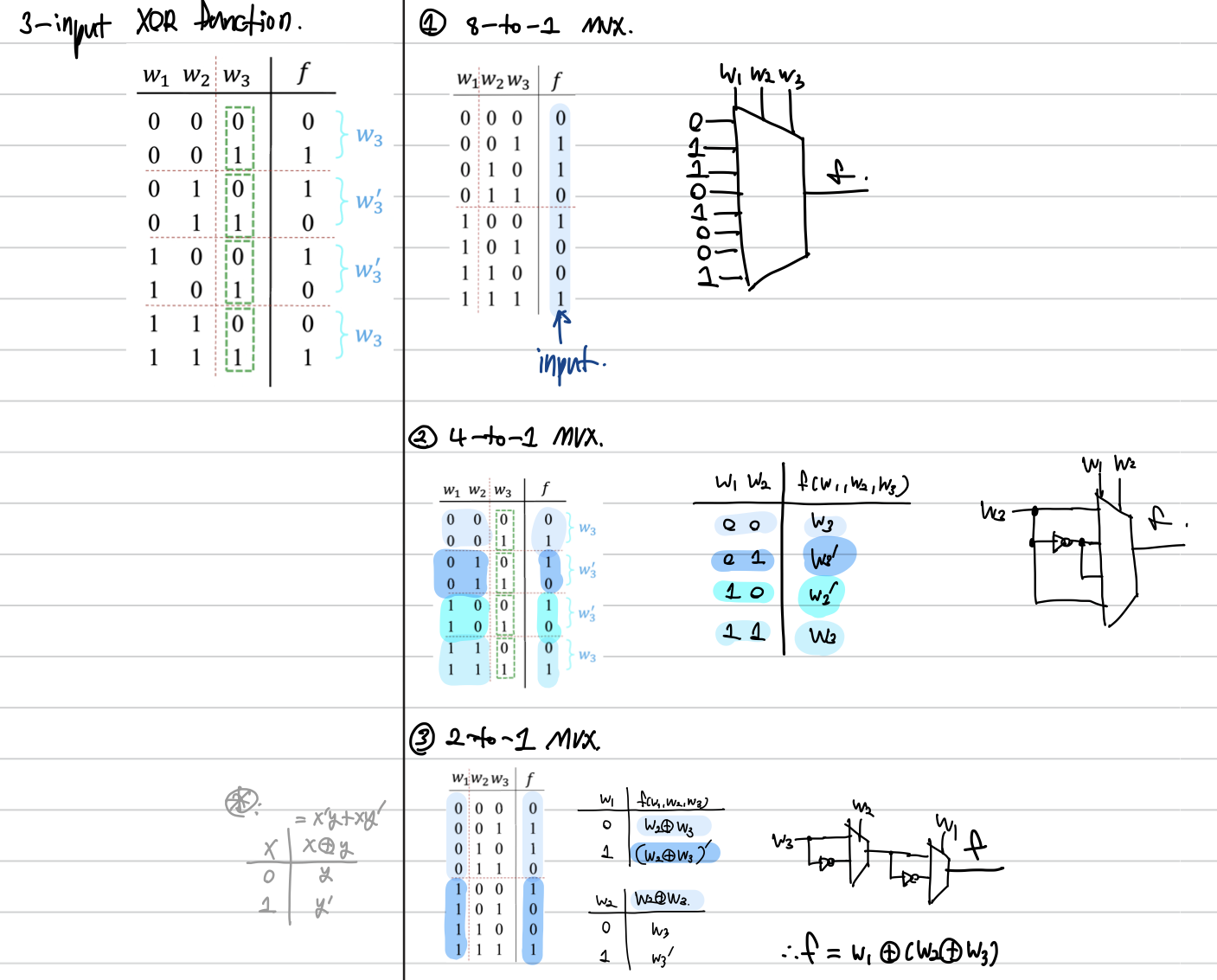
Shannon's Expansion Theorem

---

섀넌의 확장 이론(Shannon's Expansion Theorem)이란?

부울 변수(boolean variable, X)의 관점에서 부울 논리(boolean logic function, F)를 확장하는데 사용되는 이론

$$f(w_1, w_2, \cdots, w_n) = w_1'f(0, w_2, \cdots, w_n) + w_1f(0, w_2, \cdots, w_n)$$

- 기존의 복잡한 회로를 MUX로 간단하게 구현하기 위해서는 selection bit를 잘 골라야 함

- 특정 변수를 selection bit로 뽑하내기 위한 확장이론이 바로 Shannon's Expansion Theorem임

 

예시. 전가산기(Full Adder)의 Carry값에 대한 Truth table(*n=3)

1. w1을 selection bit로 사용: 2-to-1 MUX로 구현

- w1에 대한 f의 cofactor: $f(1, w_2, \cdots, w_n) = f_{w1}$

- w1'에 대한 f의 cofactor: $f(0, w_2, \cdots, w_n) = f_{w1'}$

using 2-to-1 MUX in FA by Shannon's Expansion Theorem

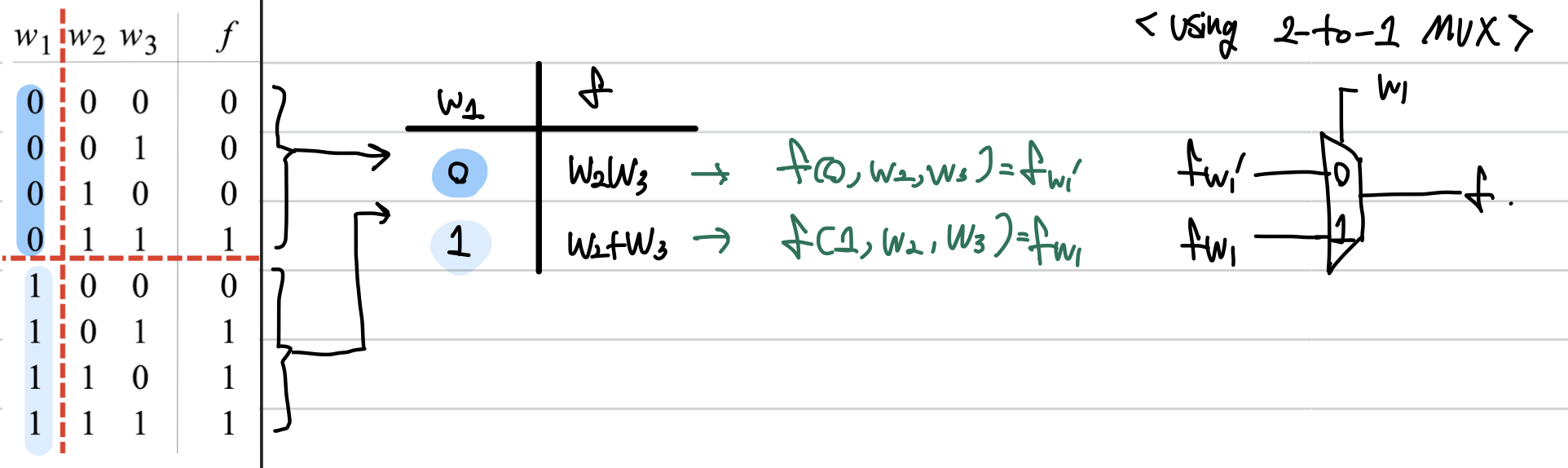
2. w1, w2을 selection bit로 사용: 4-to-1 MUX로 구현

- w1, w2에 대한 f의 cofactor: $f(1, 1, w_3, \cdots, w_n) = f_{w1w2}$

- ...

- w1', w2'에 대한 f의 cofactor: $f(0, 0, w_3, \cdots, w_n) = f_{w1'w2'}$

using 4-to-1 MUX in FA by Shannon's Expansion Theorem

 

예제1. Three input majority function

1-1. $f(w_1, w_2, w_3) = w_1'w_3' + w_1w_2 + w_1w_3$

1-2. $f(w_1, w_2, w_3) = w_1w_2 + w_1w_3 + w_2w_3$

 

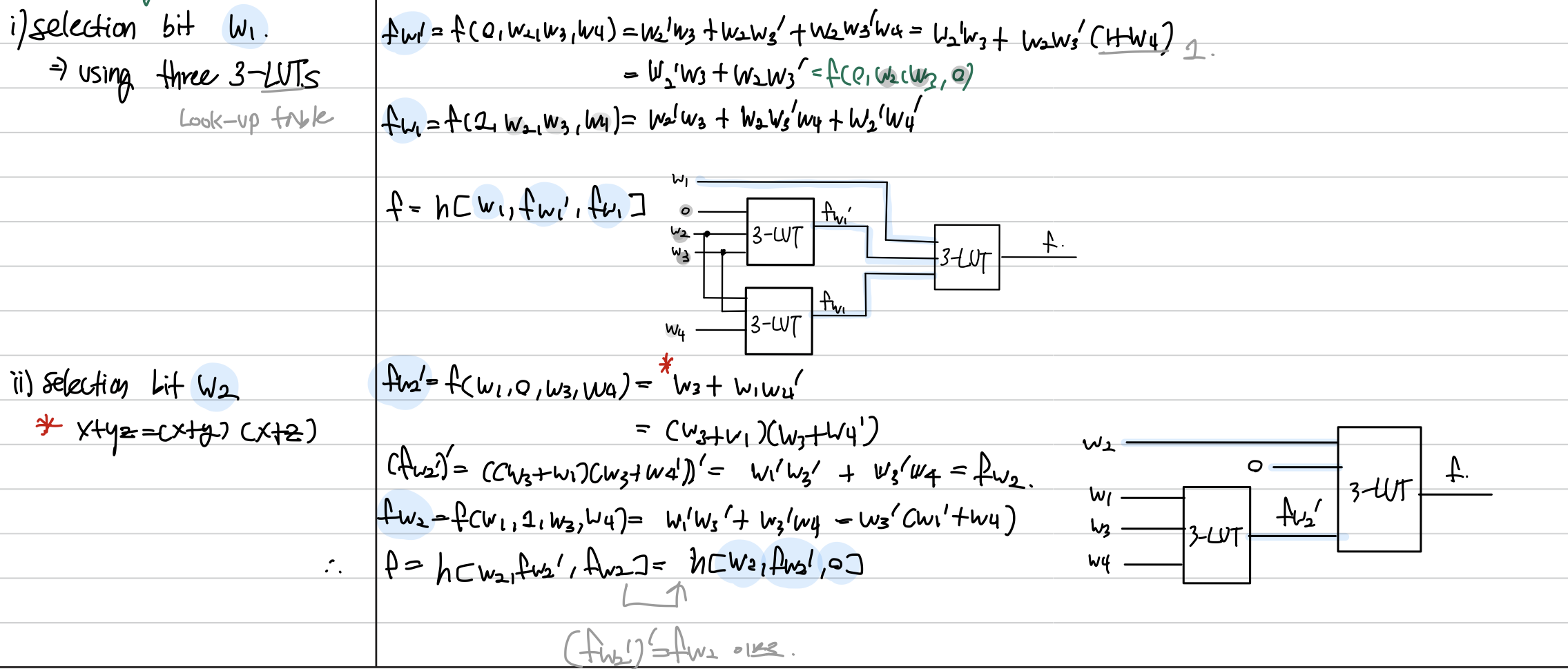
예제2. four input majority function

2-1. $f(w_1, w_2, w_3, w_4) = w_2'w_3 + w_1'w_2w_3' + w_2w_3'w_4 + w_1w_2'w_4'$

- w1보다 w2를 골랐을 때 더 간단하게 회로 구현 가능