반응형
이전 게시글인 <네트워크 플로우(Network Flow)>에 이어지는 알고리즘 개념 글입니다
https://codingsmu.tistory.com/109
이분 매칭(Bipartite Matching)이란?
네트워크 플로우의 개념중에서 이분 그래프(Bipartite Graph)에서의 최대 유량(maximum flow)을 구하는 경우로, 에지의 용량(capacity)이 전부 1인 이분 그래프에서의 최대유량(maximum flow)을 구하는 문제는 이분 그래프에서의 최대 매칭(maximium matching)과 동치이다. 이때 매칭은, 서로 다른 그룹에 놓인 두 정점을 짝지어주는 의미로 이분그래프에서 최대 매칭을 최대 유량 알고리즘인 디닉 혹은 에드몬드 카프 알고리즘을 이용해 구해줄 수 있으나, DFS를 이용하여 O(V*E)시간에 쉽게 구현할 수 있다
이분 그래프(Bipartite Graph)란?

파란색 정점과 빨간색 정점을 각 좌측, 우측으로 재배열한 그래프를 보면, 두 정점들끼리는 어떠한 에지도 존재하지 않다. 이렇게 정점을 두 그룹으로 나누었을 때, 모든 간선에 연결 된 두 정점이 서로 다른 그룹에 존재하는 그래프를 이분 그래프라고 한다
이분 매칭 알고리즘 : DFS(O(V*E))
- 노드1에서 DFS
- DFS 결과, A와 매칭
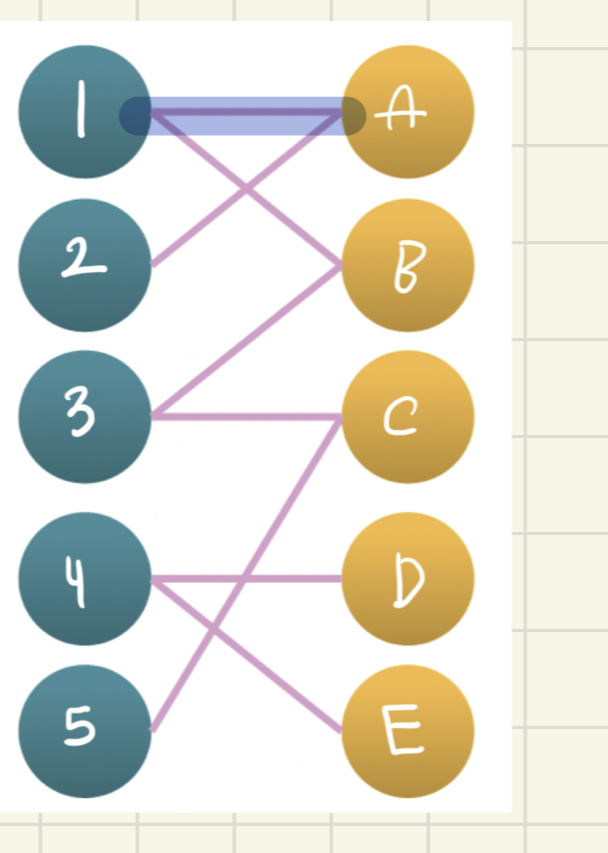
- 노드2에서 DFS
- 노드2에서는 A 방문 -> 이미 <노드1-A>이 매칭된 상황
- 노드1이 B로 갈 수 있으므로 노드1이 양보
- 노드2와 A 매칭, 노드1이 B와 매칭
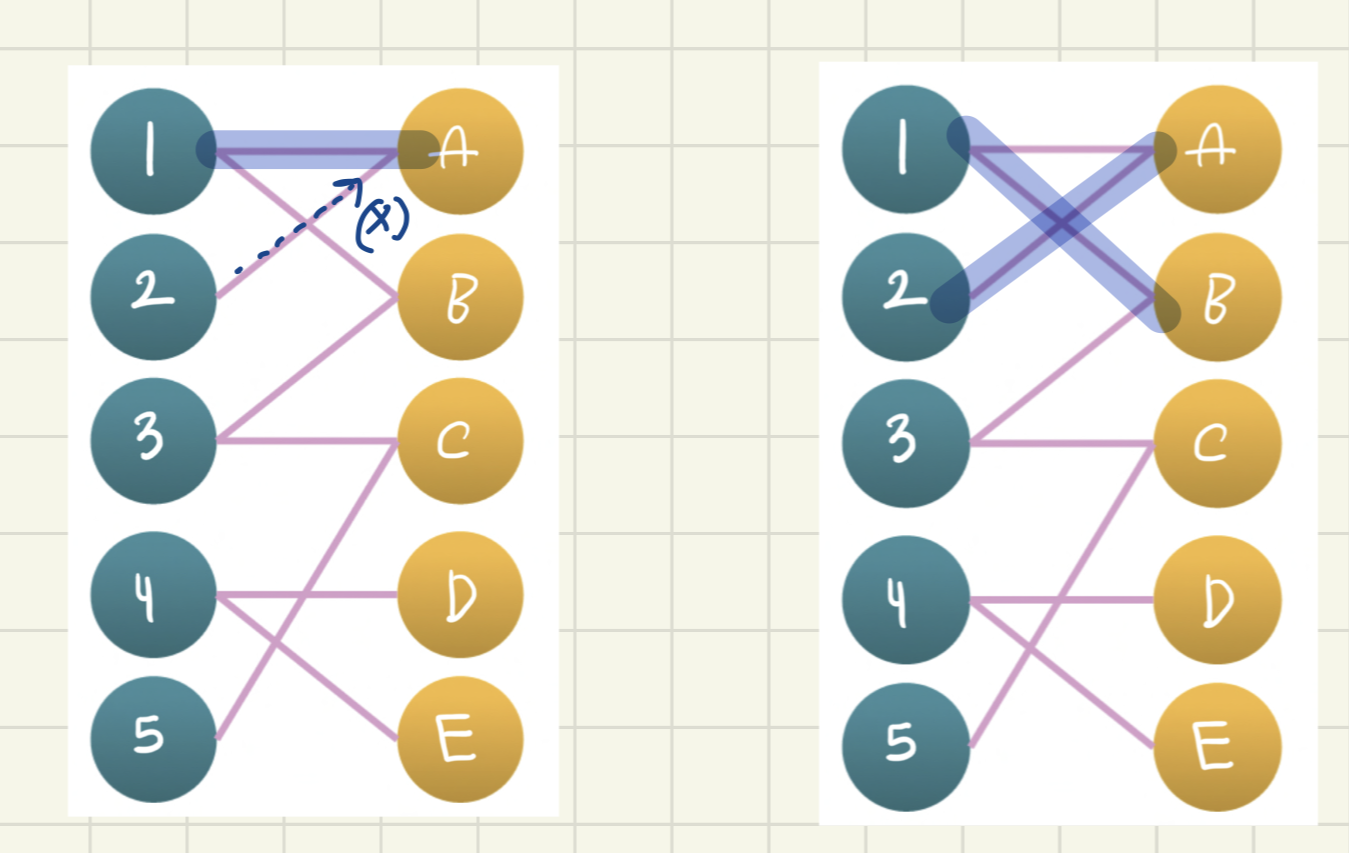
- 노드3에서 DFS
- 노드3에서 B 방문 -> 이미 <노드1-B>이 매칭된 상황
- 노드1이 더 갈 노드가 없으므로 양보 불가
- 노드3에서 C 방문 -> 노드3과 C 매칭

- 노드4에서 DFS
- 노드4에서 D 방문 -> 노드4과 D 매칭

- 노드 5에서 DFS
- 노드5에서 C 방문 -> 이미 <노드3-C>가 매칭된 상황
- 노드3이 더 갈 노드가 없으므로 양보 불가능
- 이분매칭 종료 -> 최대매칭은 4임

구현 코드(C++)
#include <iostream>
#include <vector>
#include <memory.h>
using namespace std;
int N, M;
int match[MAX];
bool visited[MAX];
vector<vector<int>> v(MAX);
bool dfs(int cur);
int main(void){
int ans = 0;
cin >> N >> M;
// intialize bipartite graph
for(int i = 1; i <= N; i++){
int j;
cin >> j;
for(int k = 1; k <= j; k++){
int tmp;
cin >> tmp;
v[i].push_back(tmp);
}
}
// answer is the number of maximum matchings
for(int i = 1; i <= N; i++){
memset(visited, 0, sizeof(visited));
if (dfs(i))
ans++;
}
cout << ans << '\n';
return 0;
}
bool dfs(int cur){
visited[cur] = true;
for(auto there:v[cur]){
int work = match[there];
if (!work || (!visited[work] && dfs(work))){
match[there] = cur;
return 1;
}
}
return 0;
}
반응형
'Algorithm > 알고리즘 이론' 카테고리의 다른 글
| [그래프 이론] 플로이드-워셜(Floyd-Warshall) 알고리즘 (0) | 2022.01.02 |
|---|---|
| 네트워크 플로우(Network Flow) (2) | 2021.11.03 |
| 최소 공통 조상(Lowest Common Ancestor) (0) | 2021.10.04 |
| 단절점(Articulation Point), 단절선(Articulation Bridge) (0) | 2021.09.30 |
| 강한연결요소 : Strongly Connected Component (0) | 2021.09.05 |
