네트워크 플로우(Network Flow)란?
특정한 지점에서 다른 지점으로 데이터가 얼마나 많이 흐르고 있는가를 측정하는 알고리즘으로 네트워크 데이터 전송, 교통 체증 등 다양한 분야에서 활용되고 있음
최대 유량(Maximum Flow)이란?
최대 유량이란 가중치가 있는 방향그래프(Weighted Directed Graph) G와 시작 노드 S, 도착 노드E 가 주어졌을 때, 각 엣지의 용량(Capacity)를 고려하여 S에서 E로 흘려보낼 수 있는 유량의 최대값을 말하는 것이다. 이 때, G의 각 에지 가중치를 용량(capacity)라고 하며 (u,v)의 용량을 c(u,v)라고 쓴다.
예로, 아래와 같은 그래프 G가 있다고 할 때, A에서 D로 최대한 많은 유량을 보내려고 할 때 가장 합리적인 양은 가장 적은 용량이 6이므로, 6임을 알 수 있다. (6이상의 값을 보낼 경우 B->C에서 정체가 발생할 수 있으므로) 이때 표현 방식은 유량(flow)/용량(capacity)이다
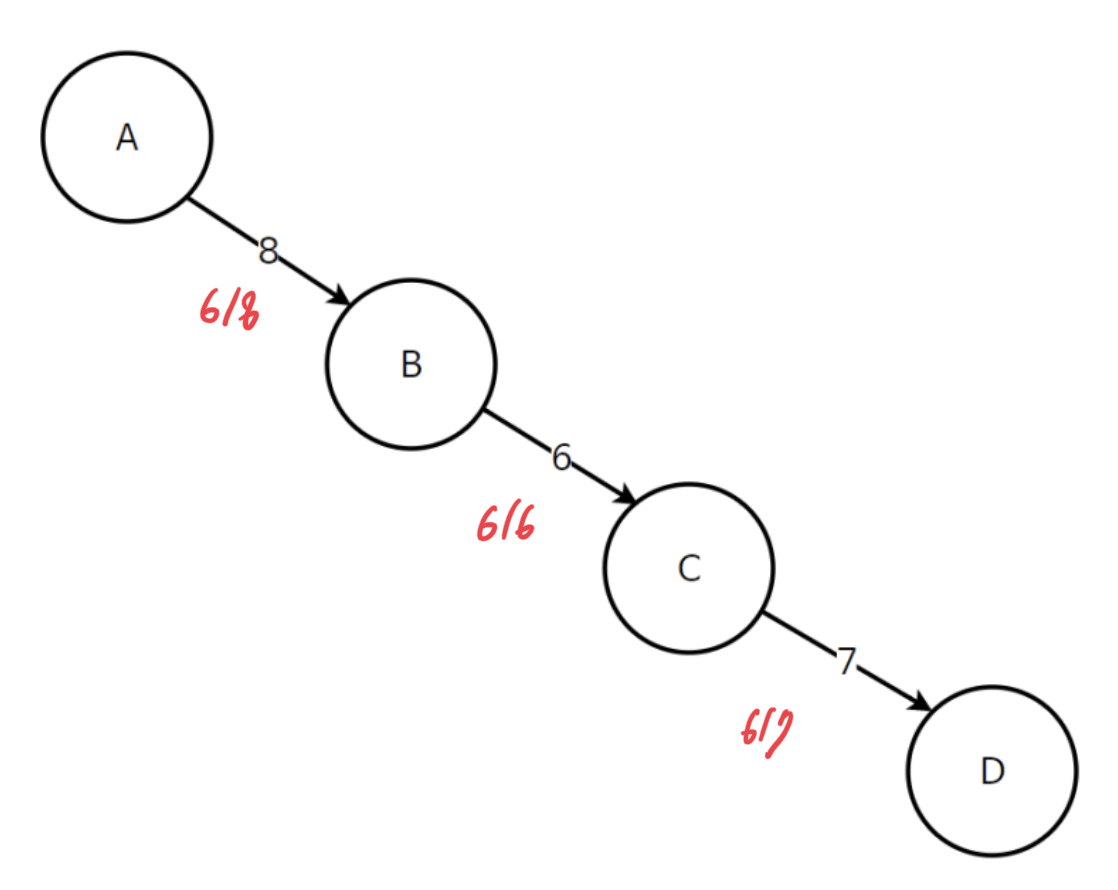
바로 이러한 문제를 해결하는 핵심 알고리즘이 네트워크 플로우 알고리즘이며 이를 최대 유량(Max Flow)문제라고 정의한다
최대유량 문제란?
각 간선에 정해진 용량이 있을 때 A에서 B로 최대로 보낼 수 있는 유량의 크기를 구하는 문제이다. 기본적으로 최대유량문제는 단순하게 가능한 모든 경우의 수를 탐색하는 방법을 사용하며 이때 BFS(너비우선탐색, Breadth First Search)을 이용하는 것이 일반적이다. 이를 에드몬드 카프(Edmonds-Karp)알고리즘이라고도 한다
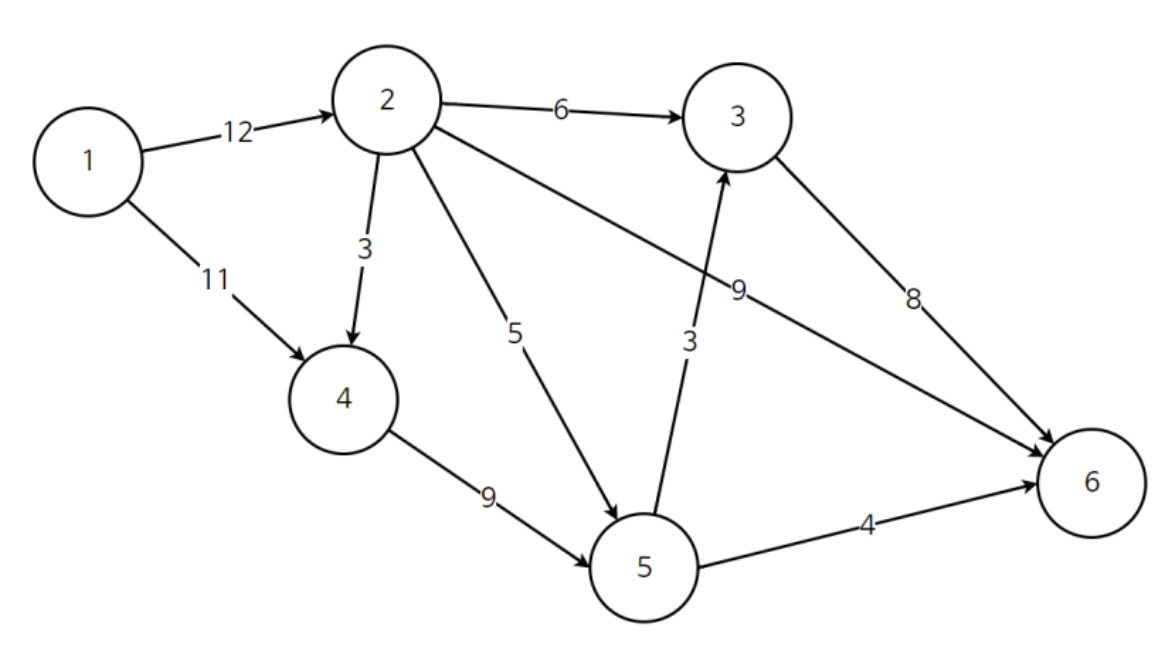
아래의 그래프 G로 1부터 6까지 흘려보낼 수 있는 최대유량은 얼마나 되는지 BFS(또는 Edmonds-Karp)를 사용하여 계산해보자
- 가능한 모든 경우의 수를 탐색하기 위해 유량(Flow)을 모두 0으로 설정
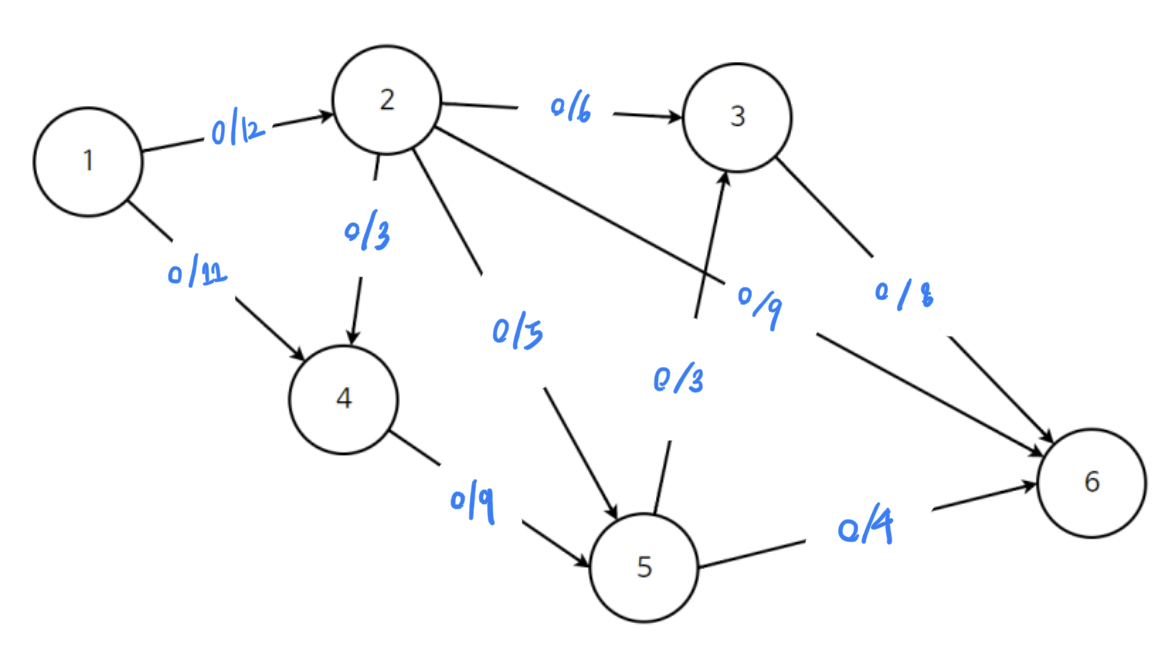
- 정해진 용량(capacity)안에서 가능한 용량양을 반복적으로 더함
- (1->2->3->6) 경우 : 최소 유량 6이므로 6씩 더해줌

- (1->2->6)으로 가는 경우 : 최소 유량이 6이므로 6씩 더해주기. 그 결과, (1->2)로 가는 경로는 12/12로 유량이 꽉참
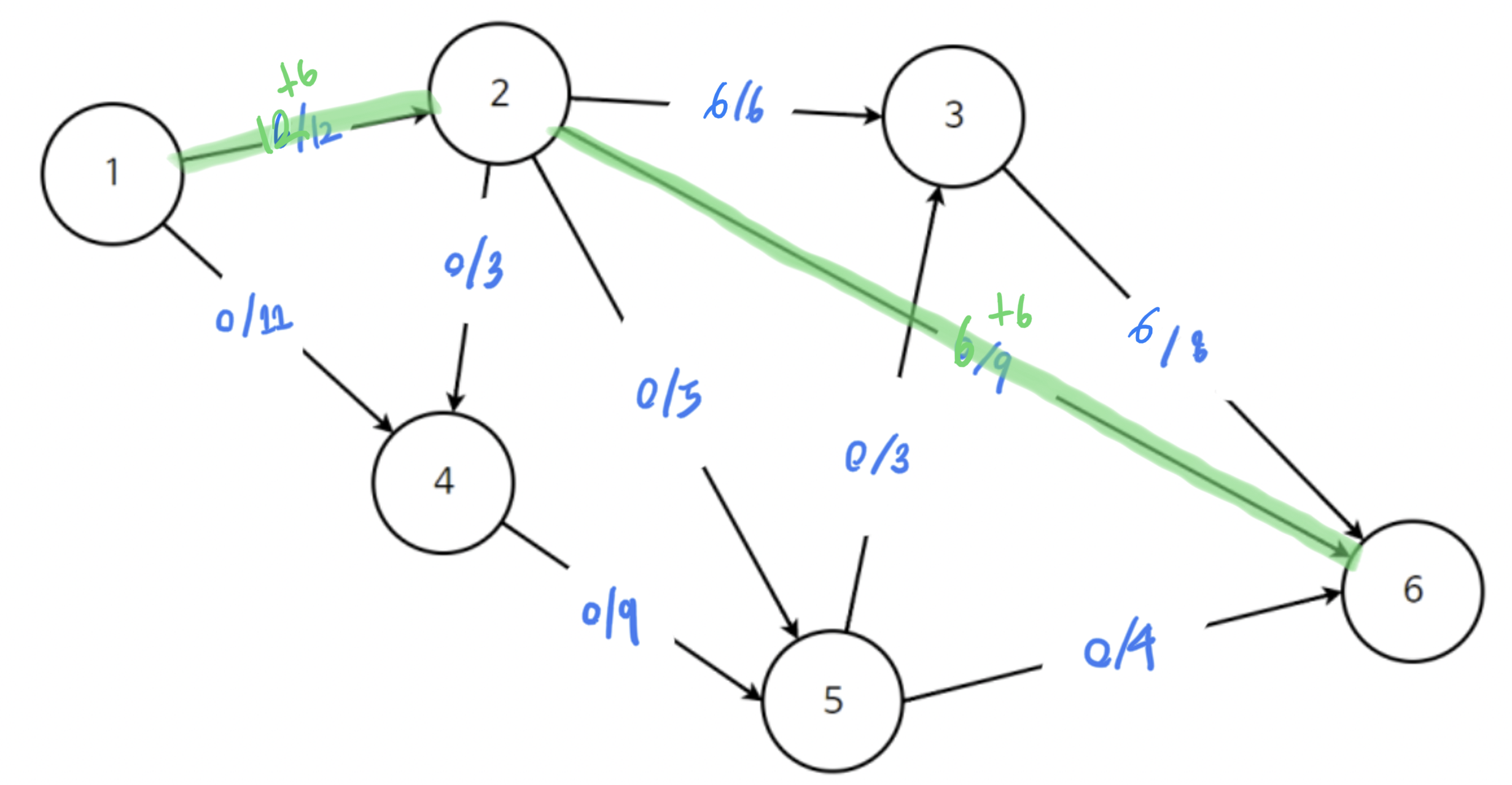
- (1->4->5->6) 경우 : 최소 유량 4이므로 4씩 더해줌

- (1->4->5->3->6) 경우 : 최소 유량이 2이므로 2씩 더해줌
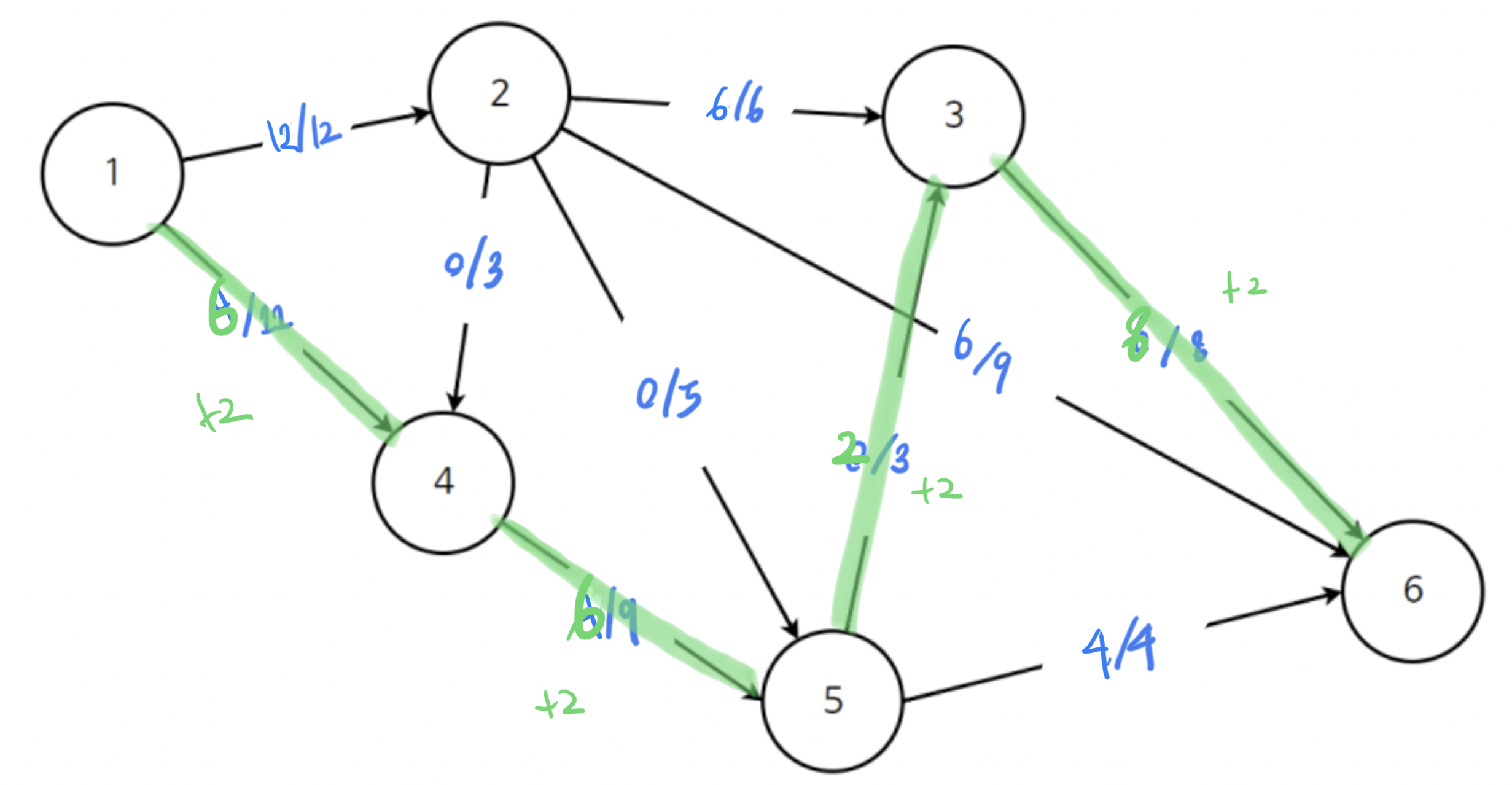
- (1->2->3->6) 경우 : 최소 유량 6이므로 6씩 더해줌
- 음의 유량을 계산 : 모든 가능한 경로를 다 계산해주기 위함으로, 최대 유량 알고리즘의 핵심적인 부분
- (2->3) 경로 : 2에서 3으로 6만큼 흐른다 == 3에서 2로 -6만큼 흐른다
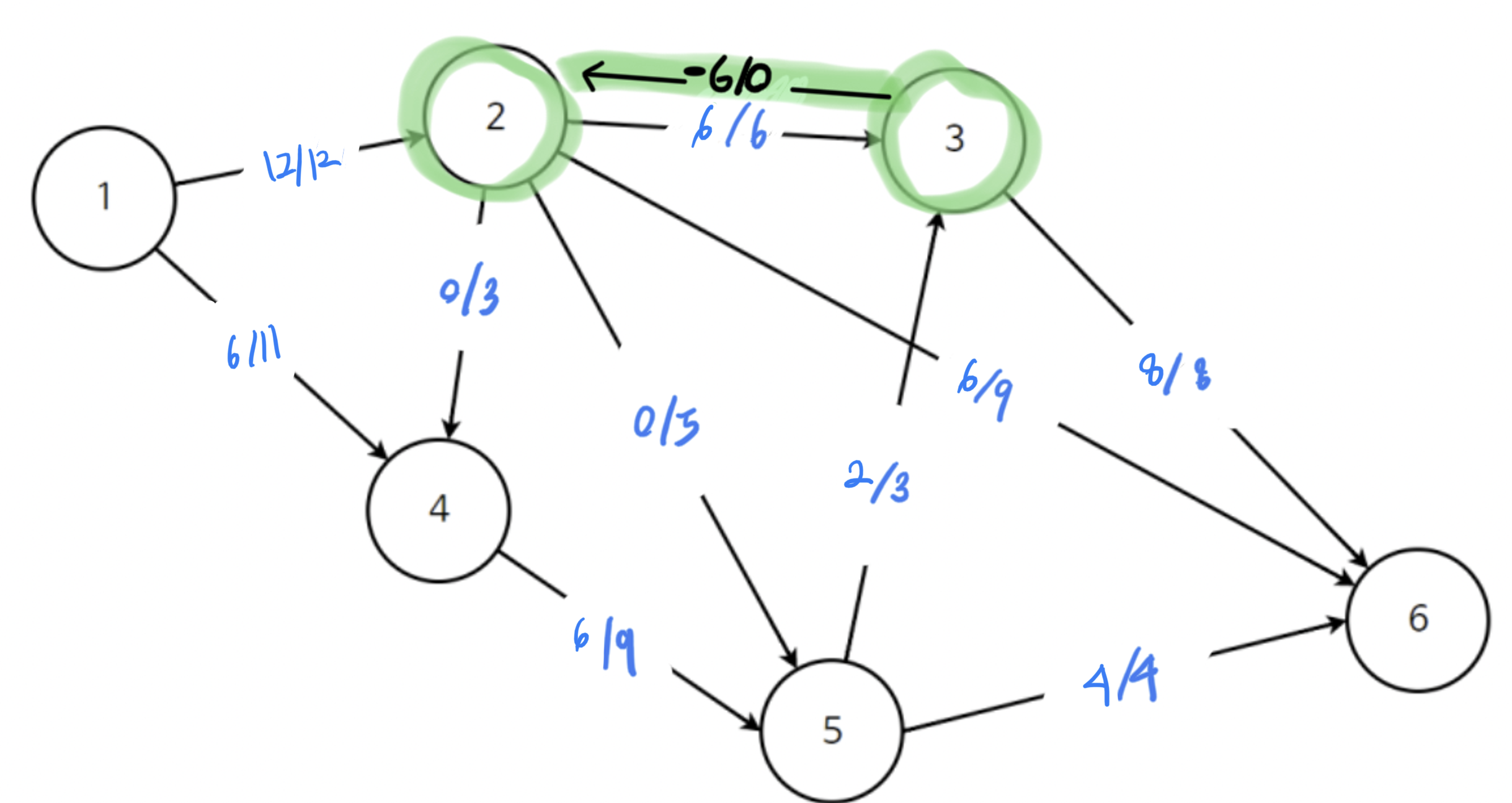
- 이를 모든 경로에 적용하면 아래와 같음

- 위와 같이 음의 유량을 기록하게되면 (1->4->5->3->2->6)과 같이 새로운 경로를 찾을 수 있음

- (2->3) 경로 : 2에서 3으로 6만큼 흐른다 == 3에서 2로 -6만큼 흐른다
- 위에서 구한 (1->4->5->3->2->6)경로가 정점6으로 도달하는 최대유량의 경로가 되며 최대 유량은 19(7+7+7+(-5))이다
위에서는 정리를 위해 순차적으로 설명하였으나, 최대 유량 알고리즘은 사실 순서과 상관없다. 남아있는 양이 1이 넘으면 계속해서 흘려 보내주면 알아서 최적화가 이루어진다는 점에서 특별한 상황이 아니면 유량을 보내는 순서를 고려할 필요가 없다
'Algorithm > 알고리즘 이론' 카테고리의 다른 글
| 이진 탐색(Binary Search)과 매개변수 탐색(Parametric Search) (0) | 2022.03.18 |
|---|---|
| [그래프 이론] 플로이드-워셜(Floyd-Warshall) 알고리즘 (0) | 2022.01.02 |
| 이분 매칭(Bipartite Matching) (0) | 2021.11.02 |
| 최소 공통 조상(Lowest Common Ancestor) (0) | 2021.10.04 |
| 단절점(Articulation Point), 단절선(Articulation Bridge) (0) | 2021.09.30 |
