반응형
단절점(Articulation Point)이란?
하나의 컴포넌트로 구성된 무방향 그래프에서 특정 정점을 제거했을 때 두 개 이상의 컴포넌트로 나눌 수 있는 정점을 단절점이라고 한다
아래의 그래프에서 하이라이트된 정점들이 A-point이다

단절점 구하는 방법
단절점을 구하기 위해서는 먼저 단절점의 특성에 대해 알아야 한다.
어느 한 정점이 단절점이라면, 단절점에 바로 인접해 있는 정점들의 쌍은 단절점이 없으면 우회로로 인해 연결되어 있지 않아야 한다
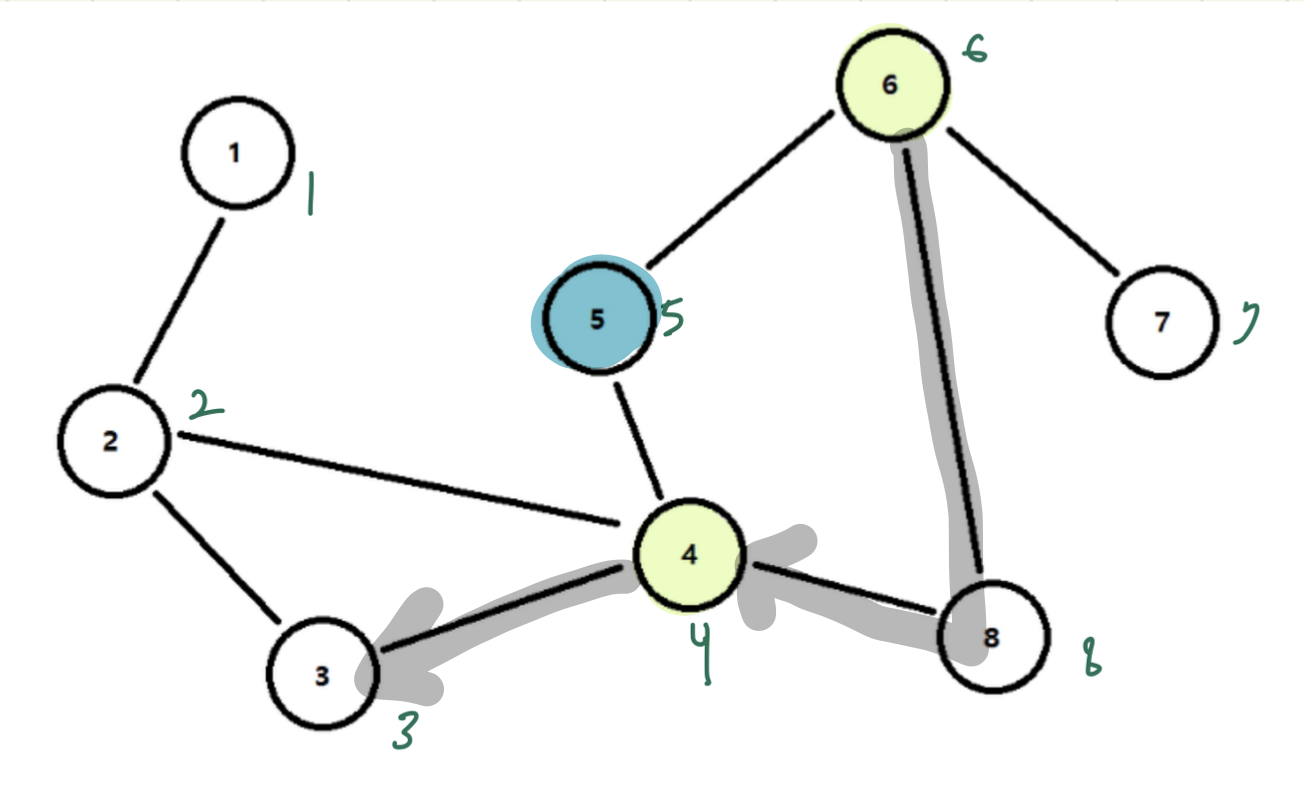
예를 들어 5번 정점이 단절점이라고 생각해보자.
5번 정점을 제거하더라도 인접노드인 4, 6을 우회로(4-8-6)로 연결되어 있으므로 5번은 단절점이 될 수 없다

이번에는 4번 정점이 단절점이라고 생각해보자
4번 정점을 제거하게 되면 (2,3) 과 (5,8)은 우회로를 이용히여 만날 수 있지만 (2,5) (2,8),(3,5),(3,8) 은 만날 수 없다
따라서 4번 정점은 단절점이 된다
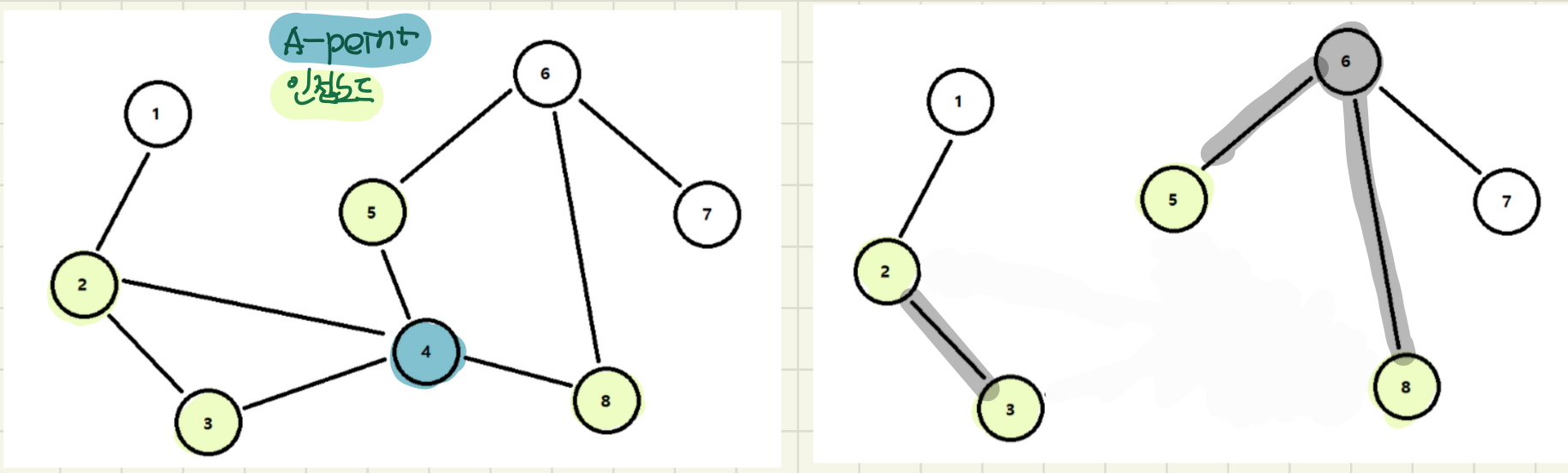
따라서 이 특성을 이용해 아래의 그래프에서 단절점을 구해보자

- DFS를 이용하여 정점들의 방문 순서를 기록
- 특정 정점 u에서 자식 노드들이 정점 u를 거치지 않고 정점 a보다 빠른 방문번호를 가진 정점으로 갈 수 없다면 단절점이다
- u == 5인 경우, 자식노드 6,4가 정점 5를 거치지 않고 방문번호가 더 빠른 노드4(6-8-4), 노드3(4-3)으로 갈 수 있으므로 단절점이 아님
- u == 4인 경우, 자식노드 2,3은 정점 4를 거치지 않고 방문번호가 더 빠른 노드 1(2-1), 노드2(3-2)로 갈 수 있지만, 자식노드 5,8은 불가능하므로 단절점임
- u == 5인 경우, 자식노드 6,4가 정점 5를 거치지 않고 방문번호가 더 빠른 노드4(6-8-4), 노드3(4-3)으로 갈 수 있으므로 단절점이 아님
단, 한가지 예외가 있음
<루트 노드로 잡은 특정 노드의 자식 수가 2개 이상이면 무조건 단절점이다>
해당 방법으로 구하면 단 한번의 DFS로 답을 구할 수 있으므로 O(N+M)의 시간 복잡도를 가지게 된다
반응형
'Algorithm > 알고리즘 이론' 카테고리의 다른 글
| 이분 매칭(Bipartite Matching) (0) | 2021.11.02 |
|---|---|
| 최소 공통 조상(Lowest Common Ancestor) (0) | 2021.10.04 |
| 강한연결요소 : Strongly Connected Component (0) | 2021.09.05 |
| 위상 정렬 Topological Sort (0) | 2021.08.28 |
| [Algorithm : 알고리즘] 06 Dynamic Programming: DP (0) | 2020.08.03 |