반응형
플로이드-워셜(Floyd-Warshall) 알고리즘이란?
- 모든 두 노드 u,v 사이에서 가장 최단 거리를 찾는 알고리즘
- 시간복잡도 $O(n^3)$으로 그래프의 크기가 작을 때만 사용 가능
- 음의 에지(negative edge)가 있어도 계산이 가능한 알고리즘
- 단, 음의 사이클(negative cycle)이 있을 경우 불가능
기본 개념: $A^k$[i][j]
- 노드 i에서 j까지의 최단거리 비용에는 $index <= k$인 중간 노드(intermidiate node)들만 사용해야 함
- 단, k = -1인 경우 i, j에 연결된 에지의 가중치(weight) 값과 비교
$A^k$[i][j]의 의미는?
- i부터 j까지의 경로 중에 최소 비용(minimum cost)을 계산 시, 최단거리가 k보다 큰 노드를 지나쳐서 가는 경우를 제외
-
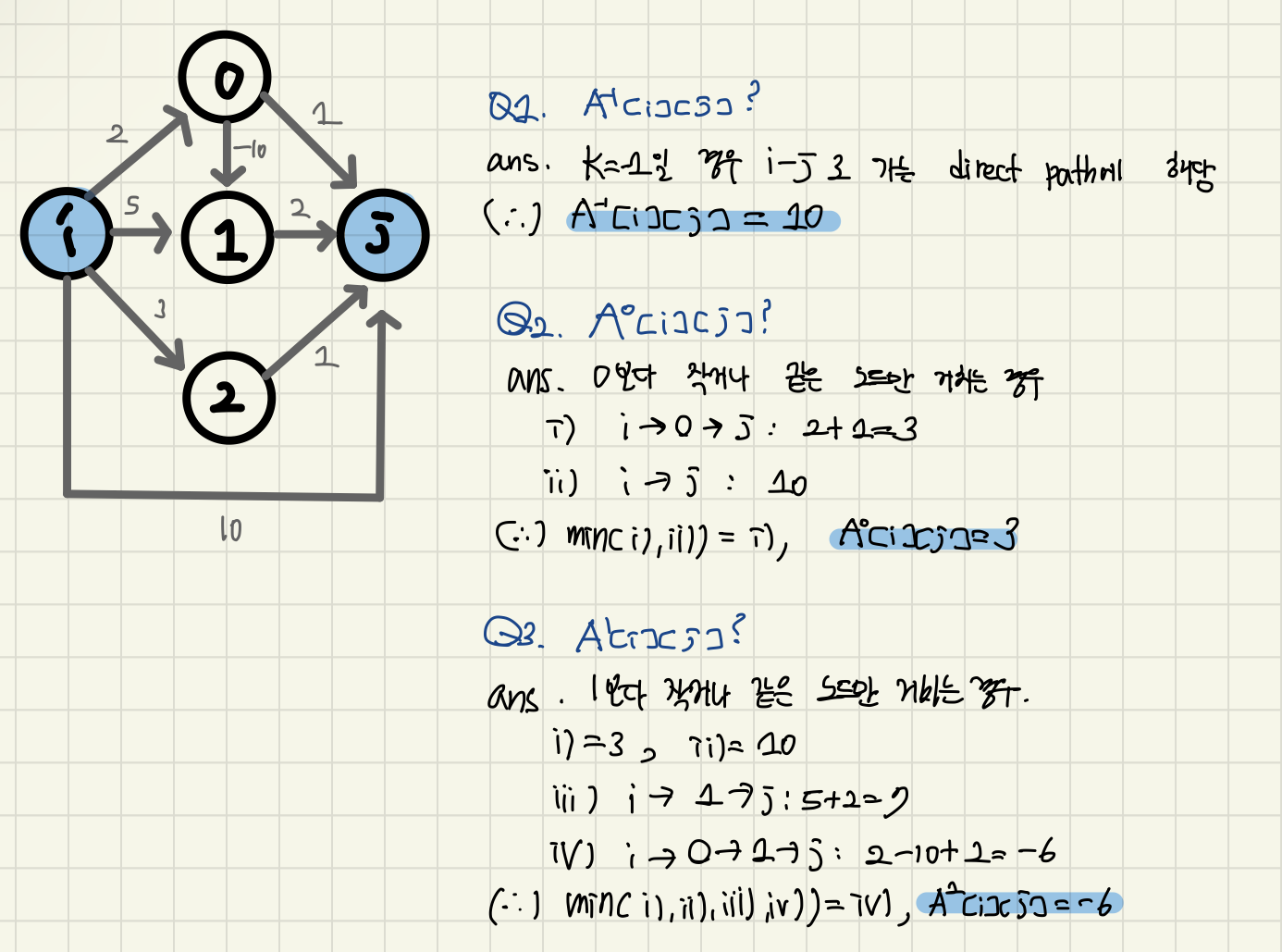
$A^k$[i][j]의 계산은?
$A^k$[i][j] = min($A^{k-1}$[i][j], $A^{k-1}$[i][k] +$A^{k-1}$[k][j])
- k를 지나는 경우:$A^{k-1}$[i][k] +$A^{k-1}$[k][j]
- k를 지나지 않는 경우:$A^{k-1}$[i][j]
소스코드로 구현(Python)
1) adj 에 저장된 인접 행렬의 값을 활용하여 최단 거리 배열인 dist 배열을 초기화
dist = [[0]*n for _ in range(n)]
for i in range(1, n+1):
for j in range(1, n+1):
if i == j:
continue
elif adj[i][j]:
dist[i][j] = adj[i][j]
else:
dist[i][j] = inf
2) 각 라운드 별로 중간 노드가 될 노드 번호를 for문 가장 바깥의 k로 삼기
내부 이중 for문에는 i,j를 통해 각 노드별 모든 거리를 비교하며, k를 지나는 경우/지나지 않는 경우를 비교해 더 작은 값으로 업데이트
for k in range(1, n+1):
for i in range(1, n+1):
for j in range(1, n+1):
dist[i][j] = min(dist[i][j], dist[i][k]+dist[k][j])
반응형
'Algorithm > 알고리즘 이론' 카테고리의 다른 글
| [문자열] 파이썬으로 구현한 유효한 팰린드롬(Palindrome) (2) | 2023.11.25 |
|---|---|
| 이진 탐색(Binary Search)과 매개변수 탐색(Parametric Search) (0) | 2022.03.18 |
| 네트워크 플로우(Network Flow) (2) | 2021.11.03 |
| 이분 매칭(Bipartite Matching) (0) | 2021.11.02 |
| 최소 공통 조상(Lowest Common Ancestor) (0) | 2021.10.04 |
![[그래프 이론] 플로이드-워셜(Floyd-Warshall) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FcqkTVN%2Fbtrpq7h2m1y%2FAAAAAAAAAAAAAAAAAAAAAM-M2p-0hXOdeJQHw1PxecUdAhRqTZ0Q7G0Nqc8o6Ofo%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DkOpFiJWoB0mByMTQeHF8lK5j9Sg%253D)