반응형
Matching
목차
0. PREVIEW
1. 매칭의 기초
2. 기하 정렬과 변환 추정
3. 웹과 모바일 응용
0. PREVIEW
매칭

- 어떤 대상을 다른 것과 비교하여 같은 것인지 알아내는 과정
- 여러가지 문제를 해결하는 열쇠(물체인식, 자세 추정, 스테레오, 증강 현실 등)
생각해 볼 점
- 거짓 긍정(False Positive)을 어떻게 찾아 배제할 것인가?
- 매칭 속도
- 두 영상의 특징점 개수가 m,n이고 특징 벡터의 차원이 d라면, 두 영상을 매칭하는데 $\theta(mnd)$시간 소요
- 실시간 처리가 가능할까?
1. 매칭의 기초
1.1 거리 척도
유클리디안 거리 vs. 마할라노비스 거리

- 유클리디안 거리(Euclidean Distance)
- 두 점 사이의 거리를 계산할 때 흔히 쓰는 방법으로, 이 거리에 대응하는 노름을 유클리드 노름이라고 부른다

- 마할라노비스 거리(Mahalanobis Distance)
- 공분산 행렬 $\sum$을 이용하여 확률 분포를 고려(c가 더 가까움)
- 공분산 행렬의 역행렬을 곱해주는 이유
- 분산이 큰 방향에 대해서는 역에 해당하는 term을 곱해줌으로써 큰 분산에 대해 정규화(Normalize)하는 역할

- $\mu$와 b, c의 거리를 각각 유클리디안, 마할라노비스 거리로 계산해보자
-
더보기

중심을 구하는데 사용한 데이터들이 가로 길이가 더 기므로 마할라노비스거리로는 c가 b보다 중심 $\mu$에 가깝다

-
화이트닝 변환
- 공분산 행렬이 단위 행렬 I가 되도록 원래 백터 x를 y로 변환
- $\sum = I$이면 두 거리 척도가 같음
- 화이트닝 변환 시, 주어진 점들을 분산이 동일하도록 모두 정규화(Normalize)해준다
- 정규화 이후 거리는 유클리디안으로 계산
- 아래의 공분산 행렬의 고유 벡터와 고유값을 계산해 식(7.4)를 구성해보자
1.2 매칭 전략과 성능 분석
매칭을 활용하는 여러 가지 상황
- 파노라마 영상 제작
- 두 영상이 동등한 입장에서 참여
- 물체 인식 또는 증강 현실
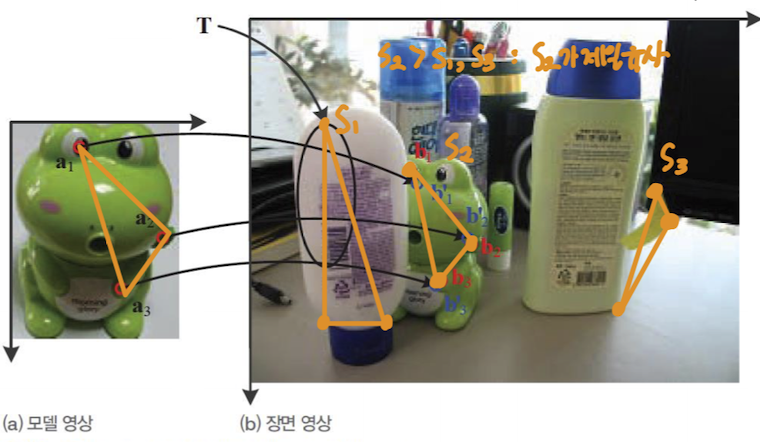
- 모델 영상을 깨끗한 배경 위에 물체가 놓임
- 장면 영상은 심한 혼재와 가림이 발생
단순한 매칭 전략
- 두 영상의 특징 벡터를 $a_i (i=1,2,\cdots,m), b_j (j=1,2,\cdots,n)$라 표기할 때, 아래 식을 만족하면 매칭 성공
- $d(a_i, b_j) < T$
ROC를 이용한 성능 분석

- ROC, Reciever Operating Characteristic Curve
- 임계값 T가 낮으면 거짓부정(FN)이 많아지고, 높으면 거짓긍정(FP)이 많아짐
- T를 점점 키우면서 측정한 거짓 긍정률과 참 긍정률을 나타낸 그래프가 ROC
- 왼쪽 위 구석에 가까울수록 좋은 성능
- AUC(곡선 아래 면적): 성능을 하나의 수치로 표현할 때 사용
- 예제
또 다른 매칭 전략
- 최근접 이웃 전략
- $a_i$의 최근접 이웃 $b_j$가 $d(a_i, b_j) < T$를 만족하면 매칭 성공
- 최근접 거리 비율 전략
- 최근접 $b_j$와 두 번째 최근접 $b_k$가 아래식을 만족하면 매칭 성공
- $\frac{d(a_i, b_j)}{d(a_i, b_k)} < T$
- 실험에 따르면 이 전략이 가장 높은 성능을 보임(예, SIFT [Lowe2004])
2. 기하 정렬과 변환 추정
2.1 최소제곱법과 강인한 추정 기법
REVIEW
- 특징 벡터가 개별적으로 매칭을 수행->이상치(outlier<->inline) 매칭 (거짓긍정) 발생
- 기하 정렬을 이용하여 인라이어 집합을 찾아내고, 변환 행렬을 추정해야 함
여러 상황

- 사람이 개입하여 아웃라이어가 없는 경우: 항공 사진 비교, 의료 영상 정합 등
- 아웃라이어가 있는 경우: 파노라마 영상 제작 등
- 예) [Lowe2004]는 심한 혼재와 가림이 있는 경우 단지 1%만 인라이어인 상황 보고, 즉 99%가 이상치
최소제곱법
- LMS, Least Mean Square
- 오래전부터 수학과 통계 분야에서 사용된 기법
- 예) X집합 중 이를 가장 잘 대표하는 직선을 찾아라 <- 회귀(Regression) 문제
- 직관적으로 $l_1$이 더 좋음

최소 제곱법 - 수학적으로 설명하자면, 점들과 직선과의 거리 평균이 가장 작은, 즉 LMS인 직선의 방정식을 찾아내는 것
- 직선 l까지의 거리의 합을 오차로 공식화

- E(l)을 최소화하는 l을 찾는 것이 목표
매칭 문제로 확장
- 입력은 매칭 쌍 집합 $X=\{(a_1, b_1),(a_2, b_2), \cdots, (a_n, b_n)\}$
- 모델은? -> 변환 행렬

오차 함수 E(T)

최소 제곱법은 아웃라이어가 있으면 오작동
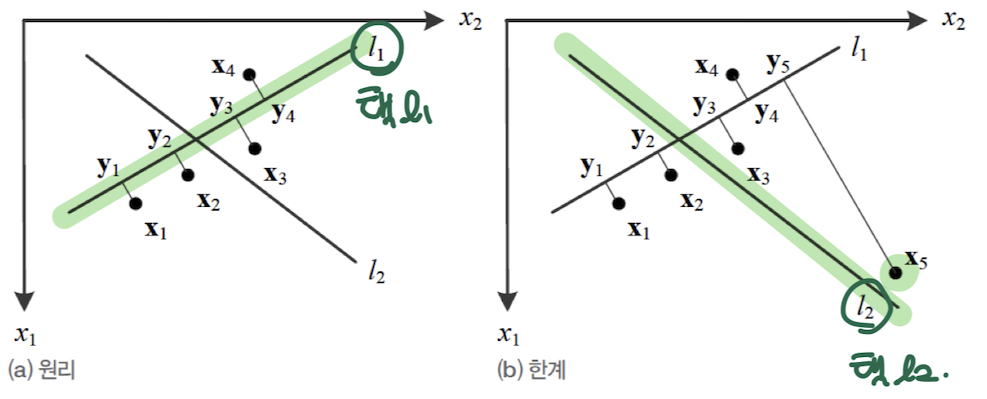
- 예) 아웃라이어 $x_5$가 포함되면 $l_2$를 선호
- 이런 경우에는 강인한 추정 기법이 필요
2.2 RANSAC
원리

직선 검출하는 위의 사진과 같은 원리
해당 장에서는,
매칭 쌍 집합 $X=\{(a_1, b_1),(a_2, b_2), \cdots, (a_n, b_n)\}$을 처리할 수 있게 확장
3. 웹과 모바일 응용
웹과 모바일 환경에서 '인터넷 버전' 연구 분야 태동

- 방대한 영상 발생(예: Flickr에 하루에 올라오는 영상은 350만장)
- 새로운 응용 분야 창출(예: 파노라마, 사진 관광, 증강 현실 등)
- 문제를 푸는 새로운 접근 방법 개발(예: SNS 정보 활용한 얼굴 인식 성능 향상)
3.1 파노라마 영상 제작
제작 사례

스마트폰 앱
- Photosynth
- AutoStitch
제작 과정

3.2 사진 관광
구조 추정 문제

- 같은 장면을 여러 시점에서 찍은 영상들로부터 3차원 정보 복원(Multiview Geometry)
- 장면에 나타난 물체의 자세 정보 복원
- 카메라 시점 정보 복원
- 다양한 응용 문제에 적용 가능
- 예) 사진 관광, 증강 현실 등
- Reconstruction vs. Stereo
- Stereo는 두 가지 영상이 필요하고, 이를 수행하기 위해서는 수평선이 일치해야 함(epipolar geometry)
- Reconstruction은 수평선 일치 뿐만아니라 더 많은 조건이 필요함, 더 어려운 작업임
사진 관광: 3차원 둘러보기
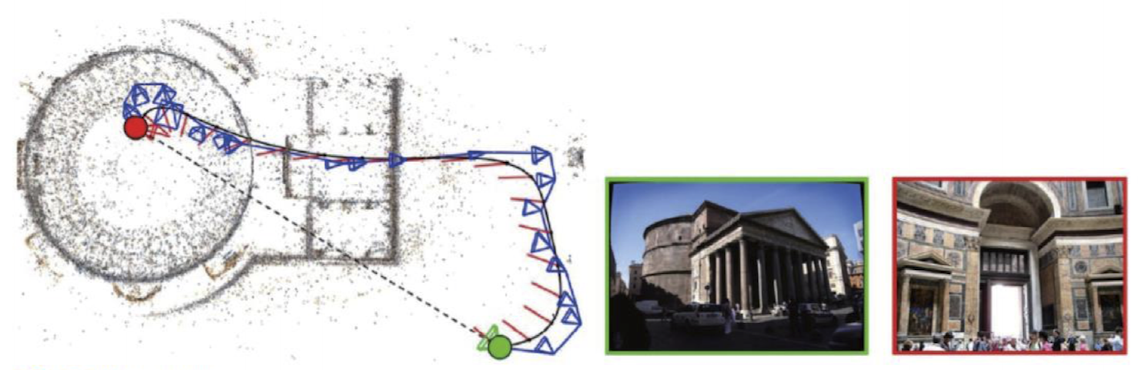
- 파란 삼각형은 복원된 카메라 시점
- 검은 선은 경로 계획 알고리즘으로 계산한 매끄러운 경로
사진 관광: 자동 주석 붙이기

- 모델 영상에 주석을 입력해두면, 새로운 영상에 대해 주석 위치를 자동 추정하여 보여줌
- 일종의 증강 현실에 해당
사진 관광에 필요한 정보를 추정하는 알고리즘
- 시점 변화가 크므로,
- 영상 간의 겹침 관계를 알아내는 과정이 필요
- 겹침 정보를 그래프로 표현
- 그래프의 연결요소를 찾고, 각각에 대해 번들 조정을 수행
반응형
'인공지능(AI) > 컴퓨터비전(CV)' 카테고리의 다른 글
| simCLR을 통해 Contrastive Learning 이해하기 (0) | 2022.12.16 |
|---|---|
| [패턴인식] 특징 기술(2): 특징 기술자, 영역 기술자 (2) | 2021.12.18 |
| [패턴인식] 특징 기술(1): 특징 기술자, 영역 기술자 (0) | 2021.12.17 |
| [패턴인식] 영상분할(2): 민시프트, 대화식 물체 분할 (0) | 2021.12.16 |
| [패턴인식] 영상분할(1): 영상 분할의 원리, 전통적 방법 (0) | 2021.12.16 |
![[패턴인식] 매칭](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbnOUKa%2FbtrogvC32pp%2FAAAAAAAAAAAAAAAAAAAAALnfu5o90gKmUPMHy1CV1AcQgs3L1F_XsyjmG9rRA5kf%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1767193199%26allow_ip%3D%26allow_referer%3D%26signature%3DfvDkHaLPNZbH6ExLZ2vwOwTWDps%253D)


