본 글은 [SW Expert Academy]의 파이썬 SW문제 해결 응용-구현2 완전 검색 강의를 보고 정리한 글입니다
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
그래프의 최소 비용 문제
목차
01 최소 신장 트리
02 프림 알고리즘
03 크루스칼 알고리즘
04 최단 경로
05 다익스트라 알고리즘
01 최소 신장 트리
그래프에서 최소 비용 문제 유형
1. 최소 *신장 트리 문제
가중치 그래프에서 모든 정점들을 연결하는 간선들의 가중치의 합이 최소가 되는 트리를 찾는 문제
*신장 트리란(Spanning Tree)?
N개의 정점을 포함하는 무향 그래프에서 N개의 정점과 N-1개의 간선으로 구성된 트리
*최소 신장 트리란(Minimum Spanning Tree)?
: 간선에 가중치를 줘서 신장 트리를 구성하는 간선의 가중치의 합이 최소인 신장 트리
-> 최소 신장 트리를 찾는 알고리즘: 프림, 크루스칼 알고리즘
2. 최단 경로 문제
시작 정점에서 목표 정점까지 가는 간선의 가중치의 합이 최소가 되는 경로를 찾는 문제
02 프림 알고리즘
프림 알고리즘(Prim's Algorithm)
한 정점에 연결된 간선들 중 최소 간선을 가진 정점을 선택해나가며 최소 신장 트리를 만들어가는 방식
프림 알고리즘의 동작과정
1. 임의의 정점을 하나 선택해서 시작
2. 선택한 정점들과 인접하는 정점들 중에 최소 비용의 간선이 존재하는 정점을 선택
3. 선택한 간선의 개수가 n-1개가 될 때 까지 이를 반복(단, 정점의 개수는 n개)
프림 알고리즘을 동작하기 위해 필요한 정보
: 두 종류의 상호 배타 집합(2 disjoint-sets)에 관한 정보
트리 정점(Tree vertices)
최소 신장 트리를 만들기 위해 선택된 정점
비트리 정점 (non-tree verticies)
선택되지 않은 정점
코드
pseudo code
MST_PRIM(G,r) // G : graph, r : start vertex
/* initialize U.key and U.parent */
FOR ALL u in G.v // G.v : set of vertecies
u.key = MAX_VALUE // u.key : u is a edge that minimum weight connected to U
u.parent = NULL // u.parent : parent of U in tree
r.key = 0
Q = G.v // put in Q, all the vertecies (Q is priority queue)
WHILE Q is not empty
u = Extract_MIN(Q) // bring key that has minimum value in Q
FOR ALL v in ADJ(G,u) // ADJ : Adjacent vertecies
IF v in Q AND weight(u,v) < v.key
v.parent = u
v.key = weight(u,v) // renew the distance with treeIn python,
# G : 그래프, r : 시작 정점
def MST_PRIM(G, s):
key = [INF] * N # 가중치를 무한대로 초기화
pi = [None] * N # 트리에서 연결될 부모 정점 초기화
visited = [False] * N # 방문 여부 초기화
key[s] = 0 # 시작 정점의 가중치를 0으로 설정
for _ in range(N): # 정점의 개수만큼 반복
minIndex = -1
min = INF
for i in range(N): # 방문 안한 정점 중 최소 가중치 정점 찾기
if not visited[i] and key[i] < min:
min = key[i]
minIndex = i
visited[minIndex] = True # 최소 가중치 정점 방문처리
for v, val in G[minIndex]: # 선택 정점의 인접한 정점
if not visited[v] and val < key[n]
key[v] = val # 가중치 갱신
pi[v] = minIndex # 트리에서 연결될 부모의 정점*해당 함수 종료 시, parent(코드에서 pi)에 저장되어 있는 정보가 최소 신장 트리에 해당
03 크루스칼 알고리즘
크루스칼 알고리즘(Kruskal Algorithm)
최소 가중치 간선을 하나씩 선택해서 최소 신장 트리를 찾는 알고리즘
- N개의 정점을 포함하는 그래프에서 n-1개의 간선을 선택하는 방식
- 간선을 선택해 나가는 과정에 여러 개의 트리들이 존재
* 단, 사이클이 생기지 않아야 함
- 간선을 선택할 경우 간선의 두 정점이 속한 트리가 연결되어 하나의 집합이 됨.
- 이 때 이 두 정점이 이미 연결된 트리에 속하는 정점이면 사이클이 생김
크루스칼 알고리즘의 동작과정
1. 최초 모든 간선을 가중치에 따라 오름차순으로 정렬
2. 가중치가 가장 낮은 간선부터 선택하면서 트리를 증가시킴
3. 사이클이 존재하면 다음으로 가중치가 낮은 간선 선택
4. n-1 개의 간선이 선택될 때까지 앞의 과정 반복
코드
pseudo code
MST_KRUSKAL(G)
T = empty_set
FOR ALL v in G.v
Make_set(v)
sort(G.e.start, G.e.end) // default is ascending order
WHILE T.size() < |V| - 1
u = Extract_MIN(G.e) // choose the edge that has minimum weight
IF Find_set(U) != Find_set(v)
T = T UNION {(u,v)}
Union(u,v)
RETURN TIn Python,
def MST_KRUSKAL(G):
mst = []
for i in range(N):
Make_Set(i)
G.sort(key=lambda t:t[2])
mst_cost = 0
while len(mst) < N-1:
u, v, w = G.pop(0)
if Find_Set(u) != Find_Set(v): #check cycle
Union(u,v)
mst.append((u,v))
mst_cost += val
크루스칼 알고리즘의 특징
간선 선택 과정에서 생성되는 트리를 관리하기 위해 *상호 배타 집합 사용
- 트리에 속한 노드들을 자신을 루트로 하는 서브 트리의 높이를 랭크(Rank)라는 이름으로 저장
선택한 간선으로 두 개의 트리가 한 개의 트리로 합쳐질 때 각 트리에 해당하는 상호 배타 집합을 Union연산으로 합침
- 랭크 값이 작은 트리를 랭크 값이 큰 트리의 서브 트리로 포함시키게 되면 트리에 포함된 노드들의 랭크 값을 수정할 필요가 없음
04 최단 경로
최단 경로 문제(Shorthest Path Problem)
간선의 가중치가 있는 유향 그래프에서 두 정점 사이의 경로들 중에 간선의 가중치의 합이 최소인 경로
문제 유형
| 단일 시작점(출발점-다른 모든 정점들에 이르는 최단 경로 문제) | 모든 쌍(모든 정점 쌍 간의 최단 경로) |
| 다익스트라 알고리즘(음의 가중치 X) | 플로이드-워샬 알고리즘 |
| 벨만 포드 알고리즘(음의 가중치O, 음의 사이클X) |
05 다익스트라 알고리즘
다익스트라 알고리즘(Dijkstra's Algorithm)
- 시작 정점에서 거리가 최소인 정점부터 선택해 나가면서 최단 경로를 구하는 방식
- 탐욕 기법을 사용한 알고리즘으로 최소신장 트리를 구하는 프림 알고리즘과 유사
- 시작 정점(r)에서 끝 정점(t)까지의 최단 경로에 정점x가 존재
- 즉, 최단 경로는 r에서 x까지의 최단경로와 x에서 t까지의 최단 경로로 구성
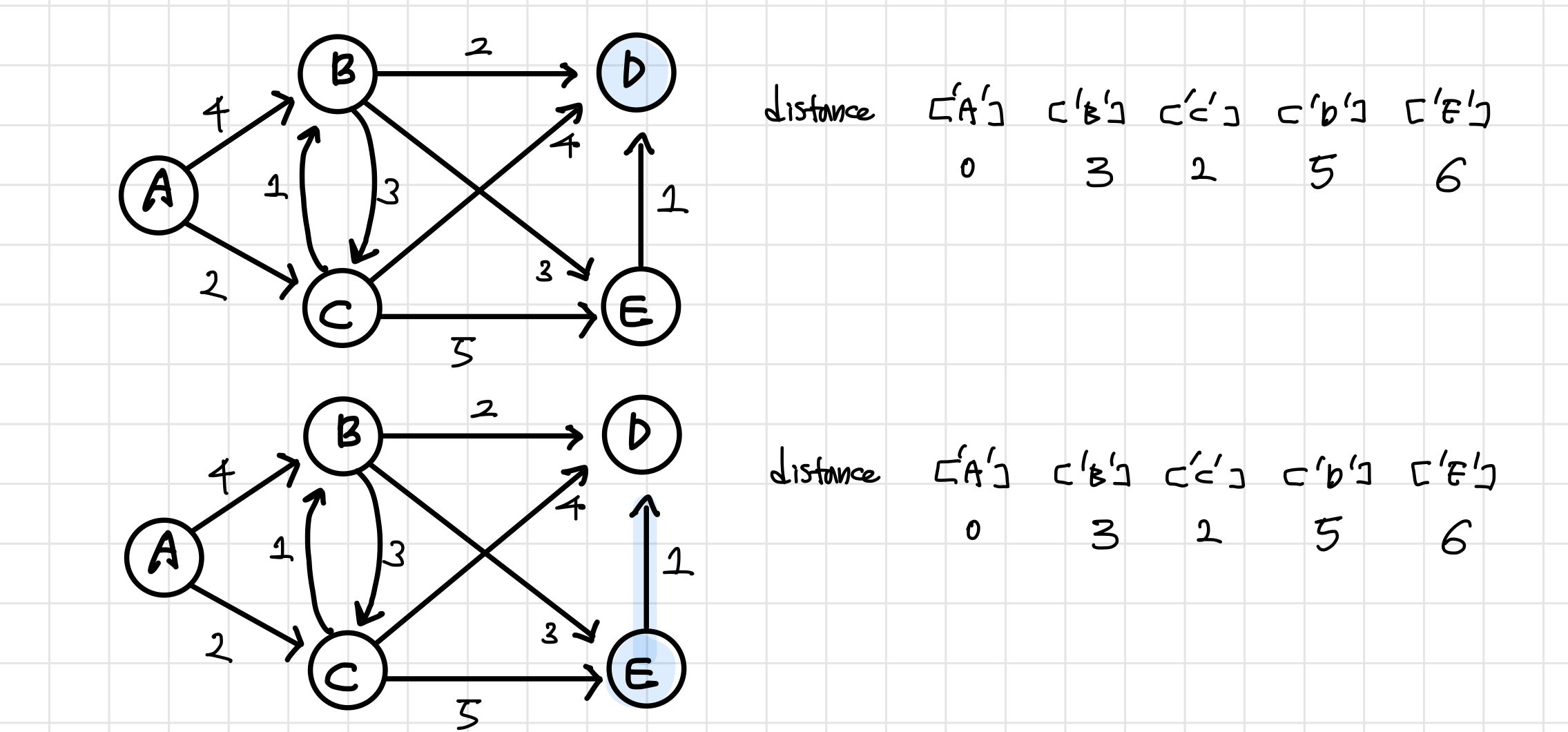
탐욕적 방법으로 정점 선택하기(예시)

1. 시작 노드 s의 거리 0으로 설정(s='A')
- 나머디 노드는 inf로 초기화

2. distance에서 가장 최소 값을 가지는 노드 u방문(min(dist) = 'A')
- 방문 노드의 인접 노드 v거리 확인
- dist[v] > dist[u] + w(u,v) 이면 dist[v] = dist[u] + w(u,v)로 갱신



코드
pseudo code
// G : graph, r : start vertex, s : set of chosen vertecies
// D : distance for all chosen vertecies weight == value of minimum path
// P : Minimum Path tree
// ADJ(u) : adjacent vertecies at U
Dijkstar(G,r)
s = empty_set // initialize set S
FOR ALL v in V
D[v] = MAX_VALUE
P[v] = NULL
D[r] = 0
WHILE S != V
select u in V-S that Vertex has minimum D[u]
S = S UNION {u}
FOR ALL v in ADJ(u)
IF v in V - S and D[u] + weight(u,v)
D[v] = D[u] + weight(u,v)
P[v] = uIn python,
def Dijkstra(G,s):
dist = [INF] * N
path = [None] * N
visited = [False] * N
dist[s] = 0
for _ in range(N):
minIdx = -1
min = INF
for i in range(N):
if not visited[i] and dist[i] < min:
min = dist[i]
minIdx = i
visited[minIdx] = True
for v, w in G[minIdx]:
if not visited[v] and dist[minIdx] + w < dist[v]:
dist[v] = dist[minIdx] + w
path[v] = minIdx
음의 가중치가 있을 경우
- 이미 선택한 정점에 대해서는 다시 방문하지 않으므로, 이후 음의 가중치가 있어도 방문한 노드일 경우 이를 갱신하지 못함
- 즉, 음의 가중치가 있을 경우 다익스트라 알고리즘으로는 최단 경로를 찾을 수 없음
벨만-포드 알고리즘(Bellman-Ford's Algorithm)
- 음의 가중치를 포함하는 그래프에서 최단 경로를 구할 수 있음
- 단 음의 싸이클은 허용하지 않음
- 다익스트라와 다르게 한 번 방문한 노드도 다시 방문 -> $O(n^3)$
- 다익스트라는 $O(n^2)$
'Algorithm > SW Expert Academy' 카테고리의 다른 글
| [SWEA] 분할 정복(Divide and Conquer) (0) | 2022.03.13 |
|---|---|
| [SWEA] 완전 검색(Brute-force search) (0) | 2022.02.26 |
| [SWEA] 그래프의 기본과 탐색 (0) | 2020.09.15 |
| [SWEA] 탐욕 알고리즘(Greedy Algorithm) (0) | 2020.09.08 |
| [SWEA] 동적 계획법(Dynamic Programming) (0) | 2020.08.18 |
![[SWEA] 그래프의 최소 비용 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fcwj5Ph%2FbtqJs5ceBPh%2FAAAAAAAAAAAAAAAAAAAAAHqM_7dNlV64PIolyof1A5qTGsMkBl6LEWa5EJpoKnLB%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DwJR%252FzVdcY4R6Y4LFC3hhNoInXXE%253D)