본 글은 [SW Expert Academy]의 파이썬 SW문제 해결 응용-구현 그래프의 기본과 탐색 강의를 보고 정리한 글입니다
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
그래프의 기본과 탐색
목차
01 그래프 기본
02 그래프 탐색
03 상호배타 집합들
01 그래프 기본
그래프(Graph)란?
객체들과 이들 사이의 연결 관계를 표현하는 것으로 정점(Vertex/Node)들의 집합과 이들을 연결하는 간선(Edge)들의 집합으로 구성된 자료구조
- G = (V,E), V: 정점들의 집합, E: 간선들의 집합
- |V|: 정점의 개수, |E|: 그래프에 포함된 간선의 개수
- |V|개의 정점을 가지는 그래프는 최대 |V| (|V|-1)/2 개 간선이 가능
- 선형 자료구조, 트리 자료구조로 표현하기 어려운 다대다(N:N) 관계를 가지는 원소들을 표현하기에 용이
그래프의 종류

무향 그래프(Undirected Graph)
: 서로 대칭적인 관계를 연결해서 나타낸 그래프
유향 그래프(Directed Graph)
: 간선을 화살표로 표현, 방향성의 개념이 포함됨
가중치 그래프(Weighted Graph)
: 이동하는데 드는 비용을 간선에 부여한 그래프
그래프 용어(term)
인접(Adjacency)
: 두 개의 정점이 간선으로 연결되면 서로 인접해 있다고 함
*무향 그래프와 유향 그래프에서의 인접 정점의 기준은 다름.
- 무향 그래프: 간선에 방향성이 없으므로 하나에 간선에 연결된 두 정점은 반드시 인접 정점임
- 유향 그래프: 간선에 방향성이 있으므로 1->2 일 경우, 2번 정점은 1번의 인접정점이나, 1번 정점은 2번 정점의 인접정점이 아님
*완전 그래프 : 모든 정점들이 서로 인접해 있는 그래프
*부분 그래프 : 원래 그래프에서 일부의 정점이나 간선을 제외한 그래프
경로
: 간선들을 순서대로 나열 한 것
- ex : 간선(0,2), (2,4), (4,6) 경로: 0->2->4->6
- 단순 경로 : 경로 중 한 정점을 최대한 한 번만 지나는 경로
- 사이클 : 시작한 정점에서 끝나는 경로
- 사이클이 없는 유향 그래프(DAG, Directed Acyclic Graph)
그래프 표현
간선의 정보를 저장하는 방식, 메모리나 성능을 고려해서 결정
인접 행렬 (Adjacent Matrix)
: |V|x|V| 크기의 정방 행렬로, 2차원 배열을 이용해서 간선 정보를 저장

- 행 번호와 열 번호는 그래프의 정점에 대응하며 두 정점이 인접되어 있으면 1, 그렇지 않으면 0으로 표현
- 단점: 정점의 개수 n이 커지면 필요한 메모리 크기는 에 비례해서 커짐-> 인접 리스트로 해결 가능
인접 리스트 (Adjacent List)
: 각 정점마다 인접 정점으로 나가는 간선의 정보를 연결리스트에 저장
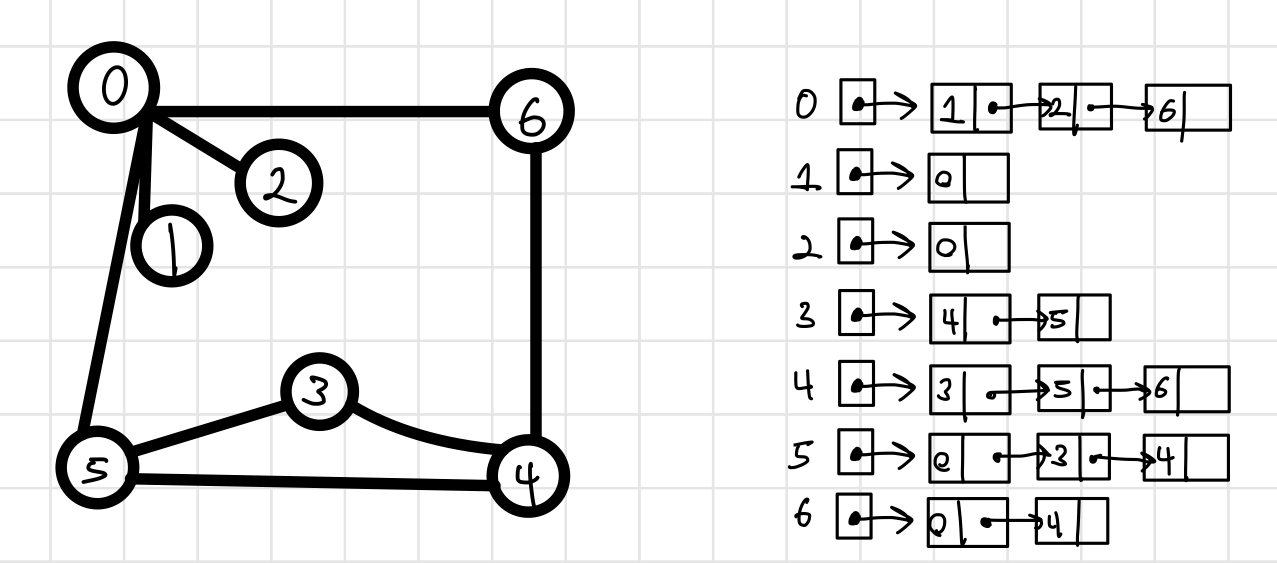
- 각 정점에 대한 인접 정점을 개수만큼 저장하고 각각 노드로 하는 리스트로 저장함
- 노드 수 = 간선의 수, 각 정점의 노드 수 = 정점의 진출 차수
- 장점: 불필요한 메모리 사용과 비용 절감 가능
- 상대적으로 간선의 수가 적을 때 사용하는 방법
02 그래프 탐색
그래프 순회
: 비선형적 구조인 그래프로 표현된 모든 정점을 빠짐없이 탐색하는 것으로 대표적으로 깊이 우선 탐색(Depth First Search, DFS), 너비 우선 탐색 방법(Breadth First Search, BFS)이 있다
깊이 우선 탐색(DFS)
- stack, 재귀호출을 사용하여 구현
DFS 알고리즘(재귀)
# G: Graph, v: start vertex
# G[v] : v's adjacency list
# |V|: # of vertex
visited = [False] * |G|
def DFS(G,v):
if visited[v]:
return
visited[v] = True
for w in G[v]:
DFS(G, w)Example:
Input:
A
/ \
B C
/ / \
D E FOutput:
A, B, D, C, E, F
너비 우선 탐색(BFS)
- queue를 사용하여 구현
- BFS를 활용하여 최단거리를 구할 수 있음
BFS 알고리즘
# G: Graph v: start vertex
# Q : queue
# G[v]: v's adgacency list
# |V| : # of vertex
visited = [False] * |V|
Q = list()
def BFS(Q,v):
Q.append(v)
visited[v] = True
while Q:
v = Q.pop(0)
for w in G[v]:
if not visited[w]:
Q.append(w)
visited[w] = TrueExample:
Input:
A
/ \
B C
/ / \
D E FOutput:
A, B, C, D, E, F
03 상호배타 집합들
상호배타 집합들(서로소)이란?
: 서로 중복 포함된 원소가 없는 집합, 교집합이 없는 집합
상호배타 집합 연산
Make-Set(x): 원소 x만으로 구성된 집합을 생성하는 연산
Find-Set(x): 임의의 원소 x가 속한 집합을 알아내기 위해 사용하며, *집합의 대표자를 알기 위한 연산
Union(x,y): x원소가 속한 집합과 y원소가 속한 집합을 하나의 집합으로 합치는 연산
*집합의 대표자: 집합을 구분하는 특정 원소를 대표자라고 함
표현 방법
연결 리스트
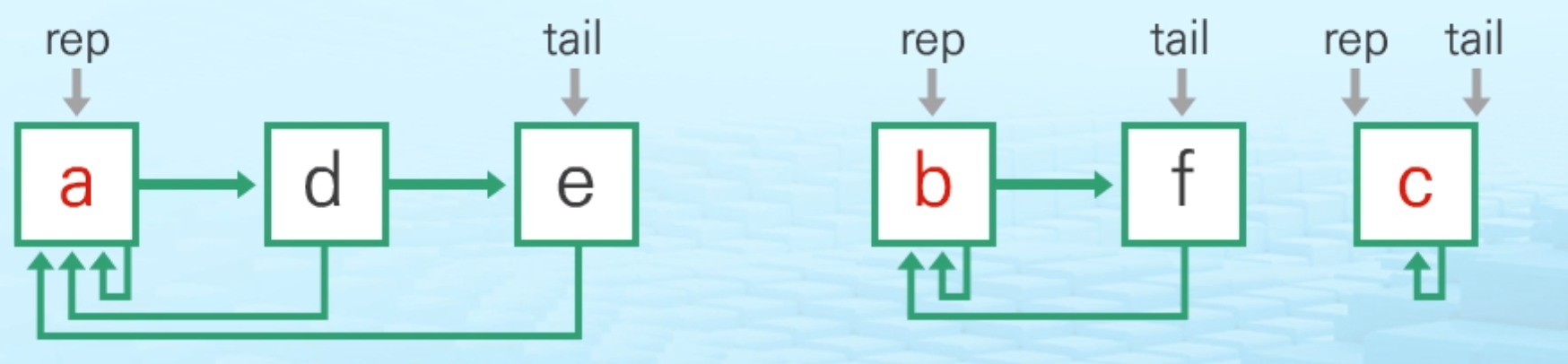
- 같은 집합의 원소들은 하나의 연결리스트로 관리함
- 연결리스트의 첫 번째 원소를 집합의 대표 원소로 삼음
- 각 원소는 집합의 대표 원소를 가리키는 링크를 가짐
연결리스트 연산
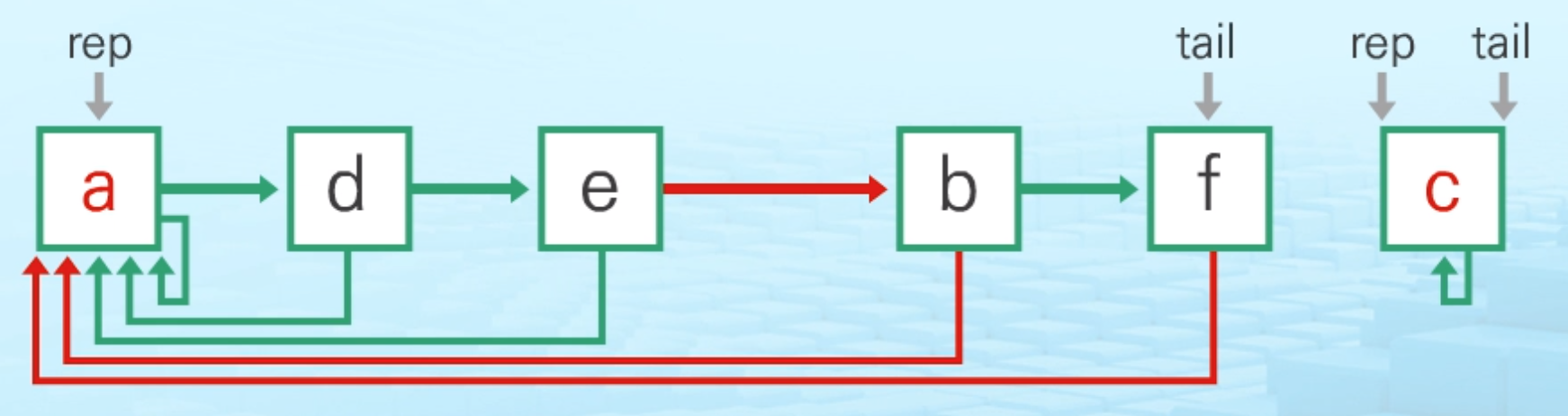
- Find-set(e): return a
- Find-set(c): return b
- Union(a,b): 크기가 작은 집합을 큰 집합의 뒤에 연결(연산속도 유리)
트리
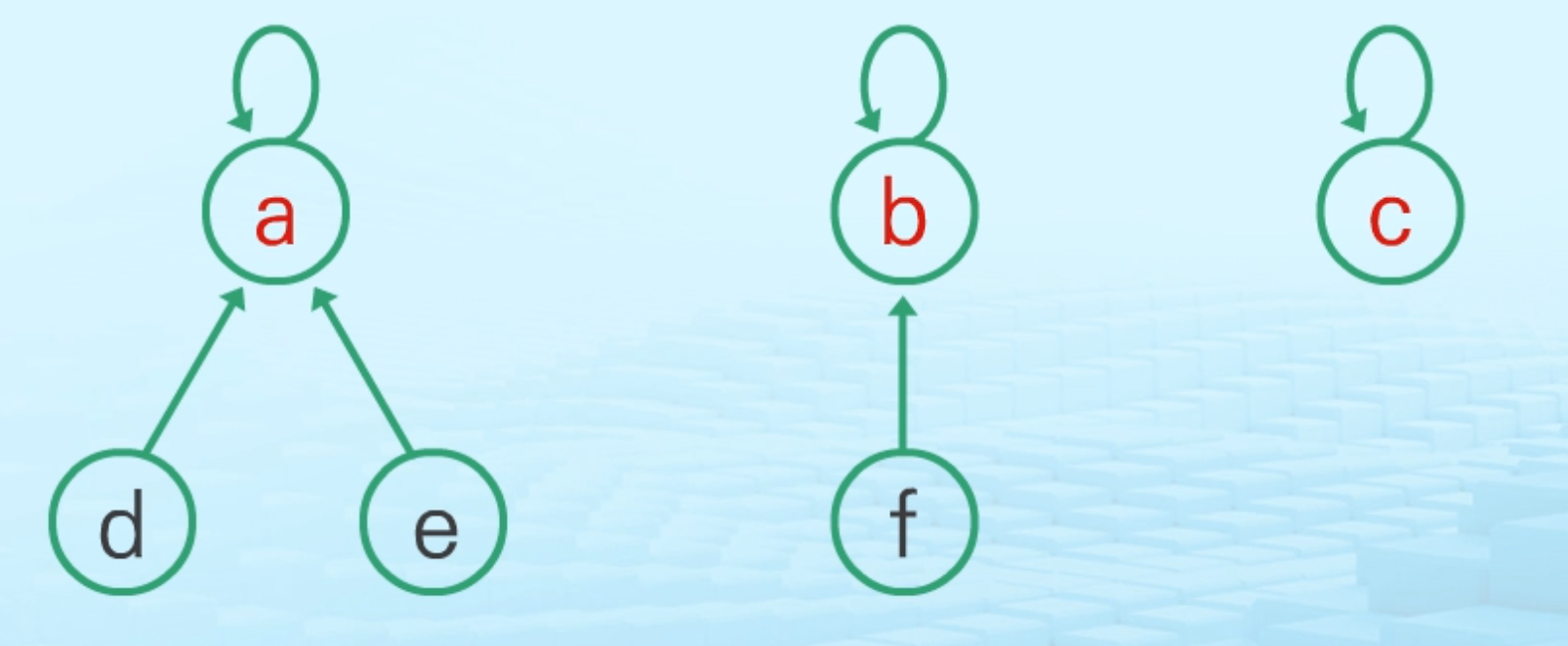
- 하나의 집합(a disjoint set)을 하나의 트리로 표현
- 자식 노드가 부모 노드를 가리키며 루트 노드가 집합의 대표자가 됨
- 연결 리스트보다 효율적이나, *편향 트리 구조가 될 가능성이 있음
*때문에 연산의 효율을 높이는 방법으로 Rank를 이용한 Union방식, Path compression등이 있음
트리 연산


*find-set연산 시, 자기 자신을 부모로 가리키는 원소를 찾을 때까지 탐색
'Algorithm > SW Expert Academy' 카테고리의 다른 글
| [SWEA] 그래프의 최소 비용 문제 (1) | 2022.05.16 |
|---|---|
| [SWEA] 분할 정복(Divide and Conquer) (0) | 2022.03.13 |
| [SWEA] 완전 검색(Brute-force search) (0) | 2022.02.26 |
| [SWEA] 탐욕 알고리즘(Greedy Algorithm) (0) | 2020.09.08 |
| [SWEA] 동적 계획법(Dynamic Programming) (0) | 2020.08.18 |
![[SWEA] 그래프의 기본과 탐색](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcouadN%2FbtqIPQUeQg9%2FdJDCPAc3etsqZJ1S7kpuZ1%2Fimg.png)