반응형
4. Logistic Regression(Classification)
목차
4-1. 로지스틱 회귀(분류)와 모델 설계
1. 로지스틱 회귀(분류)
2. 가설 설계
3. 결정 경계
4-2. 비용 함수
1. 로지스틱 회귀와 비용함수
2. 단순화된 비용 함수와 경사 하강법
3. 고급 최적화 기법
4. 크로스 엔트로피
4-3. 다중 레이블 분류: one-vs-all
4-1. 로지스틱 회귀(분류)와 모델 설계
1. 로지스틱 회귀(분류)
로지스틱 회귀(logistic regression)란?
- 샘플이 특정 클래스에 속할 확률을 추정
- 추정된 확률이 50%이상이면 샘플이 해당 클래스에 속한다고 예측함
- 예시: 스팸/햄 메일, 악성/양성 종양
분류기의 종류
- 이진 분류기(Binary Classifier)
- 두 개 클래스를 구분
- $y \in \{0,1\}$
- 다중 클래스 분류기(Multiclass classifier)
- 세 개 이상의 클래스를 구분
- $y \in \{0,1,2,3\}$
2. 가설설계
로지스틱 회귀의 가설설계(Hypothesis)
- 직선 모델 설계 시 이상치(outlier)를 예측하지 못하는 문제점이 생김
- 따라서, 시그모이드 함수(sigmoid function, 또는 로지스틱 함수(logistic functtion))을 이용하여 예측
- $h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-(\theta^Tx)}}$
- 이때, $g(z)$가 시그모이드 함수이며, $g(z)=\frac{1}{1+e^{-z}}$이다
- z에는 선형회귀식 $\theta^Tx$를 넣는다

시그모이드 함수
- 이 경우, x의 크기가 매우 커도 $h_\theta(x)$는 이상치에 영향을 적게 받는다(즉, robust하다)
- $h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-(\theta^Tx)}}$
로지스틱 회귀의 가설 결과 해석하기
- $h_\theta(x)$= (입력 x에 대해 y=1일 확률)
- 예시
- 만약 $x = \begin{bmatrix} x_0 \\ x_1 \end{bmatrix} = \begin{bmatrix} 1 \\ TumorSize \end{bmatrix}$
- $h_\theta(x)=0.7$인 경우 환자에게 "악성 종양일 확률이 70%입니다"라고 말함
- $h_\theta(x)=P(y=1|x;\theta)$
- x와 파라미터 $\theta$가 주어졌을 때, y=1일 확률
- $P(y=0|x;\theta)+P(y=1|x;\theta)=1$, (여기서 h는 이진분류에 해당)
- 즉 $P(y=0|x;\theta)=1-P(y=1|x;\theta)$
3. 결정경계
로지스틱 회귀
- $h_\theta(x)=g(\theta^Tx)=P(y=1|x;\theta)$
- $g(z)=\frac{1}{1+e^{-z}}$

- 위 그래프에서 결정경계는 z=0 이다
- 즉, $h_\theta >= 0.5$이면, y=1로 예측하고, $h_\theta < 0.5$이면 y=0으로 예측
결정 경계
- $h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2)$

비선형 결정 경계(Non-linear decision boundary)
- $h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_2^2)$

- 추가로 $h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_1^2x_2+\theta_3x_1x_2^2+\theta_4x_1^2x_2^2)$ 의 경우 아래와 같은 모양을 띔
4-2. 비용함수
1. 로지스틱 회귀와 비용함수
선형 회귀
- $J(\theta)=\frac{1}{2m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i)^2$
- 평균제곱오차(Mean Squared Error, MSE)로 표현
로지스틱 회귀
- $J(\theta)=\frac{1}{m} \sum_{i=1}^{m}Cost(h_{\theta}(x^i),y^i)$
- MSE를 사용하지 않음
- 비용 함수 조건(Cross Entropy, loss function): Convex, 확률 개념

- non-convex의 경우 지역 최소값(local minimum)에 빠질 수 있음
$
Cost(h_\theta(x),y) =
\begin{cases}
-log(h_\theta(x)) & \text{if y = 1}\\
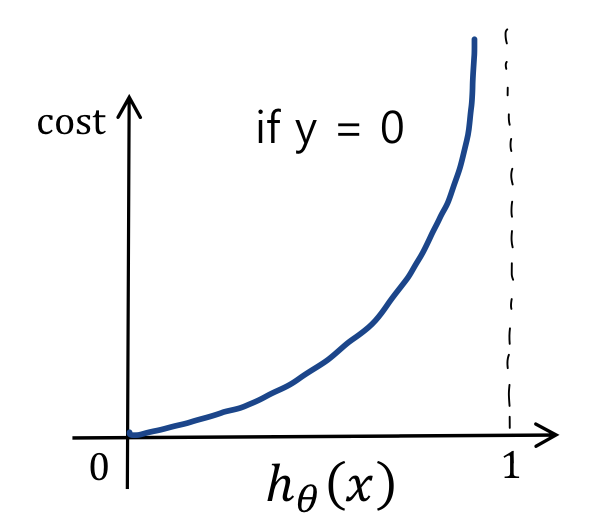
-log(1-h_\theta(x)) & \text{if y = 0}
\end{cases}
$
- $y = 1 \& h_\theta(x) = 1$이면, cost = 0이다. 그러나 as $h_\theta(x) \to 0, cost \to \infty$ 임
- 따라서, y = 1인데 $h_\theta(x)=0$이면, 비용이 매우 커지므로 학습 알고리즘은 이를 줄이는 방향으로 파라미터를 조정하게 됨
-

- 즉, $p(y=1|x, \theta)=0$에서 $\theta$를 조절하는 방향으로 가게 된다
-
- 마찬가지로, y = 0인데 $h_\theta(x)=1$이면, 비용이 매우 커지므로 학습 알고리즘은 이를 줄이는 방향으로 파라미터를 조정하게 됨
-
- 아래는 y=0, y=1일 때 두 그래프를 겹쳐 그린 형태이다
2. 단순화된 비용 함수와 경사 하강법
비용 함수 단순화 시키기
- $J(\theta)=\frac{1}{m} \sum_{i=1}^{m}Cost(h_{\theta}(x^i),y^i)$
- $
Cost(h_\theta(x),y) =
\begin{cases}
-log(h_\theta(x)) & \text{if y = 1}\\
-log(1-h_\theta(x)) & \text{if y = 0}
\end{cases}
$ - 언제나 y = 0 or y = 1
- 즉 위의 식을 간단하게 하면 $Cost(h_\theta(x),y) = -ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))$ 임
- if y = 1, $Cost(h_\theta(x),1) = -log(h_\theta(x))$
- elif y = 0, $Cost(h_\theta(x),0) = -log(1-h_\theta(x))$
$J(\theta)=\frac{1}{m} \sum_{i=1}^{m}Cost(h_{\theta}(x^i),y^i)=\frac{1}{m}[ \sum_{i=1}^{m} y^i log(h_\theta(x^i))+(1-y^i)log(1-h_\theta(x^i))]$
- 위의 식에서 파라미터를 구하려면 : $min_\theta J(\theta)$
- 새로운 데이터 샘플 x가 주어졌을 때 예측하려면: $h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}$
- $h_\theta(x) >= 0.5$ 인 경우 label을 1로 예측
- $h_\theta(x) < 0.5$인 경우 label을 0으로 예측
- 경사하강법 적용
- 비용함수(cost function)를 최소화 하는 $\theta$를 업데이트 하는 방법
- $\theta_j = \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta)$을 수렴할 때까지 반복
- $\frac{\partial}{\partial\theta_j}J(\theta)$을 미분시 아래와 같음
- $\frac{\partial}{\partial\theta_j}J(\theta)= \frac{1}{m} \sum_{i=1}^{m}(h_\theta (x^i) - y^i)x_j^i$
- 자세한 미분 과정은 아래 참고(참고 $\theta^T$는 $\theta$의 전치 행렬)
- 즉 선형 회귀의 $\theta$ 업데이트 식과 같다!
3. 고급 최적화 기법
- Momentum
- nesterov momentum
- AdaGrad
- RMSProp
- Adam
4. 크로스 엔트로피
정보 엔트로피(Information entropy, 또는 섀넌 앤트로피(Shannon entropy))
- 정보 이론(Information Theory)
- 시그널에 존재하는 정보의 양을 측정하는 응용수학의 한 갈래
- 잘 일어나지 않는 사건은 자주 발생하는 사건보다 정보량이 많다는 것이 핵심아이디어이다
- 정보 이론에서 정보(Information)란, 주어진 이벤트에서 발생하는 놀라움의 양
- $I(E)=-log[Pr(E)]=-log(P)$로 표현
- 엔트로피(Entropy)
- 인코딩 시 문자별 비트 수, information/surprise 측정
- 즉, 특정한 확률 과정에서 생성된 정보의 평균(기댓값)이다
- $H(X)=E[I(X)]=E[-log(P(X))] = - \sum_{i=1}^{n} P(x_i)logP(x_i) $
- 크로스 엔트로피(Cross Entropy)
- 두 분포 P,Q가 얼마나 다른지. 실제 데이터 분포와 우리가 추측한 데이터 분포의 차이
- $H(p,q) = H(p) + D_{KL}(p || q)$
- 여기서 $D_{KL}(p || q)$는 쿨백-라이블러 발산(KL-divergence)로, 두 확률 분포 P,Q의 다름을 설명하는 함수
- $D_{KL}(p || q) = \sum_{i=1}^{n} P(x_i)log(\frac{p(x_i)}{q(x_i)}) $
- P,Q 두 확률 분포가 비슷하면 KL-divergence는 낮은 값을 가짐
- P,Q 두 확률 분포가 다르다면 KL-divergence는 높은 값을 가짐
- 실제 분포 P에 대해 알지 못하는 상태에서 모델링을 통하여 구한 분포인 Q를 통하여 P를 예측하기 위해 필요한 값으로 사용됨
- 즉, 두 확률 분포 P,Q 사이를 측정하는 지표
- 엔트로피는 하나의 확률분포에 대한 측정 지표이며 크로스 엔트로피는 두 확률 분포에 대한 측정 지표임
4-3. 다중 레이블 분류 : one-vs-all
다중 레이블 분류(Multi-class classification)
- 세 개 이상의 클래스를 구분
- 예시
- 이메일 태깅: 업무, 친구, 가족
- 의학적 판단: 정상, 감기, 도 깜
- 날씨: 맑음, 흐림, 눈, 비
- 이진 분류 vs. 다중 레이블 분류
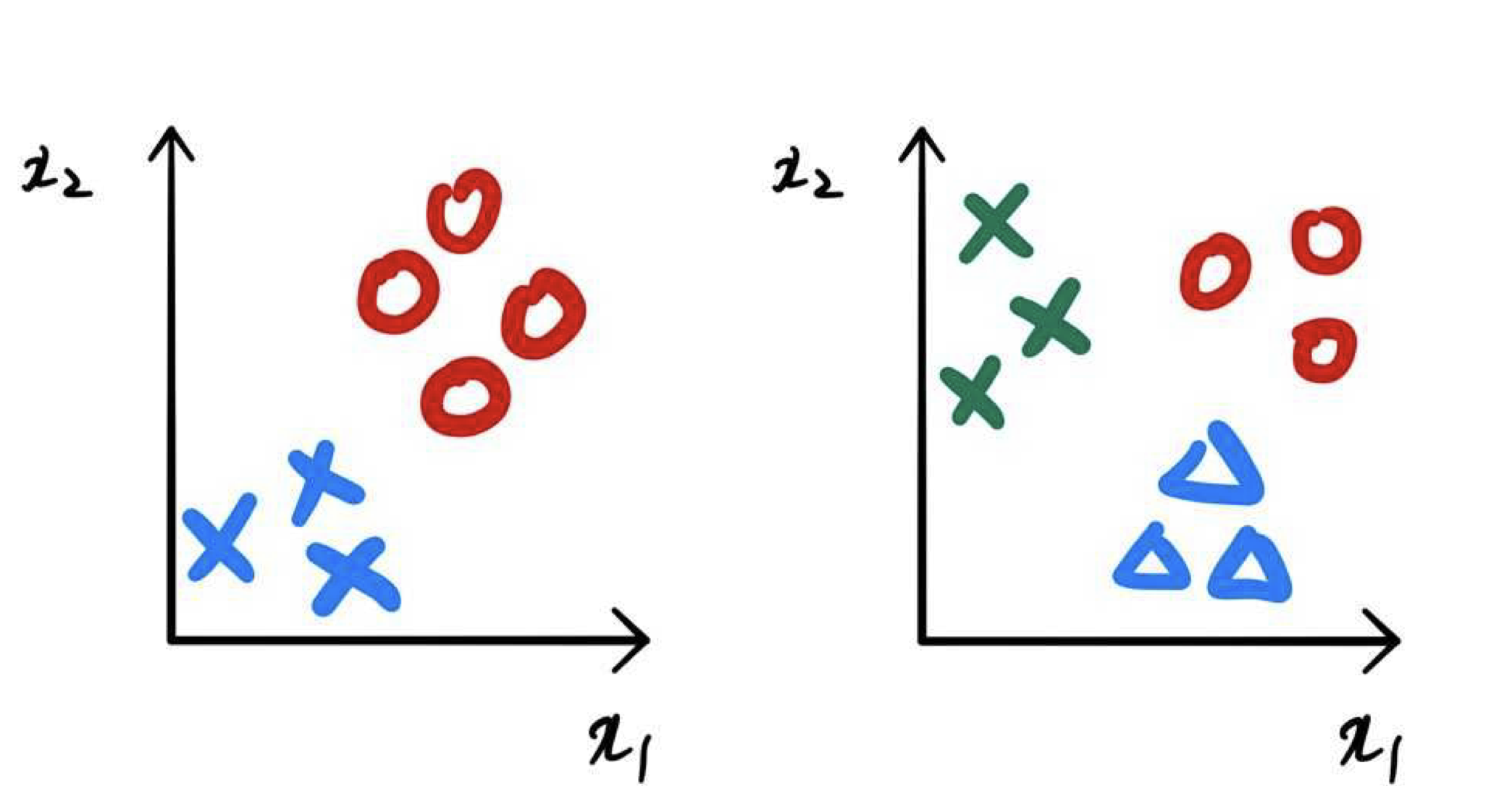
이진분류(좌), 다중분류(우)
일대다 분류 전략(one-vs-all, 또는 one-vs-rest)

- 각 클래스 i에 대해 로지스틱 회귀 분류기 $h_\theta^i(x)$를 학습시키고 y=i일 확률을 예측한다
- 새로운 입력 x에 대해, 다음을 최대화하는 클래스 i를 선택한다
- $max_i h_\theta^i (x)$
반응형
'인공지능(AI) > 머신러닝(ML)' 카테고리의 다른 글
| [핸즈온 머신러닝] 5. 정규화 (0) | 2021.12.05 |
|---|---|
| [핸즈온 머신러닝] 6장. 서포트 벡터 머신 (0) | 2021.12.05 |
| [핸즈온 머신러닝] 3장. 다항 선형 회귀 (0) | 2021.12.01 |
| [핸즈온 머신러닝] 2장. 단항 선형 회귀 (0) | 2021.11.18 |
| [핸즈온 머신러닝] 1장. 머신러닝 소개 (0) | 2021.11.16 |
![[핸즈온 머신러닝] 4장. 로지스틱 회귀(분류)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FsBSzh%2FbtrmTbNhyWb%2FAAAAAAAAAAAAAAAAAAAAAJrVIwZKW6qUNL3FdSztvb6O1unb2vvNI4As1I8mHKIR%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3D622XlBwOhSzbkxGjNgzn%252F7e0gcw%253D)