반응형
3. Linear Regression with multiple variables
목차
3-1. 다항 선형 회귀
1. 다항 선형 회귀란?
2. 2개 이상의 특성
3. 경사하강법
4. 특성과 다항 회귀
3-2. 정규 방정식
3-1. 다항 선형 회귀
1. 다항 선형 회귀란?
단항 선형 회귀(이전 게시글 참고)
https://codingsmu.tistory.com/111
[핸즈온 머신러닝] 2장. 단항 선형 회귀
2. Linear Regression with one variable 목차 1. 선형회귀란? 2. 모델설계 3. 비용 함수 4. 경사 하강법 1. 선형회귀란? 회귀(Regression) 연속적인 종속 변수와 한 개 이상의 독립 변수 사이의 관계를 추정하..
codingsmu.tistory.com
다항 선형 회귀란?
- Multivariate linear regression
- 두 개 이상의 특성을 추가하고, 확장된 특성을 포함한 데이터셋에 선형 모델을 훈련시키는 것
- 단항 선형 회귀($h_\theta(x) = \theta_0 + \theta_1x$) vs. 다항 선형 회귀(아래 식)
- $h_\theta(x) = \theta_0 + \theta_1x + \theta_2x_2$
- $h_\theta(x) = \theta_0 + \theta_1x + \theta_2x_1^2$
- $h_\theta(x) = \theta_0 + \theta_1x + \theta_2x_2 + \theta_3x_3 + ... $
2. 두 개 이상의 특성
기호 정리
- n = 특성의 개수
- $x^{(i)}$ = i번째 학습 예제의 입력(특성) $1<=i<=m$
- $x^{(i)}_j$ = i번째 학습 예제의 j번째 특성의 값 $1<=j<=n$
- 예시
-
집면적(제곱피트) 방 개수 층 수 연식 매매가(1000달러) 1500 4 25 1 2500 2500 8 26 1 3500 - 특성 개수(n) : 4개 -> x1(집면적), x2(방 개수), x3(층 수), x4(연식)
- $x^{(2)}$ = $ \begin{bmatrix} 1500 \\ 4 \\ 25 \\ 1 \\ 2500 \end{bmatrix}$
- $x^{(2)}_3 =26$
-
Hypothesis
- 단항 선형 회귀: $h_\theta(x) = \theta_0 + \theta_1x$
- 다항 선형 회귀: $h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + \theta_4x_4$
- 예시(위의 테이블 참고)
- $h_\theta(x) = 80 + 0.1x + 0.01x_2 + 3x_3 - 2x_4$
행렬과 벡터 곱으로 표현하기
- $h_\theta(x) = \theta_0 + \theta_1x + \theta_2x_2 + \theta_3x_3 + \theta_4x_4 = \theta^Tx$
- 즉, $h_\theta(x) = \theta^Tx$
- 유도과정은 아래 참고
- 더보기

3. 경사하강법
다항 선형 회귀에 대한 경사 하강법
- 가설(Hypothesis): $h_\theta(x) = \theta_0 + \theta_1x +... + \theta_nx_n$
- 파라미터(Parameter): $\theta_0, \theta_1, ..., \theta_n$
- 비용함수(Cost function)
- $J(\theta_0, \theta_1, ..., \theta_n)=\frac{1}{2m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i)^2$
- $J(\theta)$로도 표현
- 경사하강법(Gradient descent)
- 수렴할 때까지 아래 식을 반복
- $\theta_j = \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta_0, \theta_1, ..., \theta_n)$
n=1일 때 경사하강법(단항선형회귀) vs. n>=1일 때 경사하강법(다항)
경사하강법에 대한 조언
- Feature scaling(feature normalization)
- 여러 특성들을 유사한 크기로 맞추자

scaling 전(좌), scaling 후(우) - 예1) 모든 특성 값의 범위를 대략 $-1<=x_i<=1$ 범위로 만들자
- $x_1$: 면적(0~2000$ft^2$) , $x_2$: 방 개수(1~5개)
- $x_1=\frac{area(ft^2)}{2000}$, $x_2=\frac{rooms}{5}$
- 예2) Mean Normalization: $x_i$ 대신 $x_i - \mu$로 대체하여, 특성들의 평균을 대략 0으로 만들자
- 단, $x_0=1$에는 적용하지 않음
- $x_1=\frac{area-1000}{2000}$, $x_2=\frac{rooms-2}{5}$
- 단, $\mu_i$는 $x_i$의 평균
- 따라서 $-0.5<=x_i<=0.5, -0.5<=x_2<=0.5$
- 경사하강법 디버깅하기
- 경사하강법 디버깅이란, 경사하강법이 잘 작동하는지 확인하는 것으로 학습율(learning rate)을 결정하는 방법이다
- $\theta_j = \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta)$

- $J(\theta)$는 매반복마다 줄어들어야 함
- 수렴했음을 감지하는 규칙의 예) 1회 반복시 $J(\theta)$의 감소폭이 $10^{-3}$이하면 수렴했다고 봄
- 경사하강법이 잘 작동하고 있지 않은 경우

- learning rate $\alpha$가 너무 큰 경우-> 수렴하지 못함 -> 더 작은 $\alpha$를 사용하자
- 충분히 작은 $\alpha$를 사용하고 있는 경우, $J(\theta)$는 매 반복마다 줄어드는건 확실함
- 그러나 $\alpha$가 너무 작은 경우, 경사하강법은 너무 느리게 수렴하게 됨
- $\alpha$에 따른 반복횟수-J의 관계
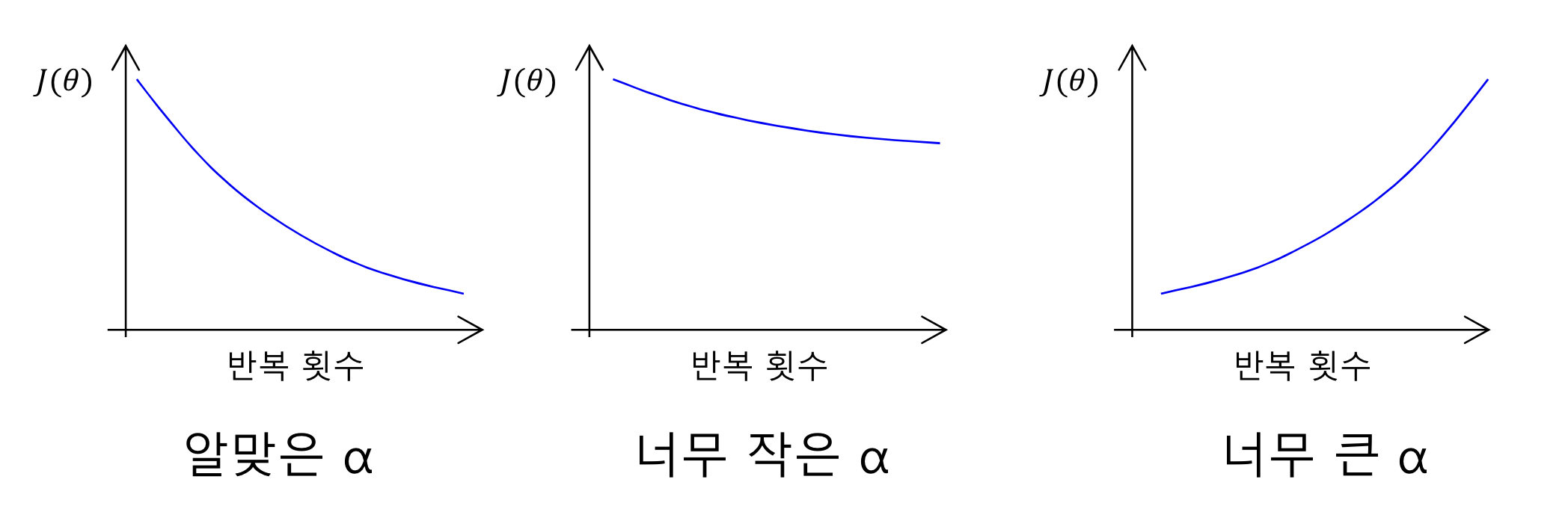
- 너무 작은 $\alpha$: 느린 수렴
- 너무 큰 $\alpha$: $J(\theta)$가 줄어들지 않을 수 있고, 아예 수렴하지 않을 수도 있음
- 보통 주로 쓰는 $\alpha$는 ..., 0.0001, 0.001, 0.01, 0.1, 1, ... 로 상황에 맞게 적절히 쓰면 된다
4. 특성과 다항 회귀
(예)집값 예측
- $h_\theta(x)= \theta_0+\theta_1*(width)+\theta_2*(depth)$
- 면적: $x=(width)*(depth)$
- $h_\theta(x)= \theta_0+\theta_1*x$
다항회귀

더 loose한 h(x) : 초록색/ 더 fit한 h(x): 파란색 - $h_\theta(x)= \theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3=\theta_0+\theta_1(size)+\theta_2(size)^2+\theta_3(size)^3$
- 특성 선택하기
3-2. 정규 방정식
정규방정식(Normal equation)이란?
$\theta$를 구하는 방법은 크게 수치적 방법(Numerical solution)과 해석적 방법(Analytical solution)이 있다. 앞서 배운 경사하강법은 수치적 방법에 해당하며, 지금부터 배울 정규 방정식은 해석적 방법에 해당한다 식은 아래와 같이 쓴다
$$NormalEquation= \theta = (X^TX)^{-1}X^Ty$$
예제(m=4)
| $x_0$ | 집면적 (제곱피트) |
방 개수 | 층 수 | 연식 | 매매가(1000달러) |
| 1 | 1500 | 4 | 25 | 1 | 2500 |
| 1 | 2500 | 8 | 26 | 1 | 3500 |
| 1 | 2400 | 5 | 10 | 3 | 3000 |
| 1 | 1400 | 3 | 13 | 12 | 1500 |
| ... | ... | ... | ... | ... |
- $y$ = $ \begin{bmatrix} 2500 \\ 3500 \\ 3000 \\ 1500 \\ ... \end{bmatrix}$
- $X$ = $ \begin{bmatrix} 1 && 1500 && 4 && 25 && 1 \\ 1 && 2500 && 8 && 26 && 1 \\ 1 && 2400 && 5 && 10 && 3 \\ 1 && 1400 && 3 && 13 && 12 \\ 1 && ... && ... && ... && ... \end{bmatrix}$
- $\theta = (X^TX)^{-1}X^Ty$ 유도 과정
- $X\theta=y$ , 양변에 $X^T$ 곱하기
- $X^TX\theta=yX^T$, 좌변에 $X^TX$를 없애기 위해 $(X^TX)^{-1}$양변에 곱하기
- $(X^TX)^{-1}X^TX\theta=yX^T(X^TX)^{-1}$, 이 경우 $(X^TX)^{-1}X^TX = 1$임
- $\theta = (X^TX)^{-1}X^Ty$
m개 학습 데이터, n개 특성인 경우
- $y$ = $ \begin{bmatrix} y^{(1)} \\ . \\ . \\ . \\ y^{(m)} \end{bmatrix}$
- $X$ = $ \begin{bmatrix} 1 && x^{(1)}_1 && x^{(1)}_2 && x^{(1)}_3 && ... && x^{(1)}_n \\ ... && ... && ... && ... && ... && ... \\ 1 && x^{(m)}_1 && x^{(m)}_2 && x^{(m)}_3 && ... && x^{(m)}_n \end{bmatrix}$
- $(X^TX)^{-1}$ 계산 시 시간복잡도
- $X^T=((n+1)*m)$이고, $X=(m*(n+1))$이므로
- $X^TX = O((n+1)(n+1)) = O(n^2 + 2n +1) = O(n^2)$
- $(X^TX)^{-1}$ 즉, inverse 계산까지 수행 시 총 시간복잡도는 $O(n^3)$가 걸리게 된다
경사하강법 vs. 정규방정식(m개 학습 데이터, n개 특성인 경우)
| 경사하강법 | 정규방정식 | |
| 장점 |
|
|
| 단점 |
|
|
반응형
'인공지능(AI) > 머신러닝(ML)' 카테고리의 다른 글
| [핸즈온 머신러닝] 6장. 서포트 벡터 머신 (0) | 2021.12.05 |
|---|---|
| [핸즈온 머신러닝] 4장. 로지스틱 회귀(분류) (0) | 2021.12.03 |
| [핸즈온 머신러닝] 2장. 단항 선형 회귀 (0) | 2021.11.18 |
| [핸즈온 머신러닝] 1장. 머신러닝 소개 (0) | 2021.11.16 |
| 경사하강법과 손실함수 (0) | 2021.05.21 |
![[핸즈온 머신러닝] 3장. 다항 선형 회귀](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fr1hJL%2FbtrmJjEnfPr%2FAAAAAAAAAAAAAAAAAAAAAF_30CbxAZyTOzoAZL3NNLYI7NDcWqrd0zjBcI5DRWO2%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DBAPTQIkfYHjVkfgiYgbztQVqLgo%253D)

