02 자연어처리를 위한 수학

목차
1. 확률의 기초(Probability)
1.1 확률변수
1.2 확률변수와 확률분포
1.3 이항분포, 다항분포, 정규분포
1.4 조건부 확률과 베이즈 정리
1.5 기댓값과 분산
2. 최대 우도 추정과 최대 사후 확률 추정(MLE & MAP)
2.1 MLE
2.2 MAP
3. 정보이론과 엔트로피(Information theory & entropy)
3.1 정보량
3.2 엔트로피
3.3 KL-Divegence, Preplexity
1. 확률의 기초(Probability)
1.1 확률변수
용어 정의
표본 공간(sample space) : 어떤 사건에서 발생할 수 있는 모든 경우의 수
확률변수(random variable) : 어떤 사건을 실수 표현으로 매핑하는 일종의 함수
사상(outcomes) : 표본 공간의 각각의 원소를 말함
용어 사용 예
시행(Experiment) : 두 개의 동전 던지기
사상(Outcomes): HH, HT, TH, TT
표본 공간(Sample space): {HH, HT, TH, TT}
사건(Event)
예1. 두 동전이 모두 앞면으로 나오는 경우 {HH}
예2. 적어도 한 개의 동전이 앞면으로 나오는 경우 {HH, HT, TH}
확률변수(Random variable)
예1. 사상 중 HH -> 숫자 2로 매핑 (확률변수 X = 2)
예1. 사상 중 HH -> 숫자 2로 매핑, HT&TH -> 숫자 1로 매핑 (확률변수 X = 2, X =1)
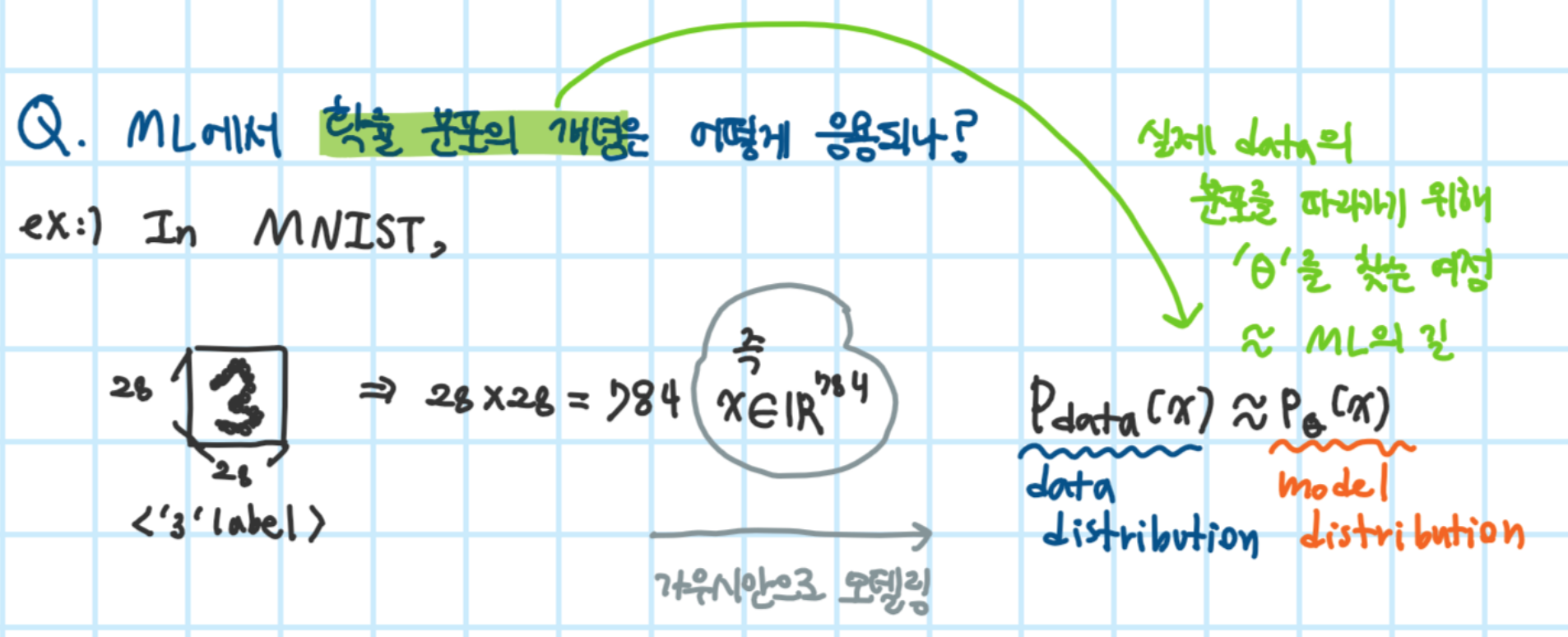
머신러닝(ML)에서 확률변수 사용 예
사람의 속성 표현

ML에서는 데이터를 일반적으로 확률 변수라 간주함
예) 이미지의 픽셀값, 문장의 단어 벡터(one-hot encoding)
1.2 확률변수와 확률분포
random variable이 discrete/continuous 에 따라 probability distribution이 PMF/PDF로 분류됨
1) 이산 확률 변수와 연속 확률 변수
이산적인 사건과 연속적인 사건을 표현하기 위해, 확률 변수에는 이산 확률 변수와 연속 확률 변수라는 개념이 존재함
이산 확률 변수(Discrete random variables)
확률질량함수 PMF : p(x) = P(X=x)
- 확률 변수 X가 취할 수 있는 값들이 이산적으로 셀 수 있는 경우
- 예) 공장에서 발생하는 불량품의 개수, 동전 하나를 던질 때 앞면이 나오는 횟수
연속 확률 변수(Continuous random variables)
누적분포함수 CDF : p(x) = P(X<=x)
확률밀도함수 PDF : p(x) = f(x)를 a~b로 적분한 값
- 확률 변수 X가 취할 수 있는 값들이 어떤 범위(연속된)로 주어지는 경우
- 예) 사람의 키, 체중 등
확률 분포(Probability distribution)
- 확률변수가 특정한 값을 가질 확률을 나타내는 함수
2) 이산 확률 분포(Discrete probability distribution)
- 확률 변수가 이산 확률 변수일 때 확률 분포
예) 동전 두 개를 던지는 시행에서 나오는 앞면의 수를 이산 확률 변수 X라 하면, 이산 확률 분포는 아래와 같음

확률 질량 함수(Probability mass function : PMF)
이산 확률 변수 X가 임의의 실수 x의 값을 취할 확률을 나타내는 함수
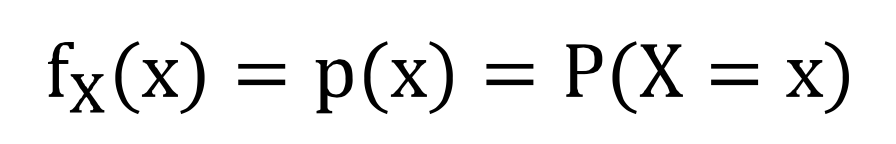
- 동전 하나 던질 때 앞면이 나오는 확률 : P(X = 1) = 1/2
3) 연속 확률 분포
- 확률변수가 연속 확률 변수일 때 확률 분포
예1) 수리 기사가 고장난 기계를 고치는데 걸리는 시간을 X라고 할 때, 기사가 30분안에 기계를 고칠 확률이 70%인 것은 아래처럼 나타낼 수 있음
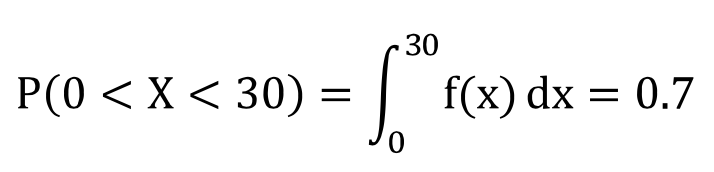
- 확률 변수 X가 a와 b 사이에 놓일 확률은 그 구간의 적분을 통해 구할 수 있음
*아래는 f(x)를 그래프로 나타낸 것

확률 밀도 함수 (Probability density function : PDF)
- X에서의 확률이 아닌 상대적인 밀도를 나타냄
- 확률 밀도 함수도 확률 질량 함수처럼 확률의 특성을 지녀야 하므로, 모든 확률 변수에 대한 확률의 합은 1
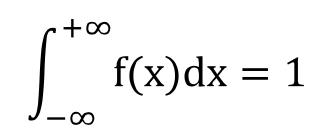

예2) 우리나라 사람의 키를 X라 할 때, 키가 180보다 작은 사람들이 전체 인구의 90%인 것은 아래처럼 나타낼 수 있음
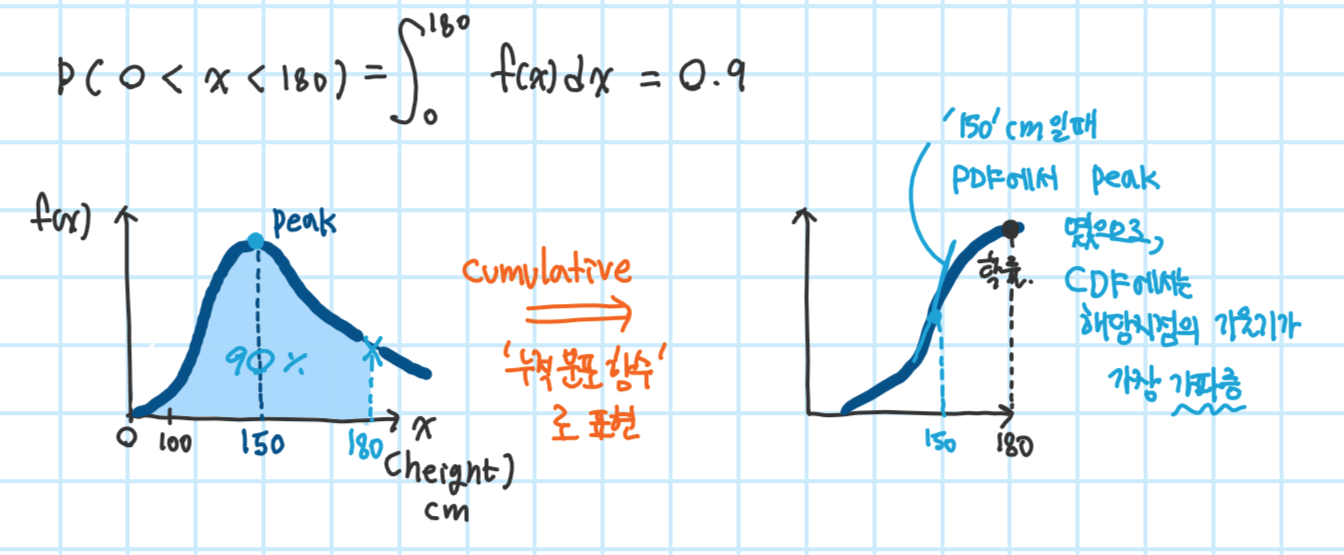
누적 분포 함수(Cumulative distribution function : CDF)

1.3 이항분포, 다항분포, 정규분포
1) 이항분포 : Binomial/Bernoulli distribution
- 이진 확률 변수 X의 분포
- 이항 분포의 확률 질량 함수 (PMF)
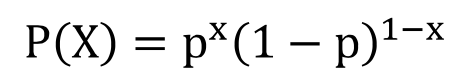
2) 다항분포 : Multinomial/ Categorical distribution
- 이항 분포가 일반화된 것(yes/no -> 1~6)
- 다항 분포의 확률 질량 함수(PMF)

- k : 카테고리의 수
- p_k = P(X=k), for k = 1,2,...,k
- 머신러닝에서 one-hot encoding과 함께 사용됨
3) 가우시안 분포 : Gaussian distribution (정규 분포 Normal distribution)
- 가우시안 분포의 확률 밀도 함수(PDF)
- real world를 approximate 하기 좋아 여러 분야에서 많이 사용되는 분포
- 장점: 평균과 분산만으로 분포를 완전하게 표현 가능
Univariate


- σ와 기울기는 반비례 관계
Multivariate
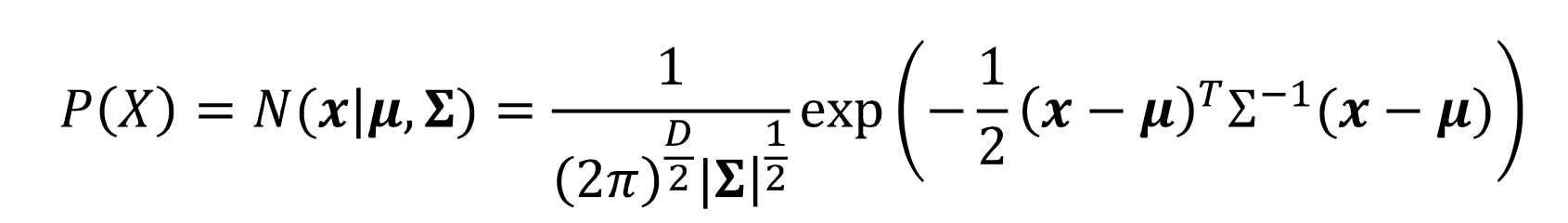

1.4 조건부 확률과 베이즈 정리
1) 조건부 확률 : Conditional probability
- 조건부 확률이란 어떤 사상 A가 일어났다고 가정한 상태에서 B가 일어날 확률을 의미하고 수식은 아래와 같음
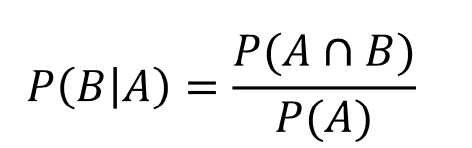
- P(B|A)는 전체 표본 공간을 사건 A로 축소시킴. 또한 조건부 확률에서 다음처럼 정의할 수 있음
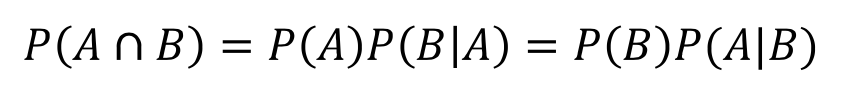
- 자연어 처리에서 P(A)P(B|A)를 사용할 때, A는 B의 확률을 계산하기 위해 주어진 히스토리, 문맥, 지식이라 생각할 수 있음. 주어진 지식 A가 B의 확률을 계산하는데 영향을 미칠 수도, 그렇지 않을 수도 있음. 만약 A가 B의 계산에 영향을 미치지 않을 경우 둘을 독립이라 하며 다음처럼 나타낼 수 있음
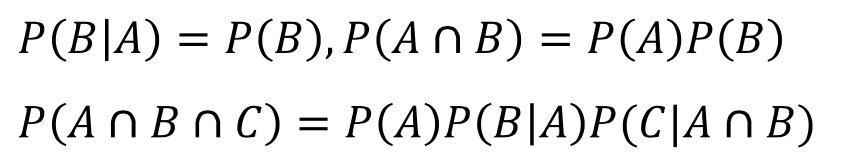
2) 베이즈 정리
- 표본 공간이 B1, ... , Bn의 사건들로 서로 겹치지 않게 분할되어 있을 때 어떤 사건 A를 다음처럼 계산할 수 있음
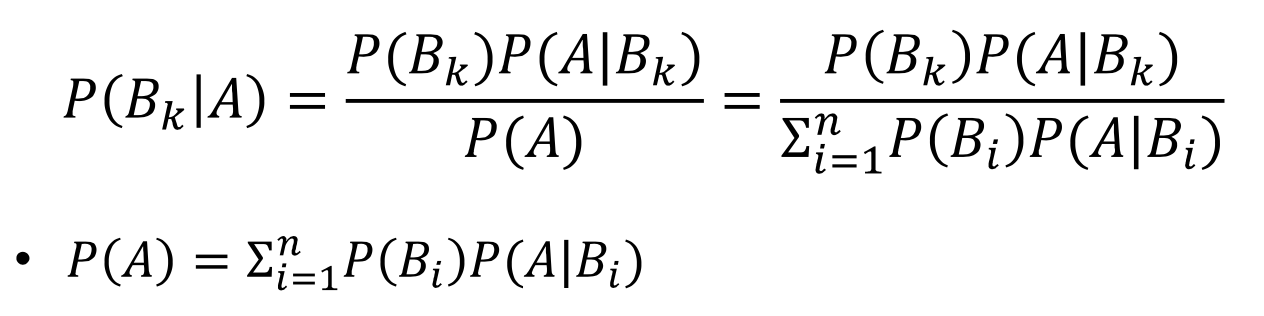
예) 병원 암 진단 검사에서 양성이 나왔을 때, 진짜 암일 확률은?


예) Spam filtering
목적
- 입력으로 email(x)가 들어오면, spam(Y=1)인지 아닌지(Y=0) 구분하는 text classification 알고리즘을 만들자
방법
1) 데이터의 생성(확률) 모델 정의
2) 파라미터를 주어진 데이터를 이용해 학습
3) 새로운 입력 X에 대한 라벨 Y를 역으로 추정(베이즈 규칙 활용)


1.5 기댓값과 분산
기대값 : Expectaion, E(X)
일종의 평균과 같은 역할. 한 개의 주사위를 던지는 사상을 가정하자. 나오는 눈을 확률변수라 할 때 1부터 6까지 모든 면이 동일한 확률로 나온다면 확률변수의 값은 다음처럼 기대할 수 있다

- 만약 모든 면이 동일한 확률로 나오지 않는다면, 어떤 값과 그 값이 나올 확률에 대한 가중 평균이 될 것
- 기댓값은 어떤 정확한 값이 아니라 나오게 될 숫자에 대한 예상임. 확률 변수의 평균이라 생각할 수 있음
- 평균은 X의 확률분포의 중심 위치에 대한 측도로 사용할 수 있음
이산 확률 변수와 연속 확률 변수의 기댓값은 다음처럼 계산할 수 있음

분산 : Variaton, V(X)
- 확률분포에서 확률 변수들이 퍼져 있는 정도이며, 각 값이 평균값에서 얼만큼 떨어져 있는지 보여줌 이를 편차라고 함
표준편차란 분산의 제곱근이며 다음과 같이 나타냄
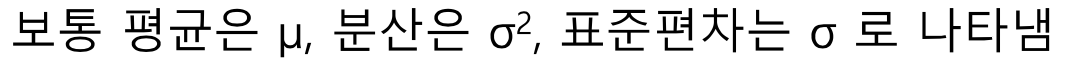
분산은 다음 두 방식으로 나타낼 수 있음
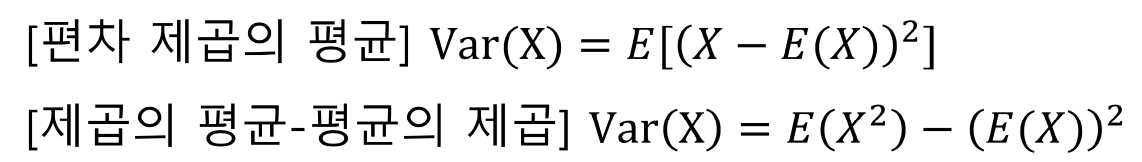
요약

2. 최대 우도 추정과 최대 사후 확률 추정(MLE & MAP)
2.1 최대 우도 추정 : Maximum likelihood estimation(MLE)
동전을 던질 때 앞면이 나올 확률을 θ라 하면, 다음과 같이 확률을 정의할 수 있음
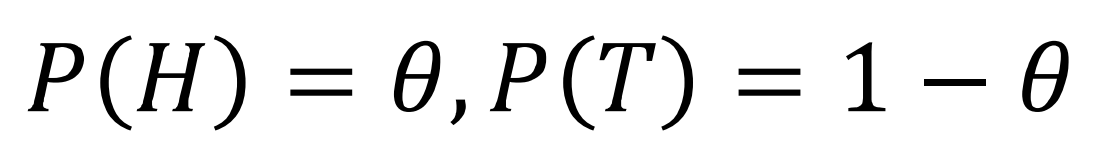
일반화하면 다음과 같음
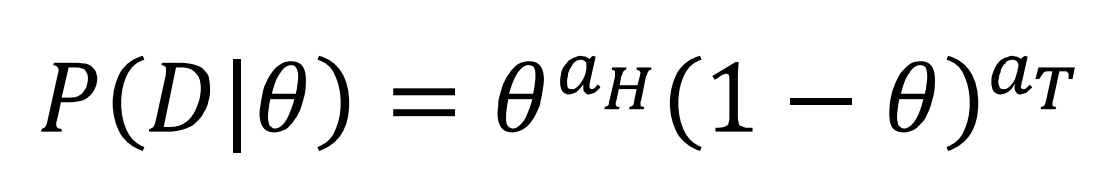
우리의 목적은 θ들 중 최적의 후보를 택하는 것, 다음 같은 수식으로 나타낼 수 있음

- P(D|θ) : θ가 주어졌을 때 D가 나올 확률들의 분포로 즉 θ들의 분포를 의미함
- 주어진 θ에 따라 결과값의 가능성(likelihood)는 달라짐
- θ는 데이터를 가장 잘 설명할 수 있어야 함
- 우리의 관심사는 θ가 어떤 값일 때 P(D|θ)가 최대인지 찾는 것
θ를 찾는 방법은?
함수의 최댓값 또는 최솟값을 구하기 위해서는 그래프의 모양을 알고 미분으로 구할 수 있다.
계산의 편의를 위해 단조증가함수인 로그함수를 취하여 미분하자

MLE의 문제점?
- 5번의 시도만으로 과연 앞면의 확률이 1/5라 단정 지을 수 있는가?
- 즉, 초기 관측 데이터에 대해 쉽게 과대적합(overfitting)됨
MLE의 가정
- 무한대의 관측 데이터가 주어질 경우, MLE로 예측된 파라미터 θ는 실제 파라미터로 수렴
- 하지만, 제한된 수량의 관측 데이터만 주어진다면 이를 보장할 수 없음
2.2 사후 확률 추정 : Maximum a Posteriori(MAP)
베이즈 정리를 이용한 θ 업데이트
경험적으로 확률이 반반인 동전이 많았음, 파라미터 θ에 대해 우리 경험을 바탕으로 한 확률적인 가정을 더하자

아래의 식을 사용해서 θ의 분포를 구하는게 목적

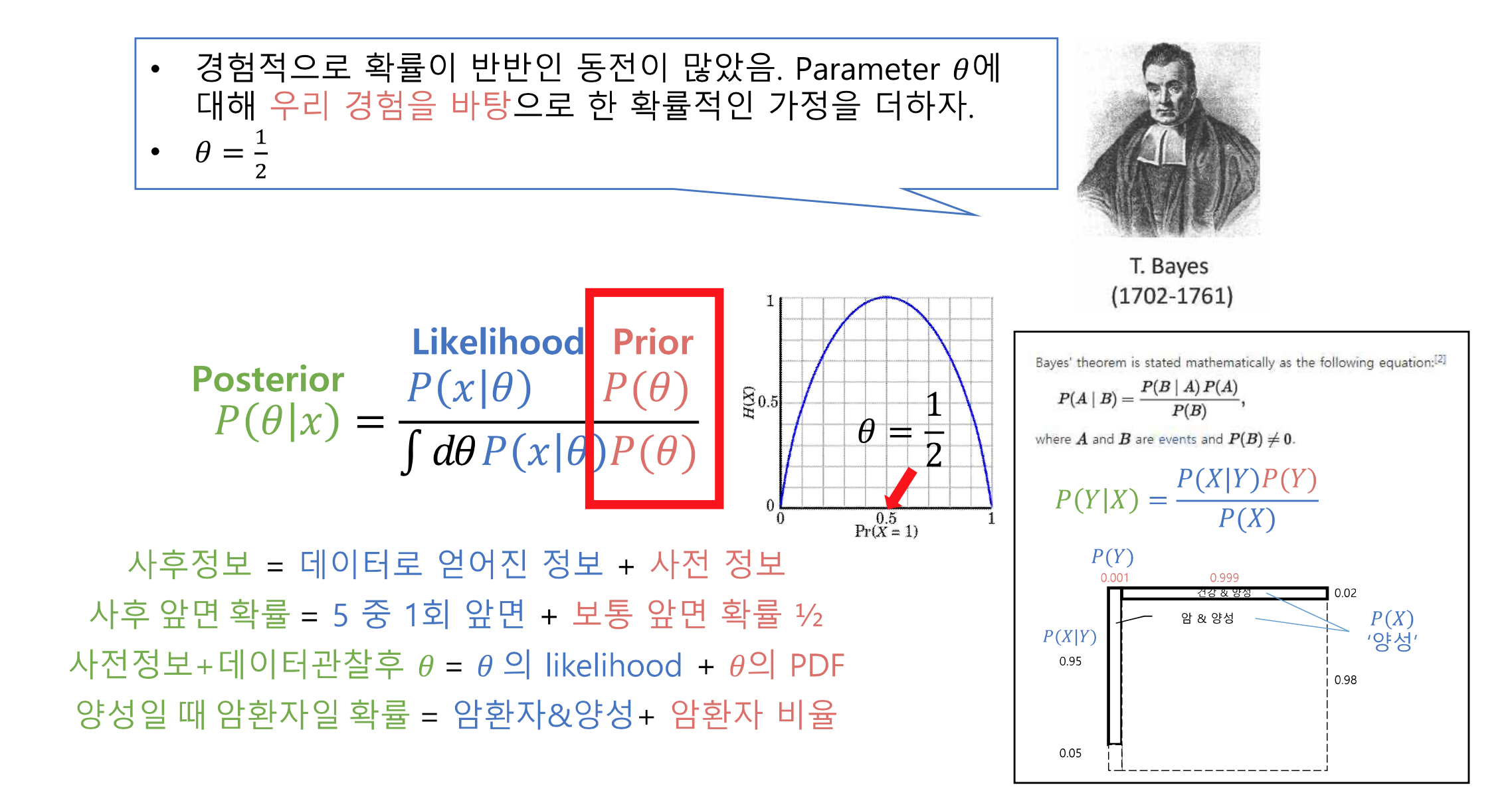
요약
1. 관측된 데이터를 가장 잘 설명하는 파라미터 θ(분포)를 찾기 위해 MLE 사용
2. Bayesian approach : 파라미터에 확률 분포를 추가적으로 가정한 후 posterior를 통해 최적의 파라미터 θ를 추정(MAP)
3. posterior : likelihood를 통해 데이터를 관측하고 정보가 업데이트 된 prior(이 후 다른 추정의 prior로 재활용 가능)

3. 정보이론과 엔트로피(Information theory & entropy)
3.1 정보량
1) 정보 이론
- Claude Shannon이 1984년 처음 제시한 이론
- 임의의 정보에 대해 데이터 압축률과 전송률을 최대화할 수 있는 수학적 모델을 제시하고자 함
2) 정보량
- 정보량을 다음과 같이 수식으로 나타낼 수 있음
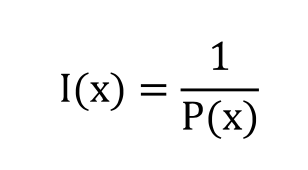
3.2 엔트로피
1) 엔트로피
- 확률분포에서 일어날 수 있는 모든 사건들의 정보량의 기댓값으로 P(X)의 불확실 정도를 평가
- 즉, 어떤 정보의 불확실성이 높은지 낮은지 평가하는 지표
- 엔트로피가 높을 수록 불확실성이 높음
2) 정보량과 엔트로피의 예
- 카드 맞추기
- 동전 던주기
- 공 맞추기
3) 크로스 엔트로피는?

3.3 KL-Divegence, Preplexity
KL-divergence

- 결과값이 낮을 수록 두 분포가 일치하는 정도가 높다고 생각하면 됨
- 딥러닝을 이용한 자연어처리, 강화학습에서 모델 학습 시, 어떤 두 분포를 일치하도록 해야할 때 학습지표 등으로 사용
- 기계학습에서 loss function과 유사

