03 Analytic Geometry

(해당 강의노트는 Marc Peter Deisenroth, A. Aldo Faisal and Cheng Soon Ong, 『Mathematics for Machine Learning』을 기반으로 작성하였습니다)
03 Analytic Geometry: 해석 기하학
목차
- Norm & inner product
- Orthogonality
- Orthogonal projections
- Rotations
1. Norm & inner product
1.1 Norm
- Definition: 벡터 공간 위의 norm은 실수로 가는 mapping function임

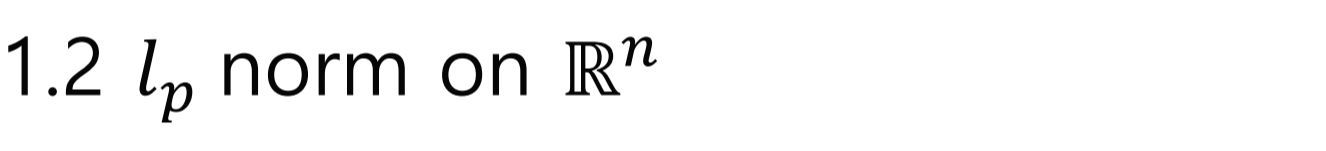


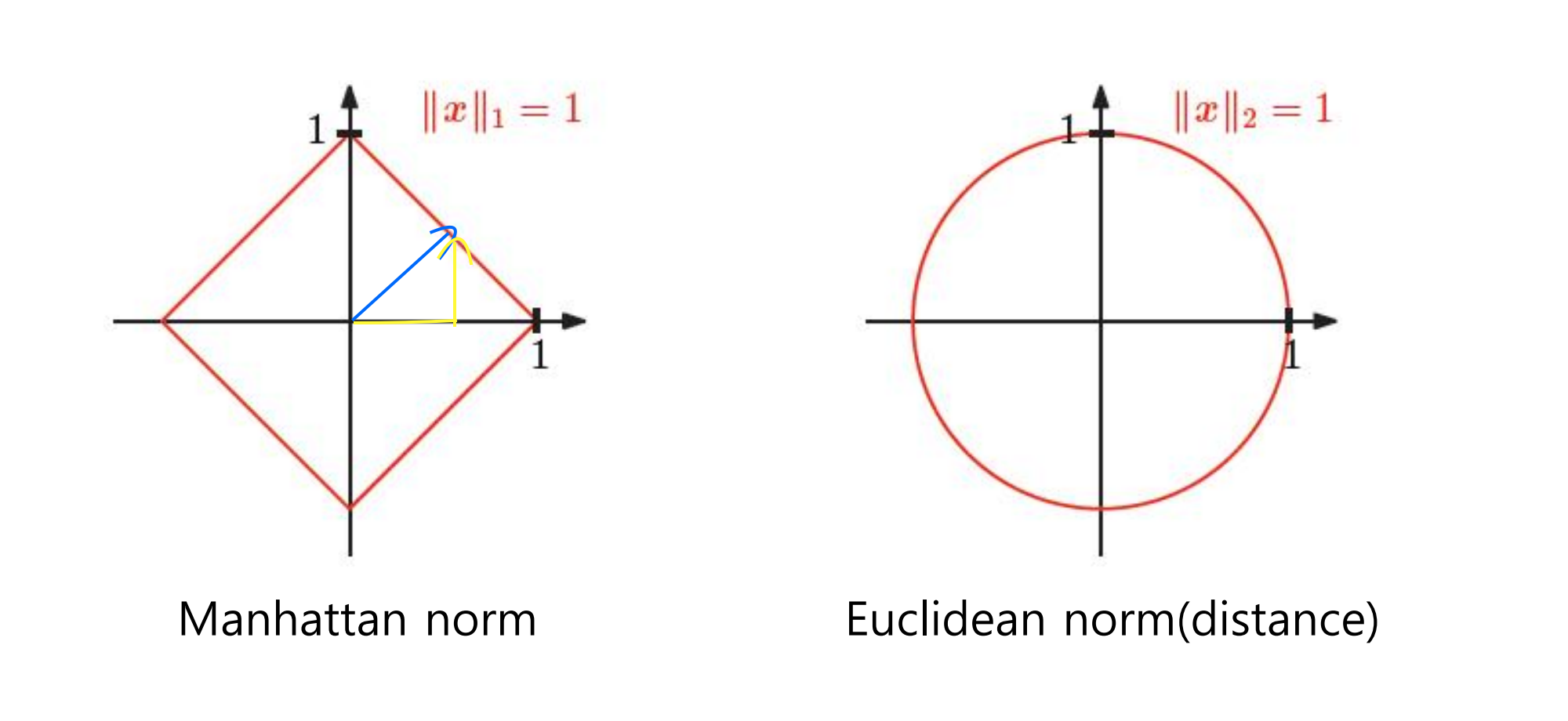
1. Manhattan norm
- 모든 벡터의 manhattaon norm이 1인 end point를 가진 그래프
- 파란 벡터의 manhattan norm은? : 노란 벡터 두개를 더한 값이 항상 1임
- 벡터의 성분을 모두 더한 길이
2. Euclidean norm(distance)
- 원점으로부터 거리가 1인 벡터들의 end point를 모아놓은 것
- 벡터의 크기 공식과 동일
실습: 파이썬에서 Manhattan norm과 Euclidean norm(distance)그리기
1. import library
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (10,10) # size control of plot2. Euclidean Norm: $$l_2 norm$$
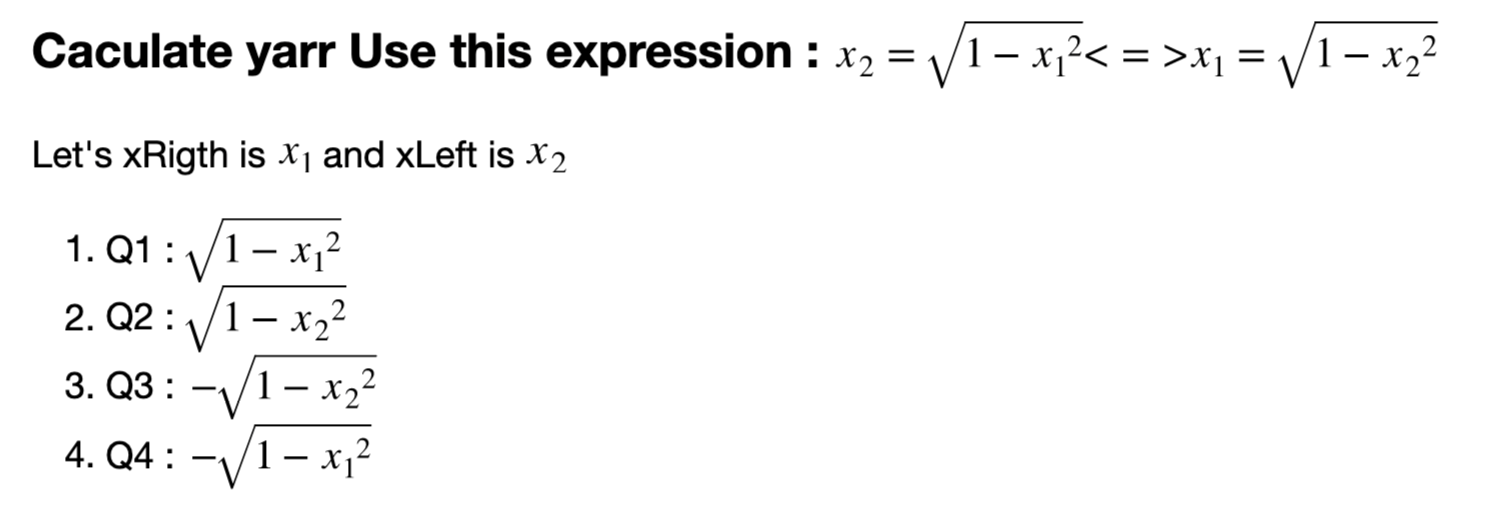
# 1. draw 12norm
xRight = np.linspace(0,1,50) # 0 to 1
xLeft = np.linspace(-1,0,50) # -1 to 0
# declare array
xarr = [xRight, xLeft, xLeft, xRight] # x coordinate for Q1, Q2, Q3, Q4
xarr = np.array(xarr) # list -> array [4,50]
xarr = xarr.reshape(-1) # reshape to one line [1,200]
yarr = [np.sqrt(1-xRight**2), np.sqrt(1-xLeft**2), -np.sqrt(1-xLeft**2),-np.sqrt(1-xRight**2)]
yarr = np.array(yarr).reshape(-1) # reshape to one line
plt.scatter(xarr, yarr, s = .5, color ='r')
plt.title('Euclidean Norm(L2, red)')
plt.show()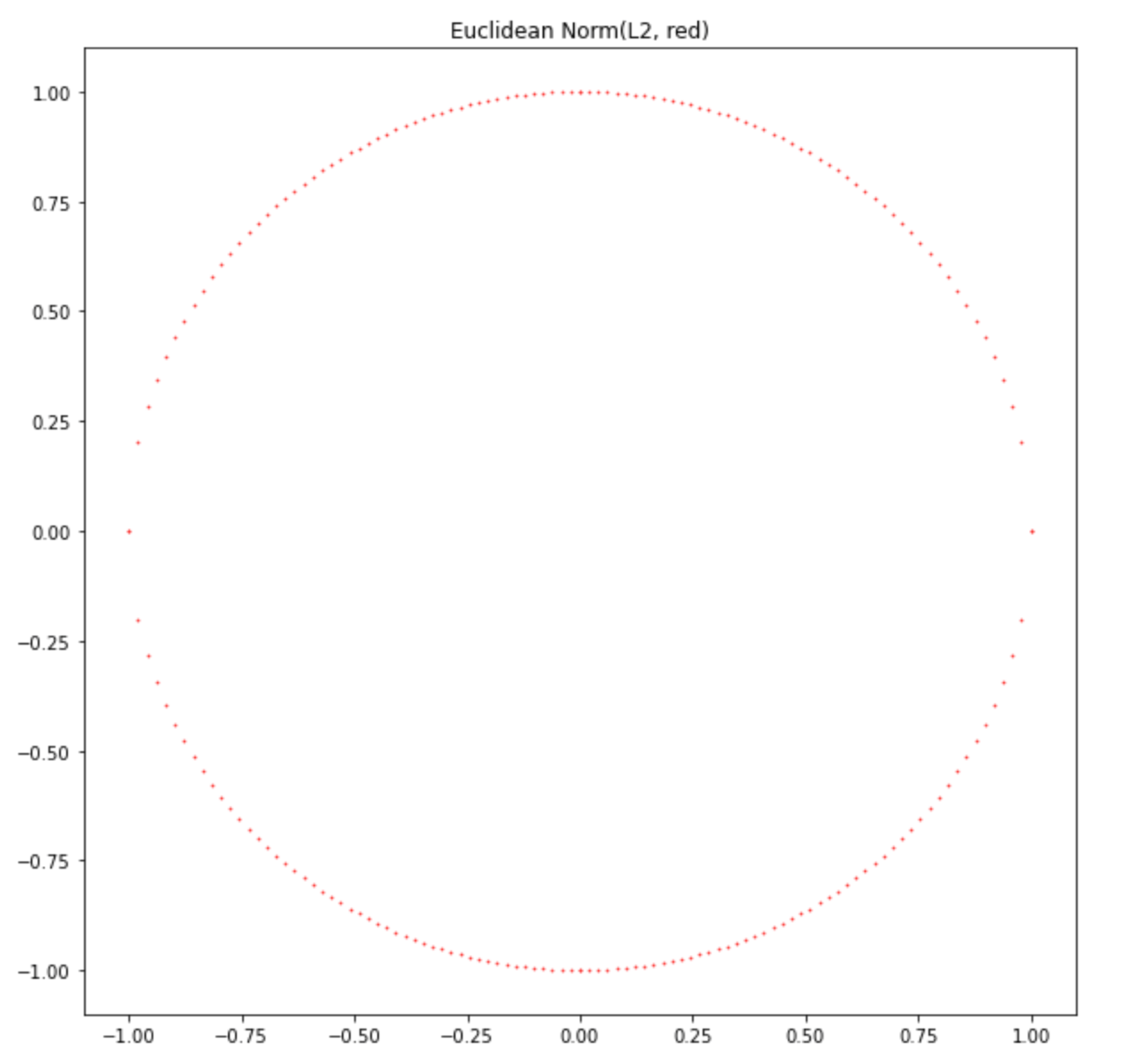
3. Manhattan Norm: $$l_1 norm$$
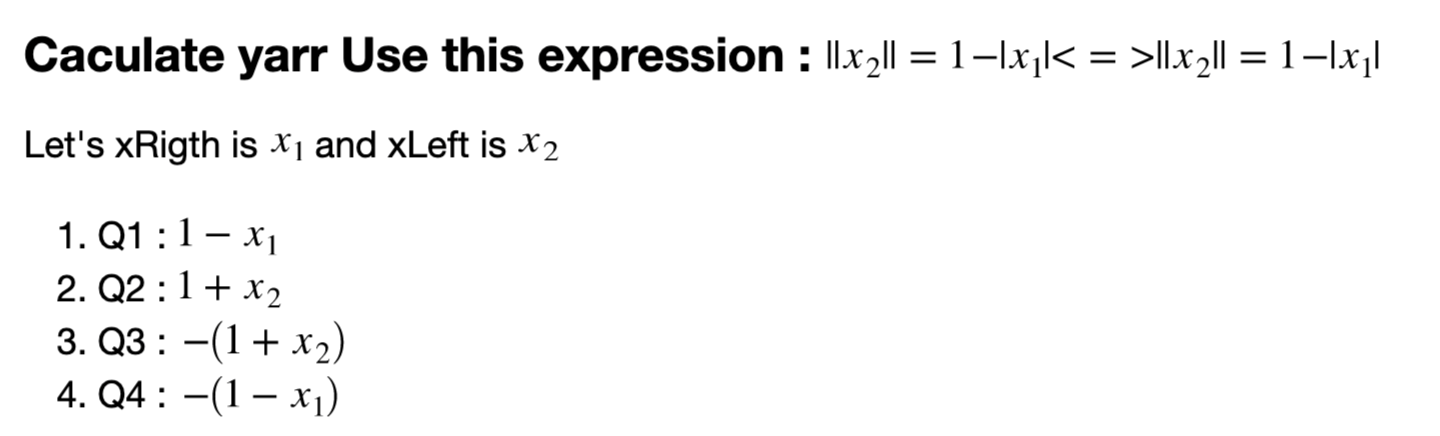
# 1. draw 11 norm
xarr = [xRight, xLeft, xLeft, xRight] # x coordinate for Q1, Q2, Q3, Q4
xarr = np.array(xarr) # list -> array [4,50]
xarr = xarr.reshape(-1) # reshape to one line [1,200]
yarr = [1-xRight,1+xLeft, -(1+xLeft),-(1-xRight)]
yarr = np.array(yarr).reshape(-1) # reshape to one line
plt.scatter(xarr, yarr, s = .5, color ='b')
plt.title('Manhattan Norm(L1, blue)')
plt.show()

1.3 Inner Product (+ Machine Learning)
- 두 벡터의 유사도 측정시 이용, 유사도와 비례 관계
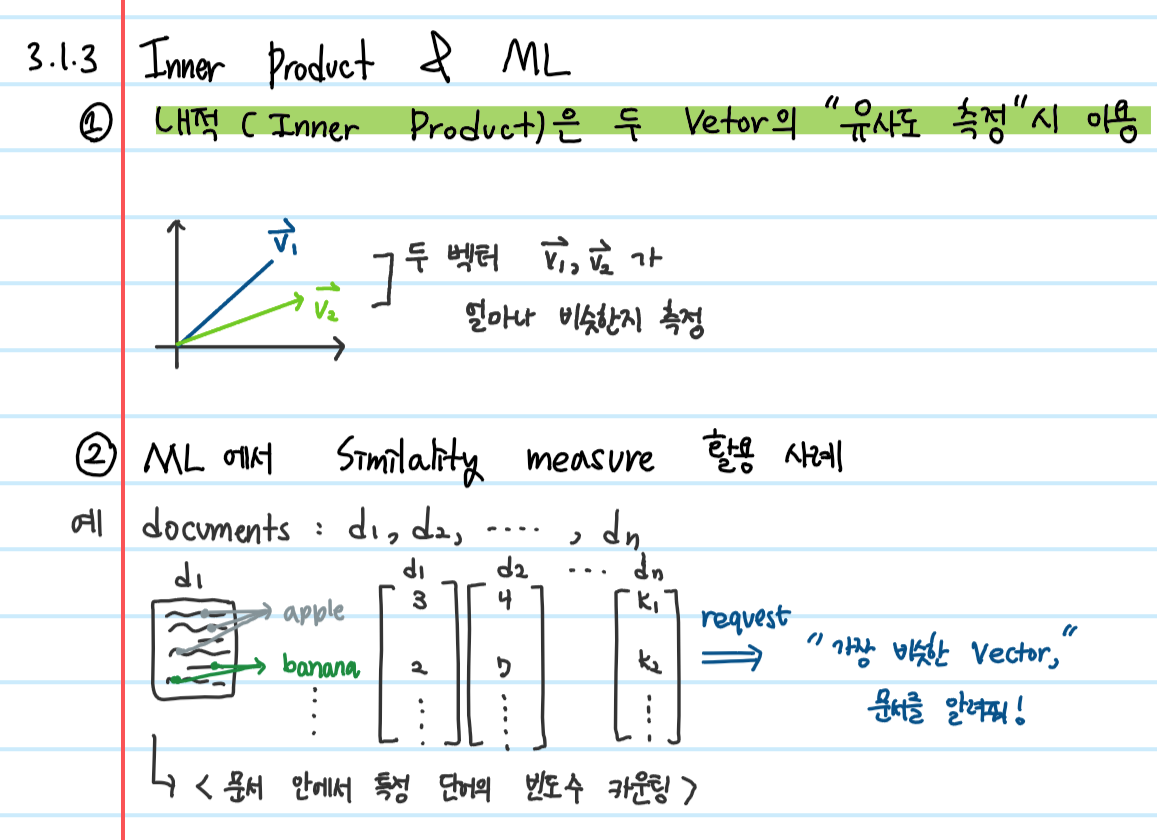
- definition
$$<x,y> = x^Ty$$
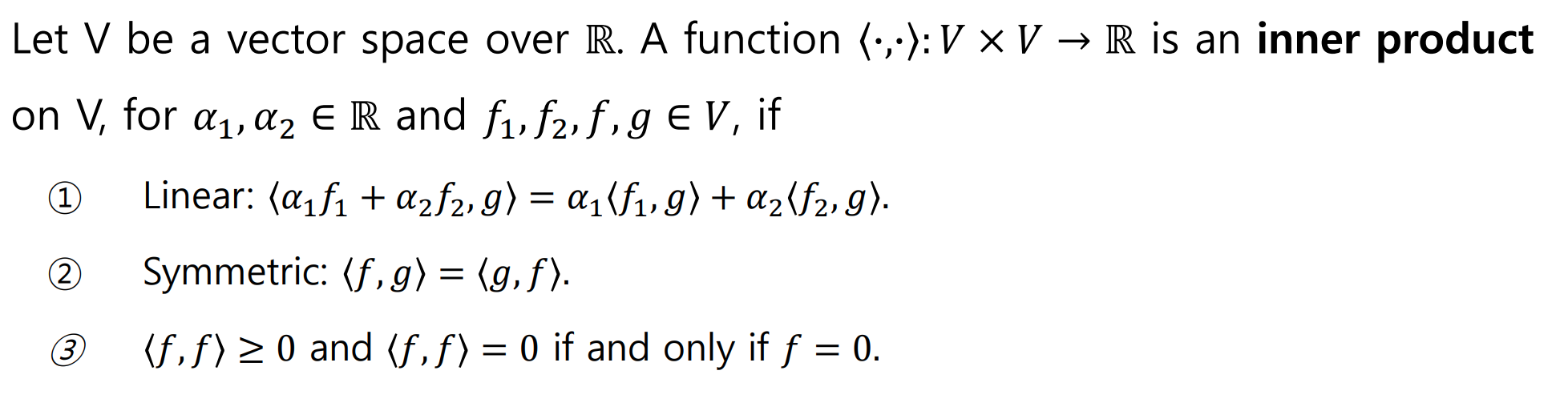

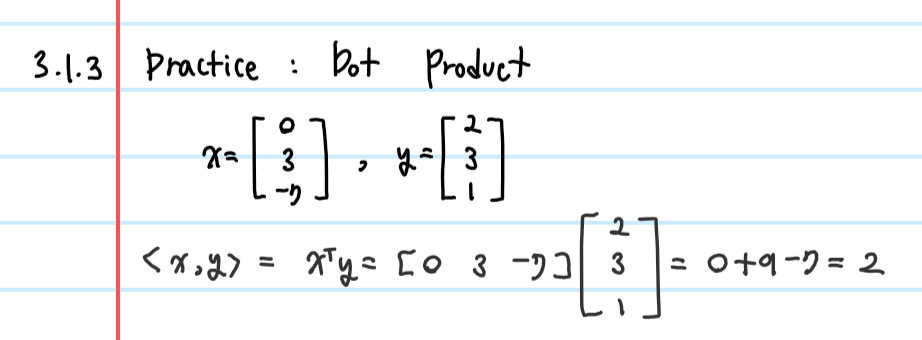
1.4 Distance
1. Inner product와 같이 두 벡터의 유사도 측정 시 사용됨
- 단, Inner product와 유사도는 비례관계, Distance와 유사도는 반비례 관계임
2. Distance = "두 벡터의 차"의 norm임. Distance 자체는 norm이 아니다!
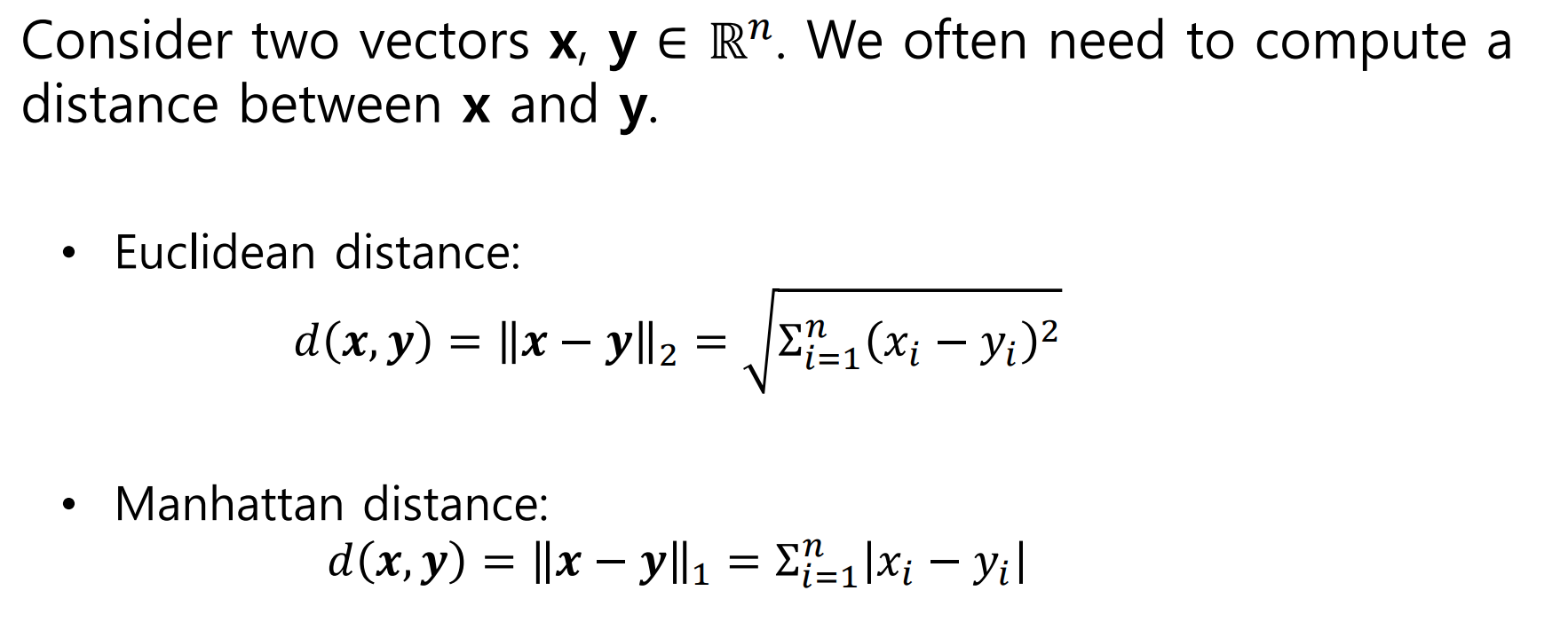
+ week6 Quiz2
Q: 다음 두 벡터의 거리의 제곱을 구하시오(특별한 설명이 없을 경우 Euclidean distance를 의미)
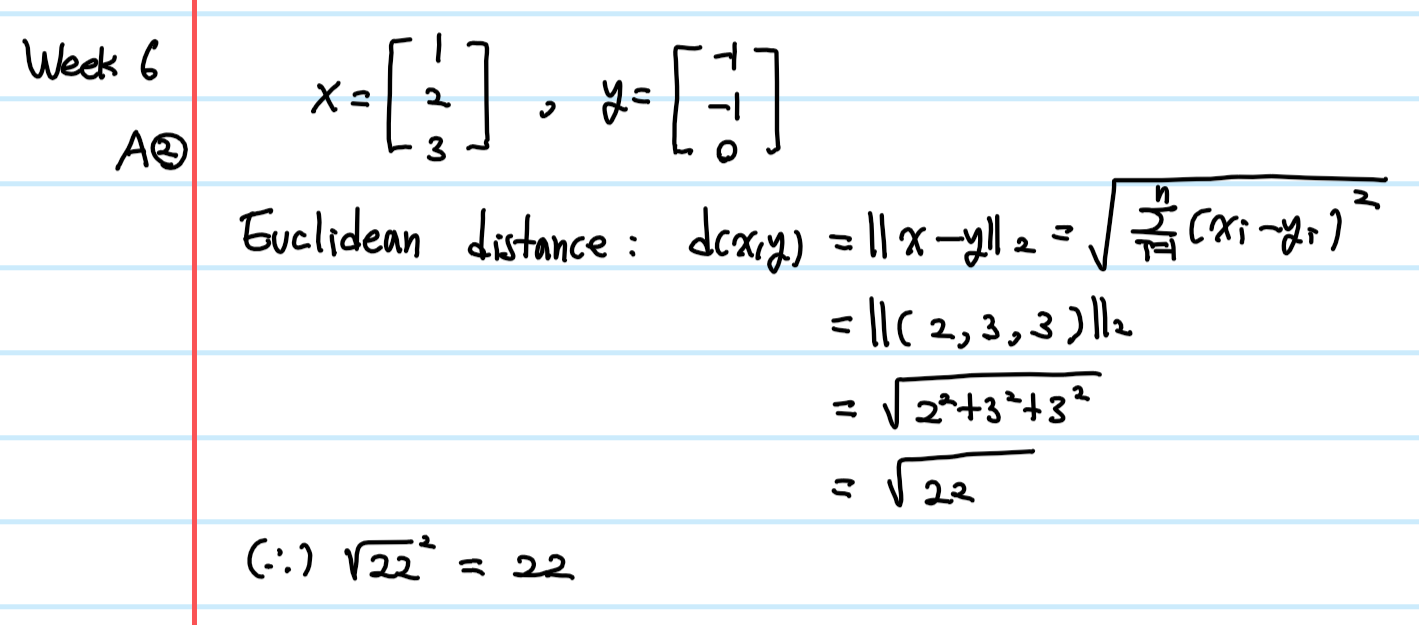
1.5 Angles between Two Vectors
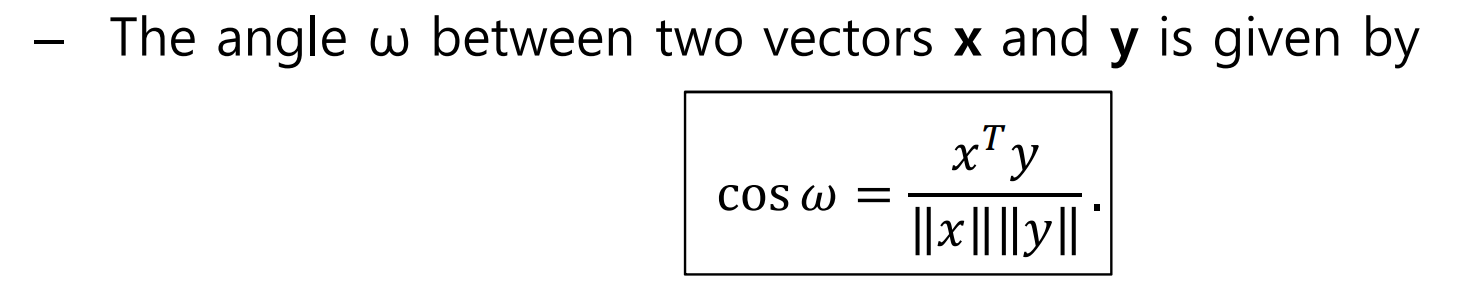
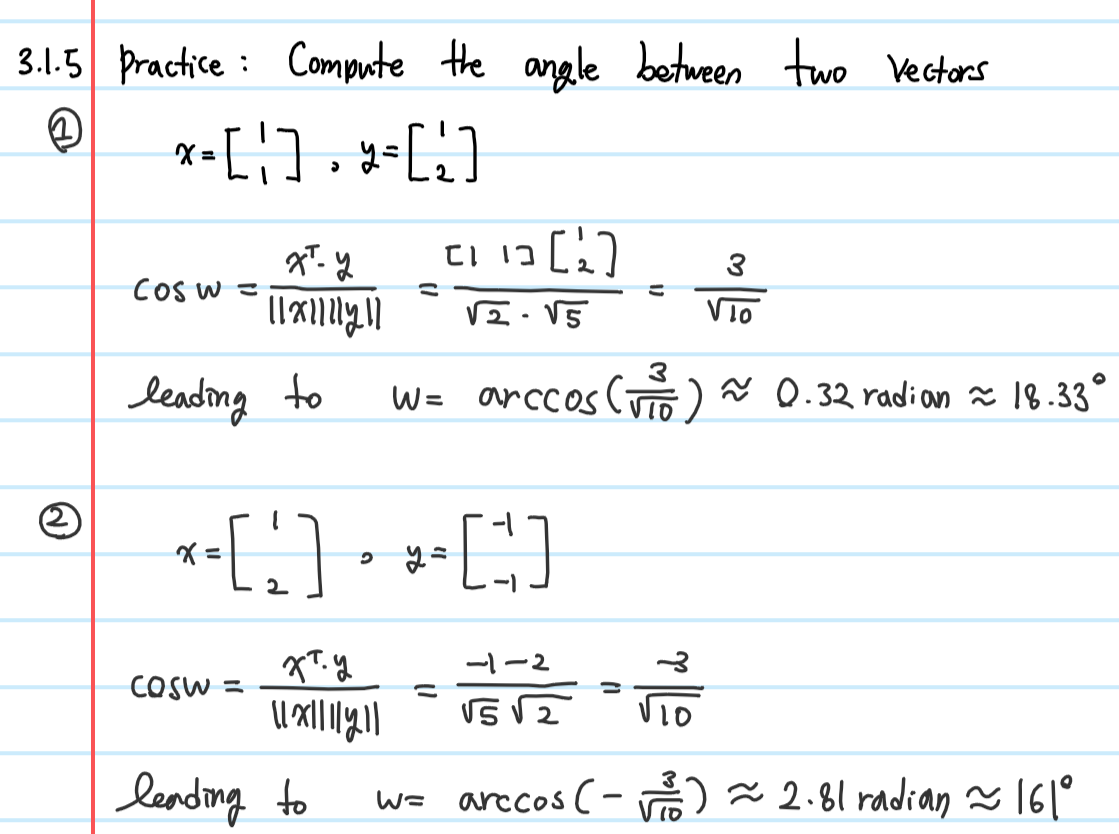
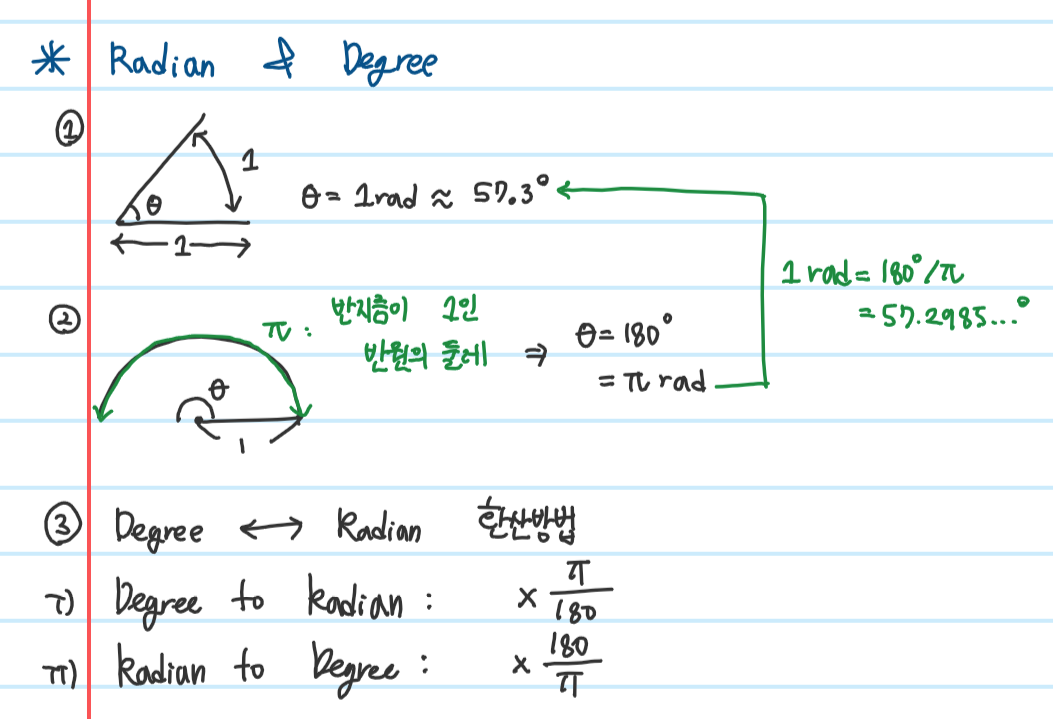
+ week6 Quiz3
Q: 다음 두 벡터간의 각도를 구하시오
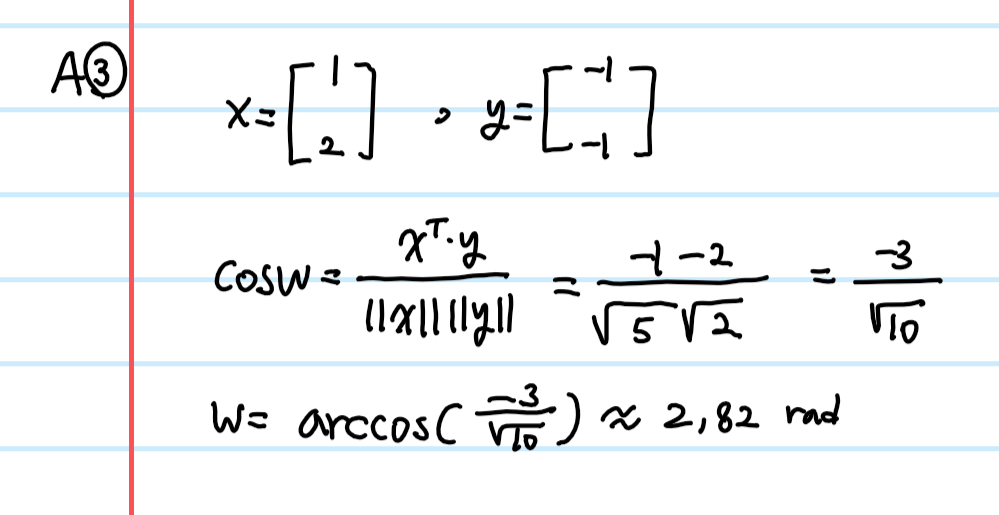
2. Orthogonality
2.1 Orthogonality
- Orthogonality Definition : <x,y> = 0일 경우 x,y는 서로 수직관계이다
이 때, 만약 x,y의 크기가 1이라면 이 두 벡터는 orthonormal하다고 한다.

- 직교행렬이면서 정방행렬인 경우의 가장 대표적인 예는 단위행렬
- Orthogonal matrix definition
: column들이 모두 orthonormal한 경우만 정방향 매트릭스 A가 othogonal matrix이다.
$$AA^T = A^TA = I$$
위의 식을 만족할 경우 아래의 식 역시 만족한다
$$A^(-1) = A^T$$
+ 정방향 매트릭스 A가 orthonormal할 경우 A의 inverse matrix를 구하기 쉬움
$$Ax = b -> x = A^(-1)b -> X = A^Tb$$
2.2 Orthogonal transformation


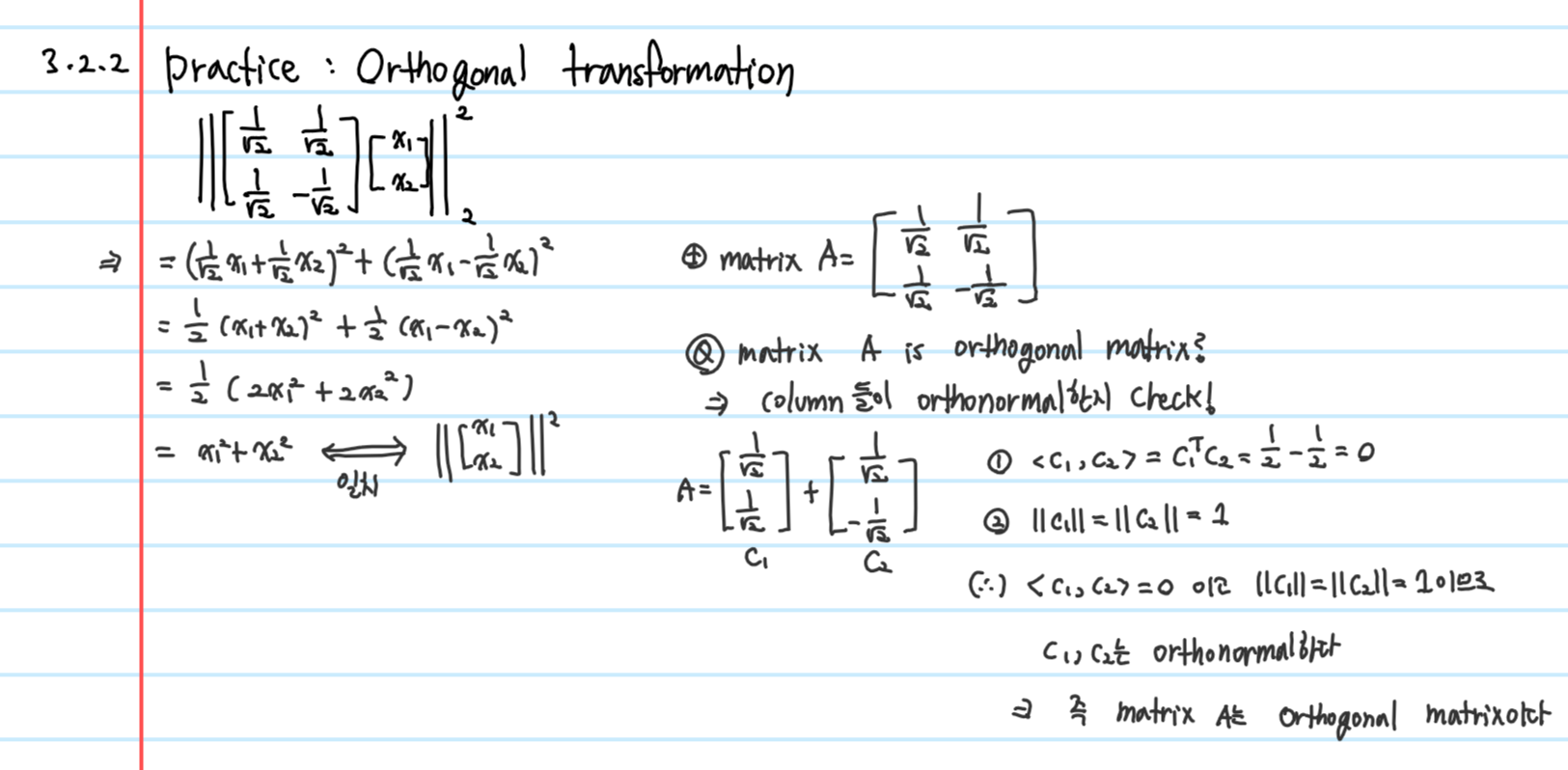
2.3 Linear Orthogonal transform
- Ax can be rewritten as

- basis vector $$a_i$$
- 수학 계산 혹은 엔지니어링에서 basis vector는 주어진다.
- Linear transform은 주어진 시그널 혹은 데이터 b를 계산하는 것과 관련 있음
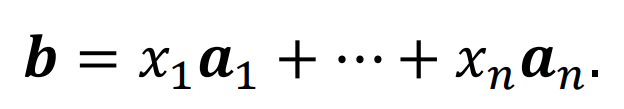
- Orthogonal 한 경우 x는 아래의 식으로 쉽게 계산 가능
$$x = A^Tb$$
- 머신러닝에서는 훈련 세트에서 basis vectors을 어떻게 훈련하는지를 배움(dictionary learning)
- 디지털 신호처리, 컴퓨터 비전에서는 a1,...,an 특정 basis vector를 사용하는 Fourier Transform이 있음
- 수학이나 엔지니어링 분야에서 Linear transform 사용 방법은 basis vector가 주어지면 데이터 b에 대한 coefficient들을 계산하나 기계학습에서는 basis vector들을 미리 정의하지 않고, 학습한다는 것이 큰 차이다.
2.4 Eigenface
: Face recognition
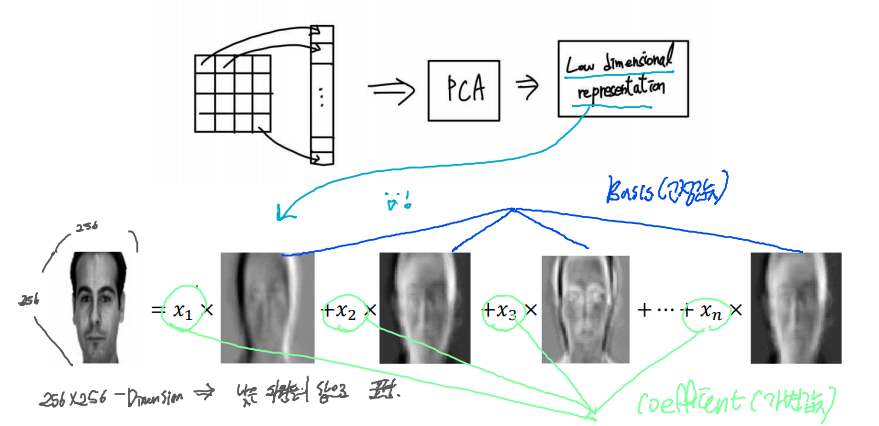
2.5 Gram-Schmidt orthogonalization
n차원 벡터 공간 V의 임의의 basis가 주어졌을 때, V의 orthogonal basis(u_1, ... , u_n)를 반복적으로 계산하는 방법
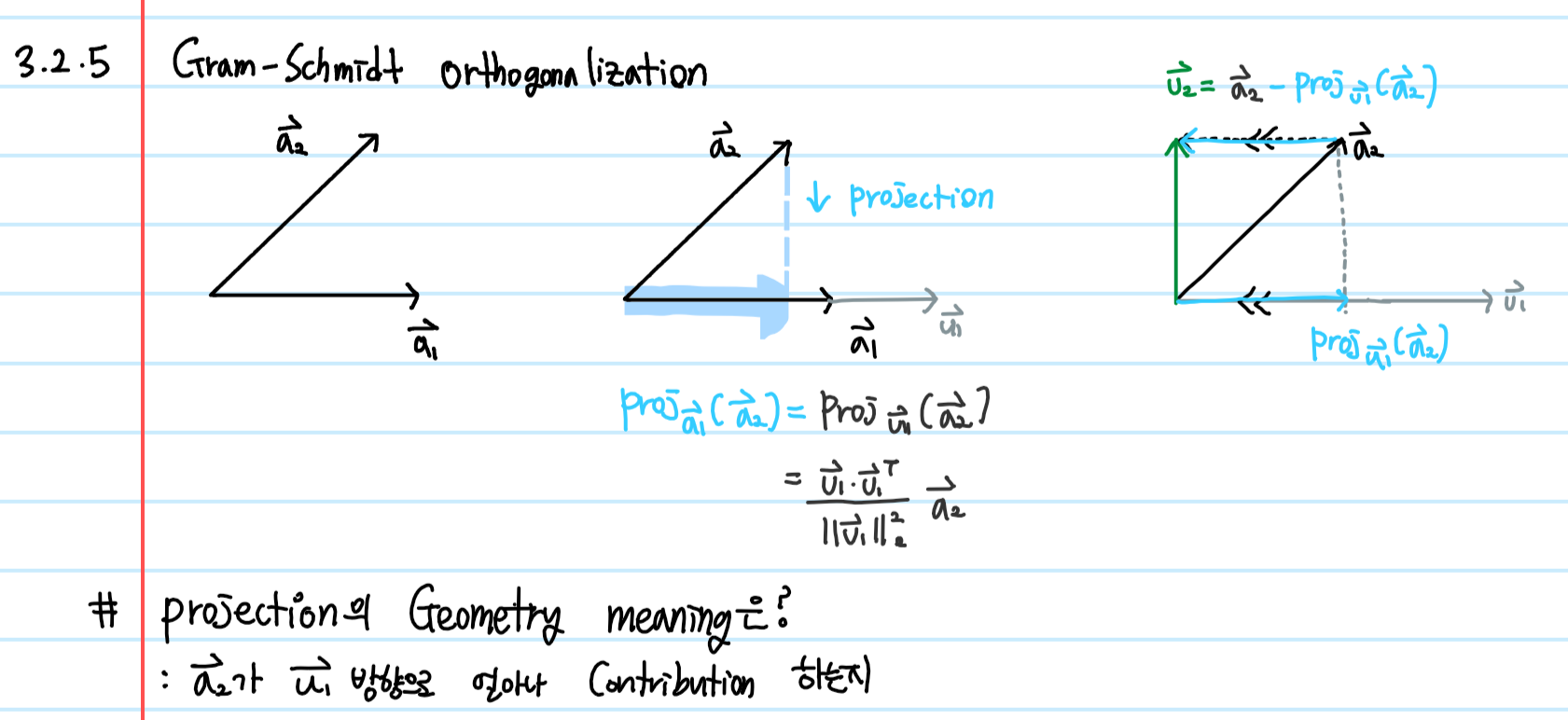
+ week7 Quiz1
Q: 벡터 s를 벡터 r에 projection시킨 벡터 Proj_r(s)를 계산하시오
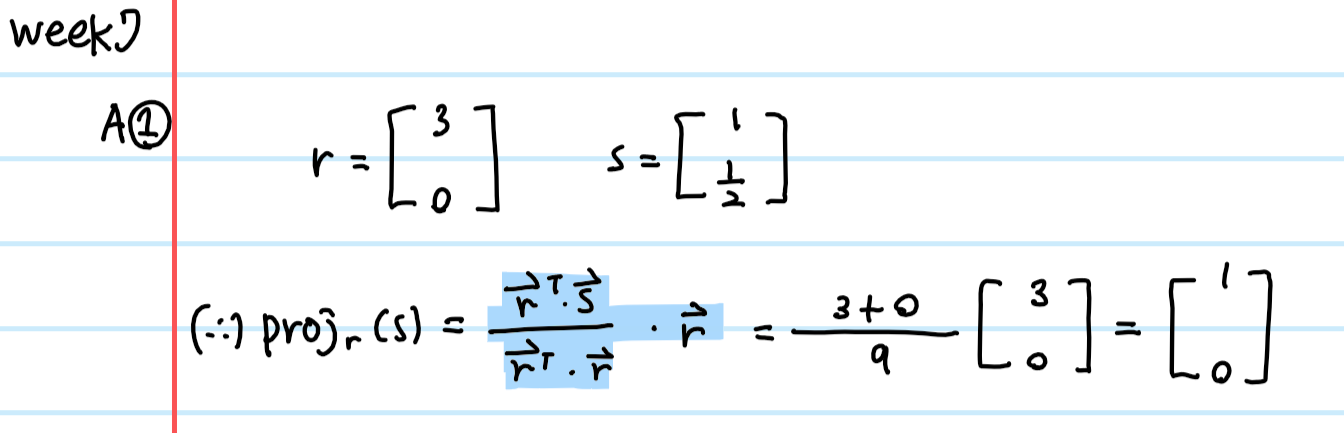
(아래 내용은 알아두고만 있길..일단은 pass)

3. Orthogonal Projections
3.1 Orthogonal Projections
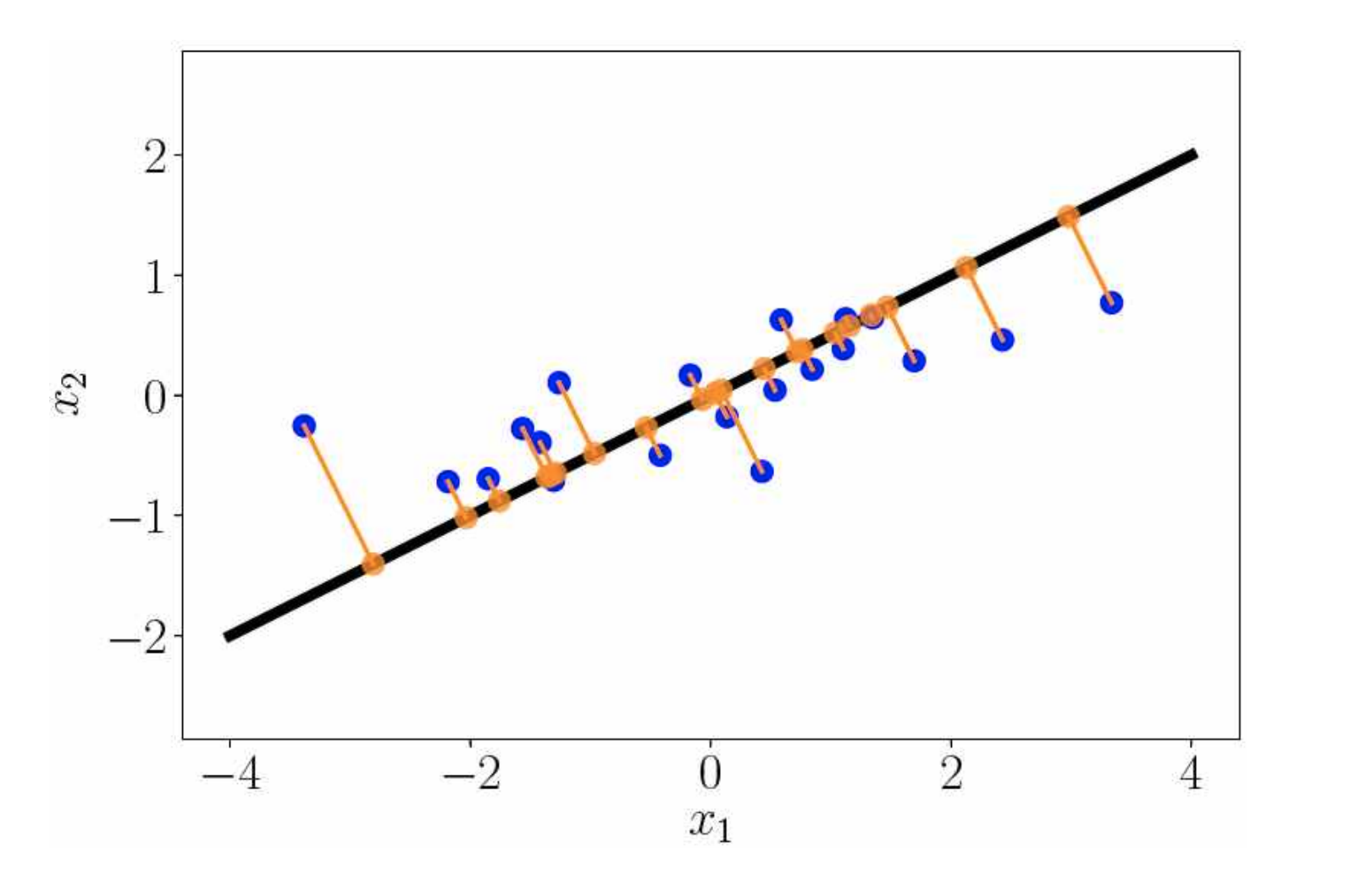
- PCA(Principal Component Analysis) 주성분 분석
1. 고차원 데이터를 저차원 데이터로 축소하는 low-dimensional embedding 문제로 볼 수 있음
2. 주황색 원은 파란 원을 직선 위에 orthogonal projection 했을 때 위치를 나타냄
3. 파란 원은 2차원 공간 상의 데이터를 의미
4. 저차원 데이터로 축소했을 때 장점 중 하나는 데이터를 복잡한 공간이 아닌, 단순한 공간에서 설명할 수 있다는 것
5. PCA를 설명하기 위해서는 파란 원이 x2에 평행하도록 직선에 othogonal projection 되어야 함
- Low-dimensional embedding
: 차원 축소를 위한 mean squared error sense에서 최적의 optimal linear orthogonal transformation을 결정지음
- 목적
: 고차원에서 저차원으로 데이터를 축소하는 과정에서 일어나는 원본 정보의 손실을 최소화하는 것
- 선형회귀에서는 데이터(점)와 직선이 x축의 수직으로 근사시키나 orthogonal projection의 경우 점과 직선이 직교하게 근사시킴
3.2 Hyperplane & Curved manifold
- hyperplane
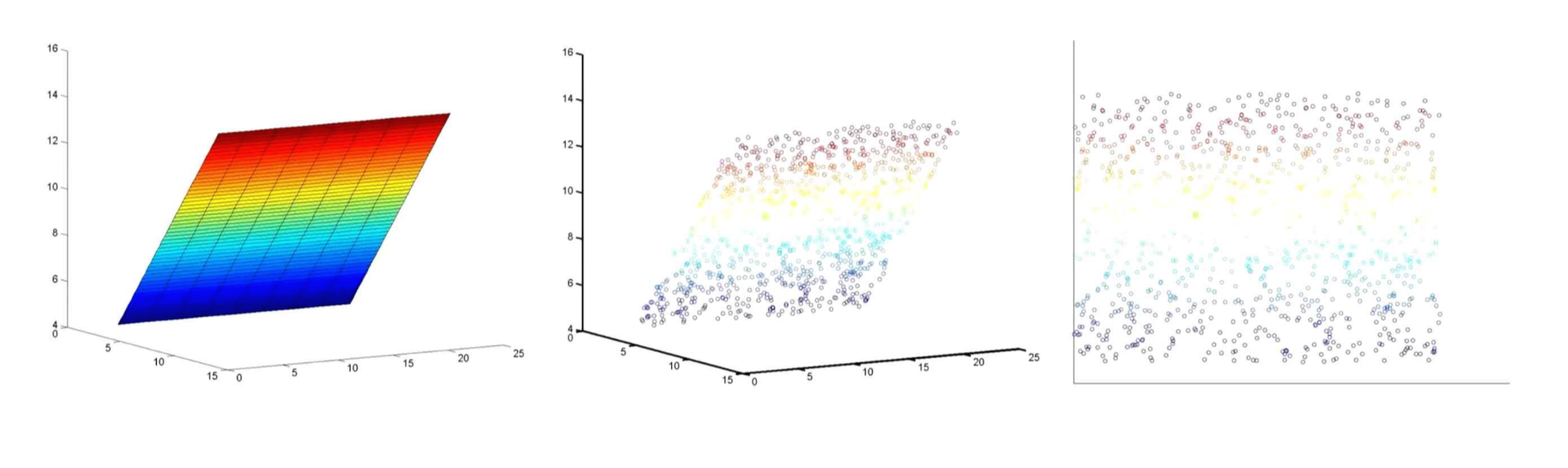
- Curved manifold : unfolding 과정을 거쳐야 함, 대학원 수준의 지식 요구
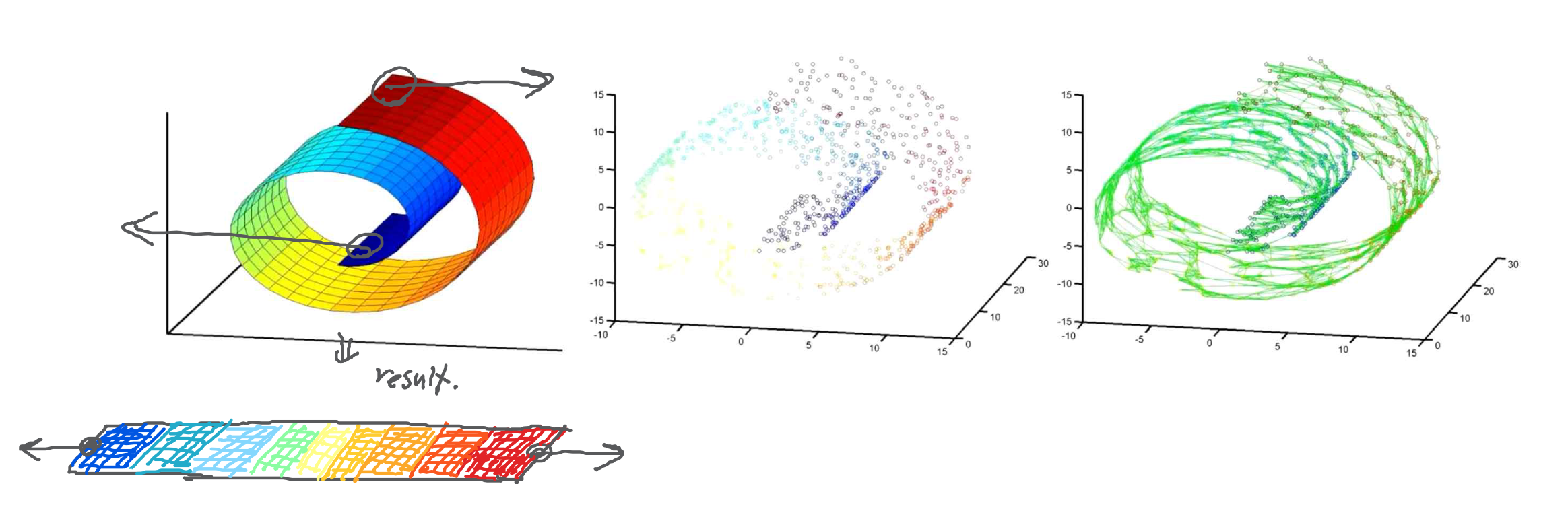
3.3 Projections & Machine Learning
1. ML을 위한 수학에서 우리는 subspace로의 projection 자체를 배운다
2. 머신러닝에서 우리는 종종 데이터로부터 subspace를 학습할 필요가 있다.
: projection과 같은 적절한 저차원 임베딩
3. curved manifold의 예시
: 두 골프 사진의 중간지점을 찾는 것이 목표
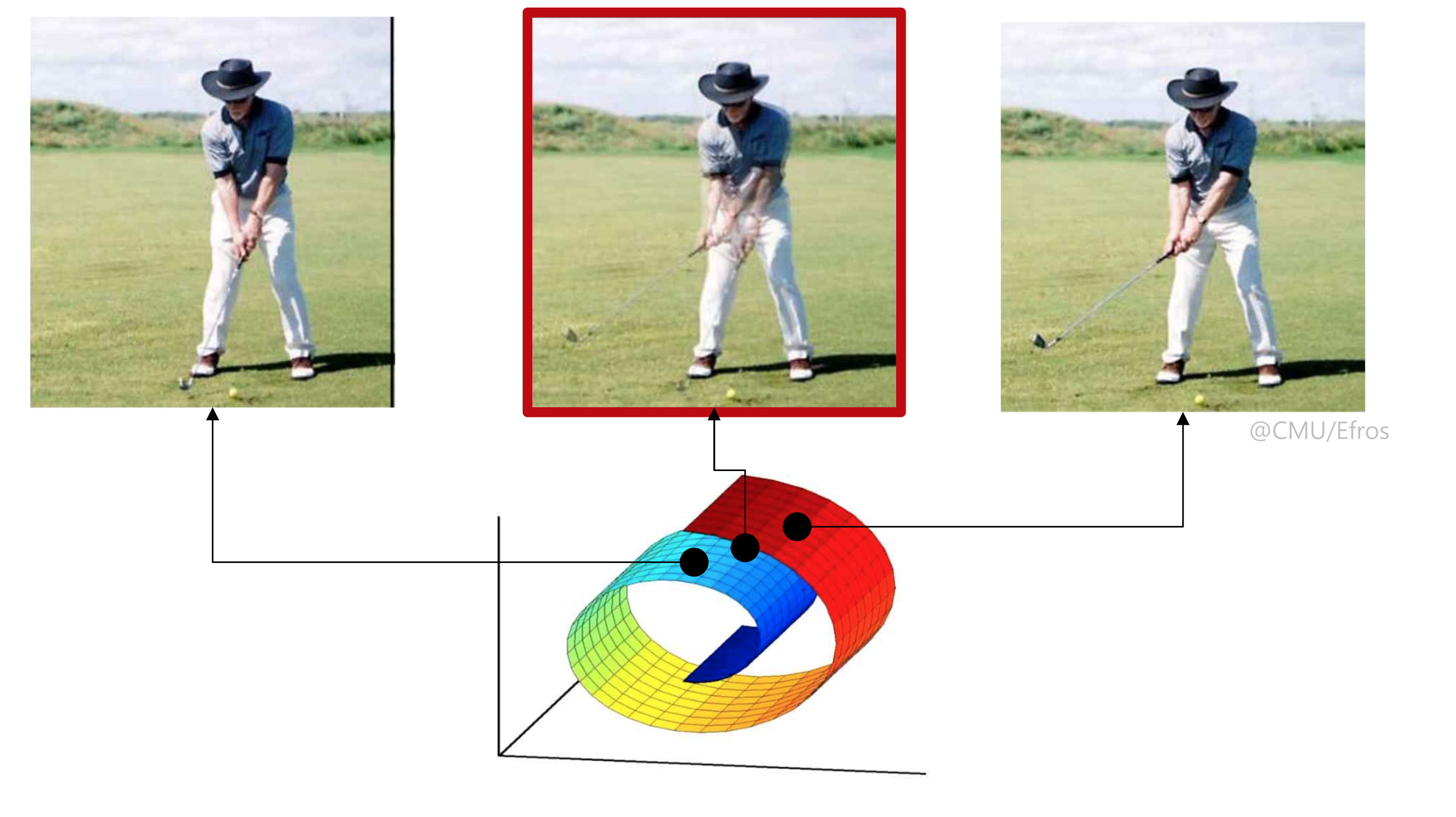

3.4 Projection onto a line
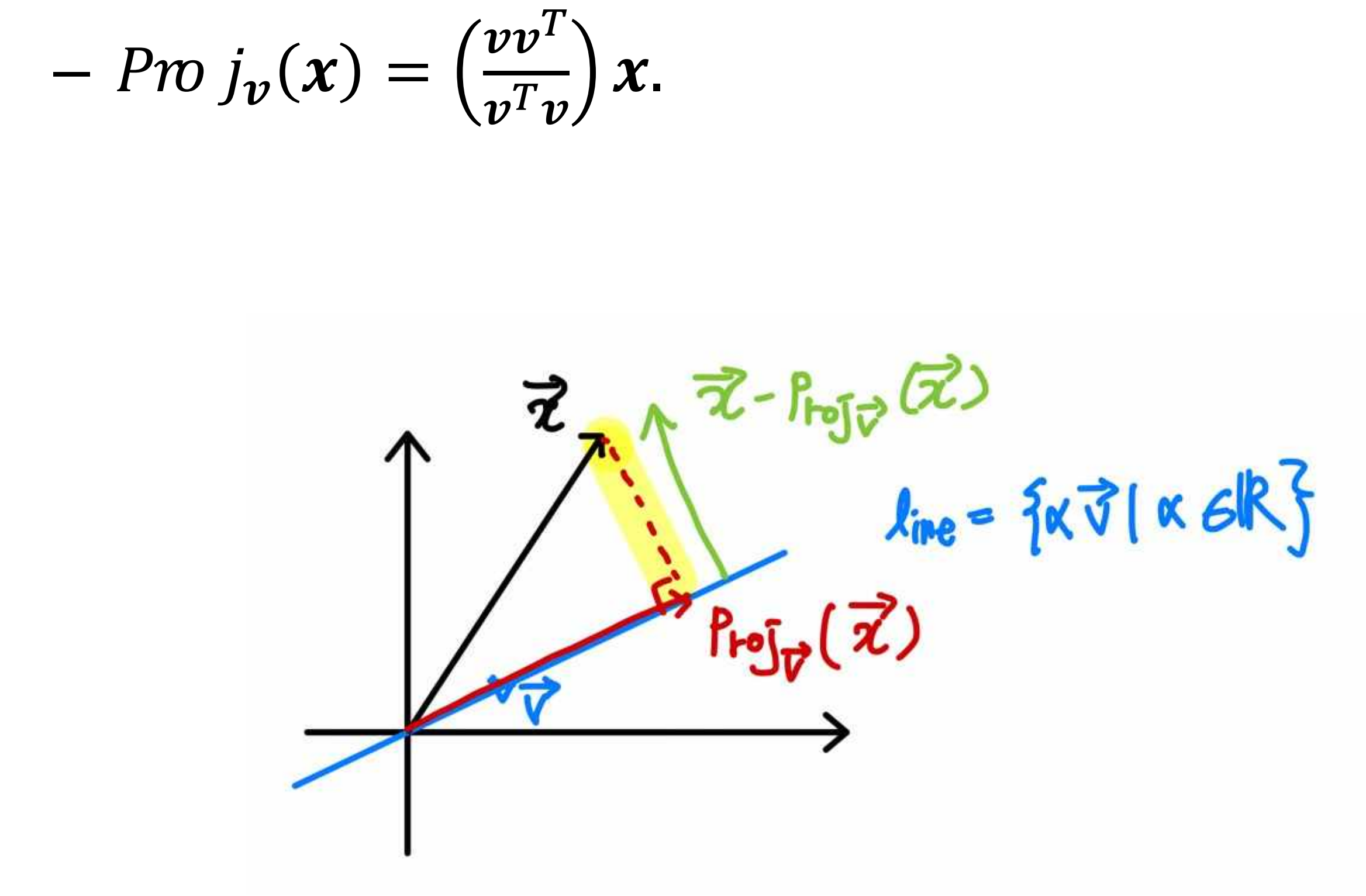

3.5 Projection in a Higher-Dimension
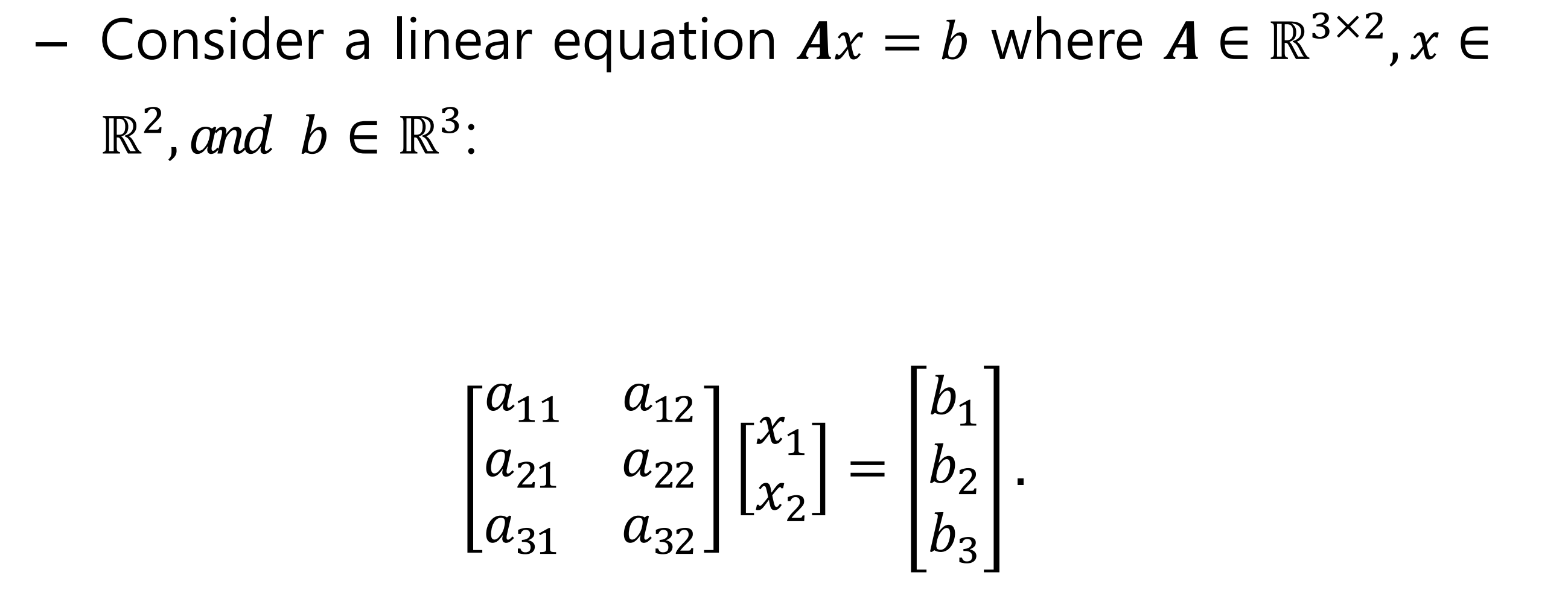
- 실전에서 vector b는 A의 column space와 같지 않을 확률이 높음
- 문제 해결을 위해서는, A의 column space안의 vector p로 vector b를 project해야 한다. 또한 아래의 식을 해결해야 함
$$Ax = p$$
- 해당 식은 머신러닝에서 least squares solution로 볼 수 있음
: 머신러닝에서는 대부분 식이 미지수 보다 많은 skinny matrix를 볼 수 있는데 이는 해를 구할 수 없는 형태로 approximate하게 구함
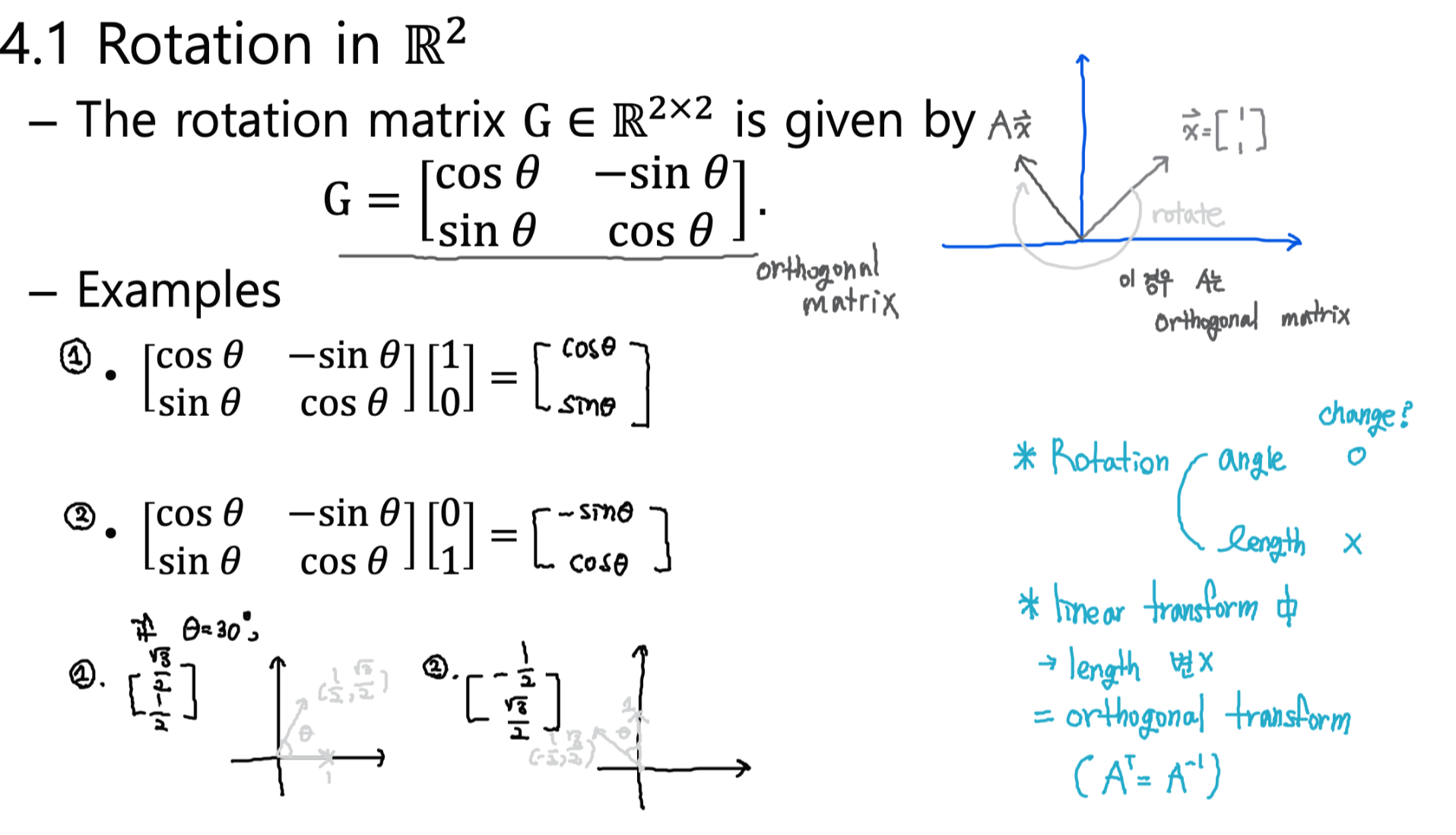
4. Rotations
- 벡터의 크기는 변하지 않고 반시계 방향으로 θ만큼 회전
- 벡터 x에 orthogonal한 정방향 matrix를 곱할 경우 rotate됨
- 단, 정방향 matrix A가 orthogonal matrix이려면 칼럼들이 모두 orthonormal해야 하므로 A는 othonormal한 matrix임
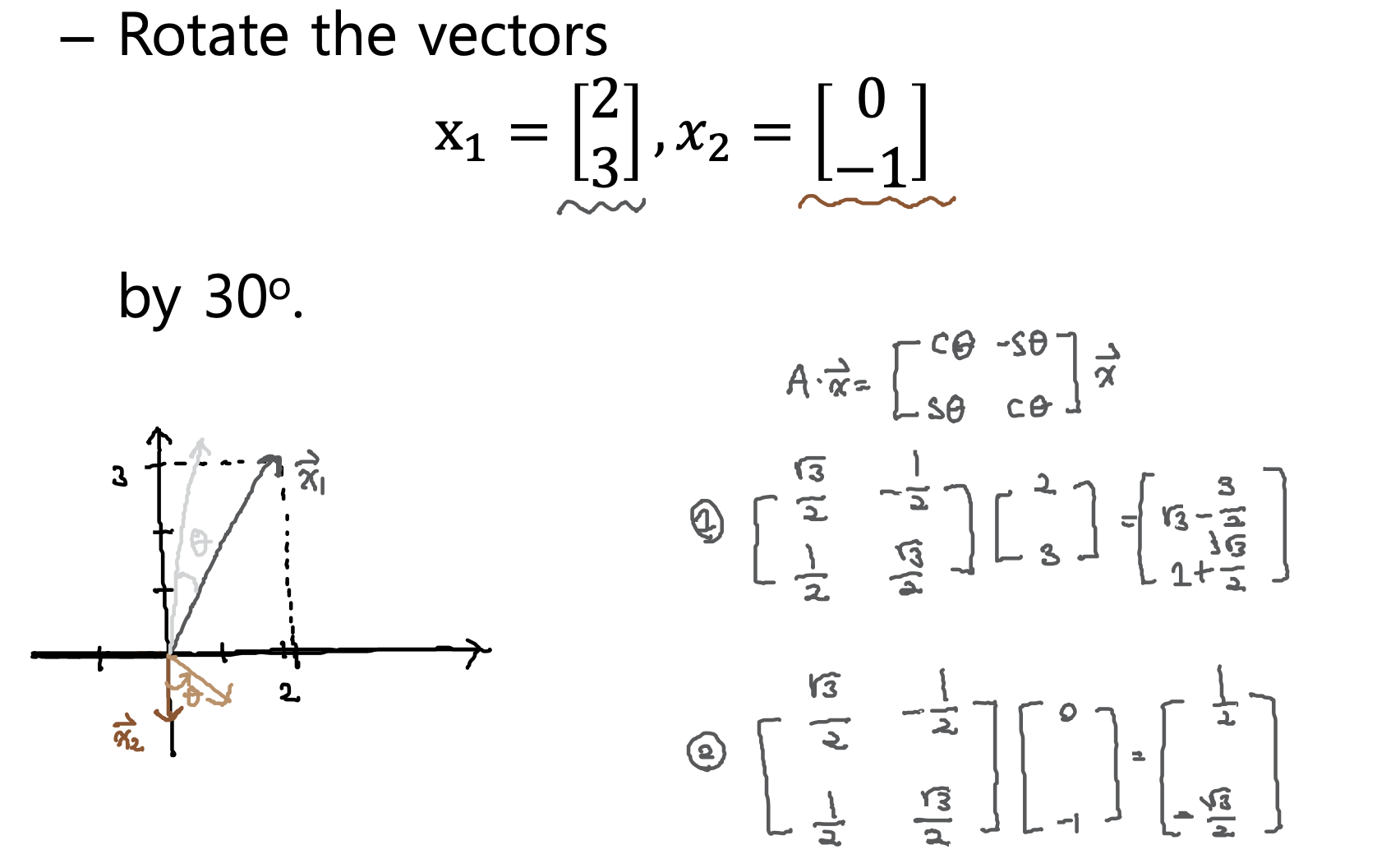
- 연습문제
+ week7 Quiz2
Q: 원본 사진을 반시계방향으로 30도 회전하려고 할 때 필요한 매트릭스는?
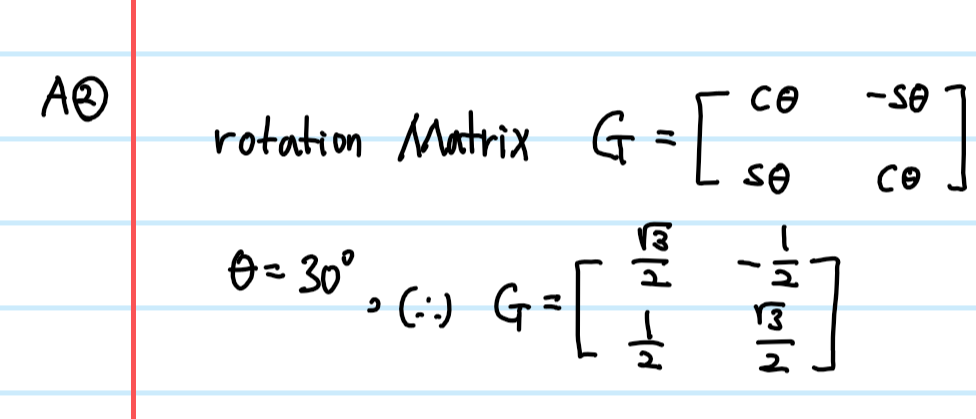

[03 Analytic Geometry] Summary
+ week6 Quiz1
두 벡터의 유사도(혹은 차이)를 측정하는데 사용하는 매트릭(matric : 방법)
1. Angle : 유사도와 비례 관계
2. Distance : 유사도와 반비례 관계
3. Inner Product : 유사도와 비례 관계