[핸즈온 머신러닝] 5. 정규화

5. Regularization

목차

5-1.  정규화

1. 과대적합

2. 비용 함수

3. 정규화된 선형 회귀

4. 정규화된 로지스틱 회귀

5. 릿지 회귀, 라쏘 회귀, 엘라스틱넷

 

5-2. 성능 측정법

 

 

 

5-1. 정규화

---

1. 과대적합

---

과대적합(overfitting)

모델이 훈련 데이터에는 너무 잘 맞지만 일반성이 떨어지는 현상

 

예시

• 만일 특성(feature)이 매우 많아지면, 훈련된 모델은 학습 데이터 셋에 매우 잘 맞을지 모름
• 그러나 새로운 데이터 샘플로 일반화되지 않을 수 있음
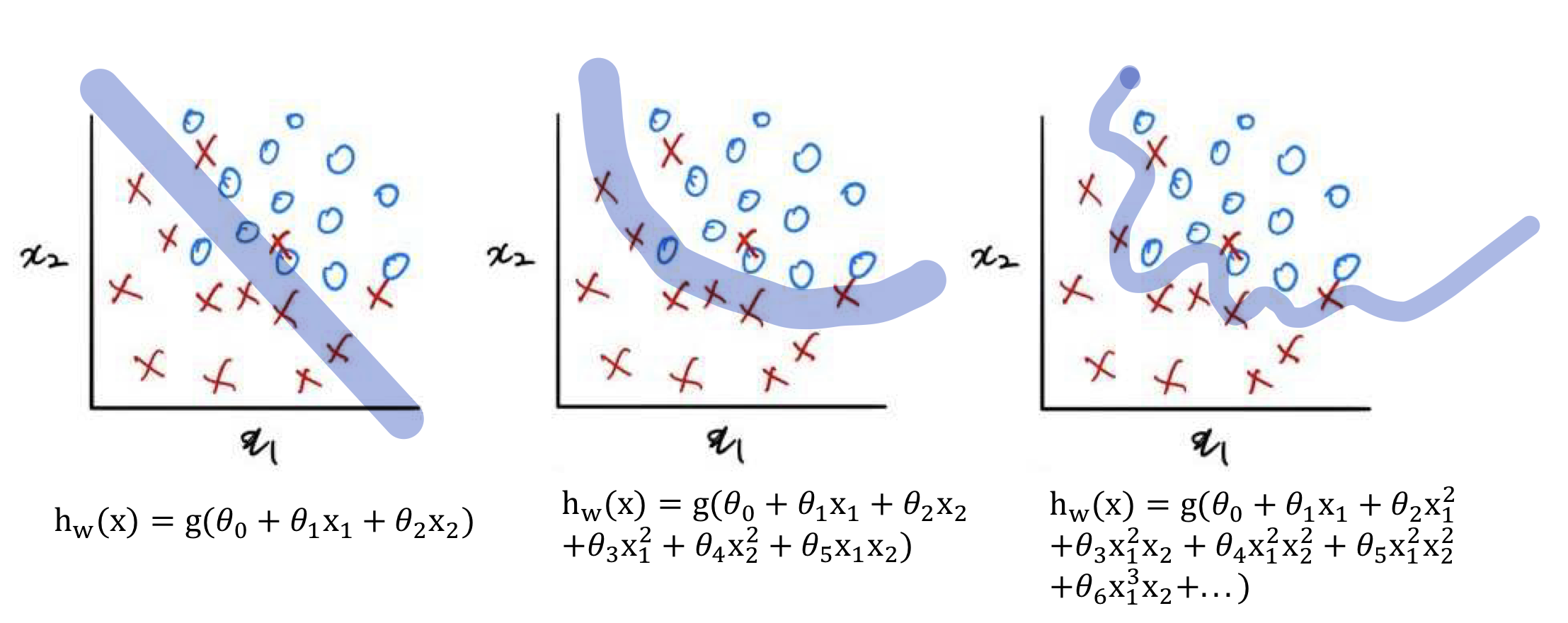
• 예로, 새로운 집 면적에 대해 집 값을 예측을 선형회귀를 이용한다고 하자.
  •  

    

  • 왼쪽부터 순서대로 과소적합(underfitting), 알맞은 모델, 과대적합(overfitting)된 모델이다
• 또한 로지스틱 회귀(분류)에서도 아래와 같이 과소적합/알맞은 모델/과대적합이 일어날 수 있다

  • 

과대적합 해결법

• 특성 개수 줄이기
  • 유지할 특성을 직접 선택
  • 모델 선택 알고리즘
• 정규화(Regularization)
  • 모든 특성은 유지한 채 파라미터 $\theta_j$의 값을 줄임
  • 특성이 많을 때 잘 작동되며, 각 특성은 y를 예측하는데 영향을 덜 끼치게 된다

 

Normalization vs. Regularization : 둘 다 정규화로 번역되나 뜻이 다름

• Normalization(Feature Scaling)
  • 값의 범위(scale)을 0~1사이로 바꾸는 것으로
  • 학습 전에 scaling함
  • 머신러닝에서 scale이 큰 feature의 영향이 커지는 것을 방지,
  • 딥러닝에서 지역 최소값에 빠질 위험 감소시킴.
• Regularization
  • weight를 조정하여 규제(제약)을 거는 기법.
  • Overfitting을 막기 위해 사용함
  • L1 규제(라쏘), L2 규제(릿지) 등의 종류가 있음

 

2. 비용함수

---

정규화의 배경

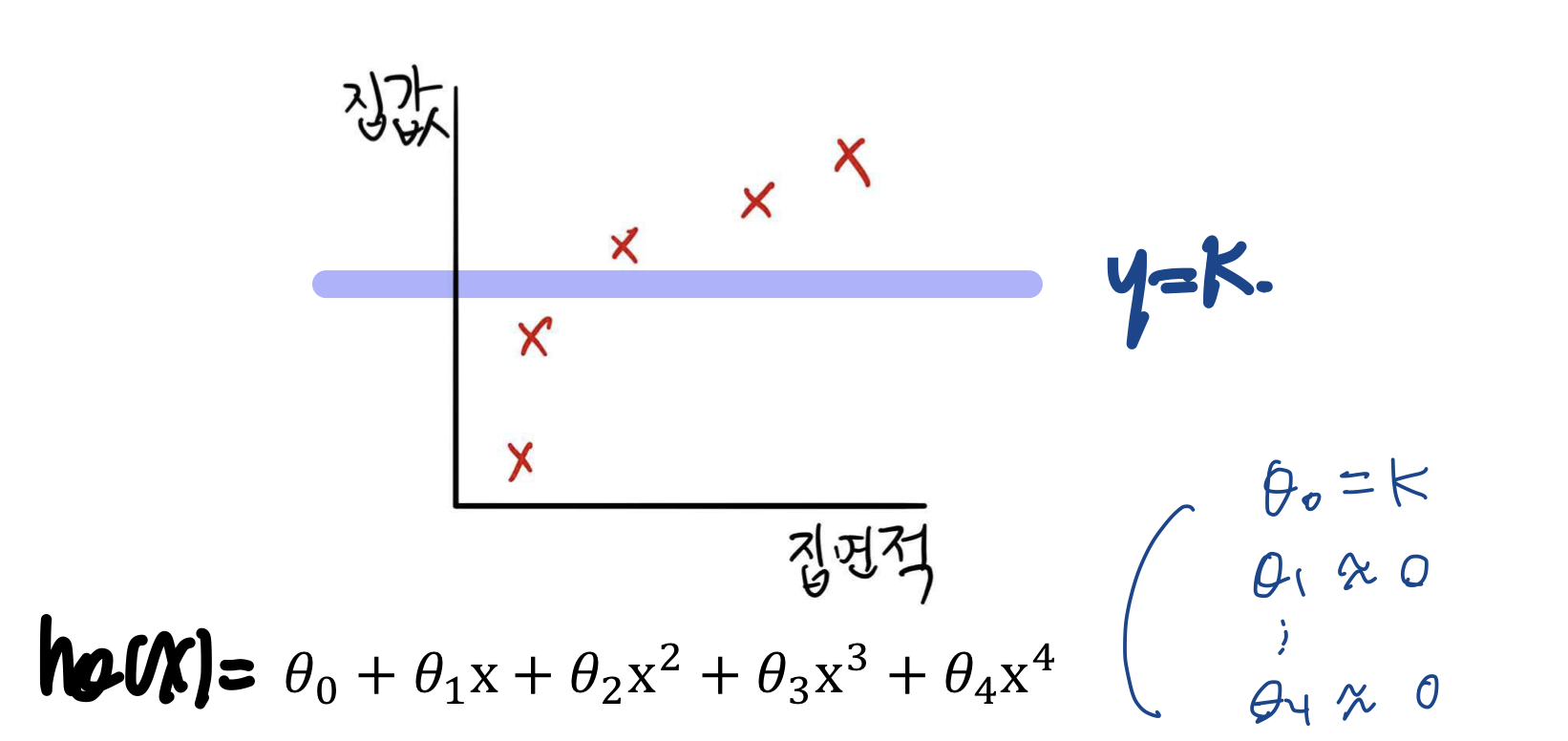
• 오른쪽의 식이 과대적합을 일으키므로, $\theta_3 x^3 + \theta_4 x^4$를 제거하자
• 즉, $\theta_3 \& \theta_4$를 매우 작게 만들자
  • 이는 기존의 비용함수에 두 항을 넣어서 실현시킬 수 있다
  • $min_\theta[\frac{1}{2m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i)^2 + 1000\theta_3^2+1000\theta_4^2]$
  • 위의 식이 최소가 되는 $\theta$를 찾도록 학습되므로, $\theta_3 \& \theta_4$를 매우 작게 만들 수 있다.
  • $\theta_3 \& \theta_4$ 앞에 각각 1000과 같이 큰 수를 곱해 비용함수에 영향을 적게 주도록 하자

 

정규화

$$J(\theta) = [\frac{1}{2m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i)^2 + \lambda \sum_{j=1}^{n} \theta_j^2]$$

• $\theta_1, \theta_2, ..., \theta_n$을 작게 하면
  • 모델 단순화
  • 과대적합 완화
  • 주의할 점은, $\theta_0$은 $\theta_0 = x_0=1$이므로 작게하는 대상에 포함되지 않는다
• 정규화 
  • 특성: $x_1, x_2, ..., x_{100}$
  • 파라미터: $\theta_1, \theta_2, ..., \theta_{100}$
• 주의사항
  • bias term($\theta_0$)은 정규화하지 않는다: 정규화  시 j=1부터
  • 비용함수에만 Regularization Term을 넣고 예측(prediction, hypothesis)시에는 RT를 넣지 않는다
  • RT는 $ \lambda \sum_{j=1}^{n} \theta_j^2$을 말함
• 목표
  • 정규화가 적용된 선형회귀에서는 위의 식을 최소화하는 $\theta$를 계산하게 됨: $min_\theta J(\theta)$

  • 

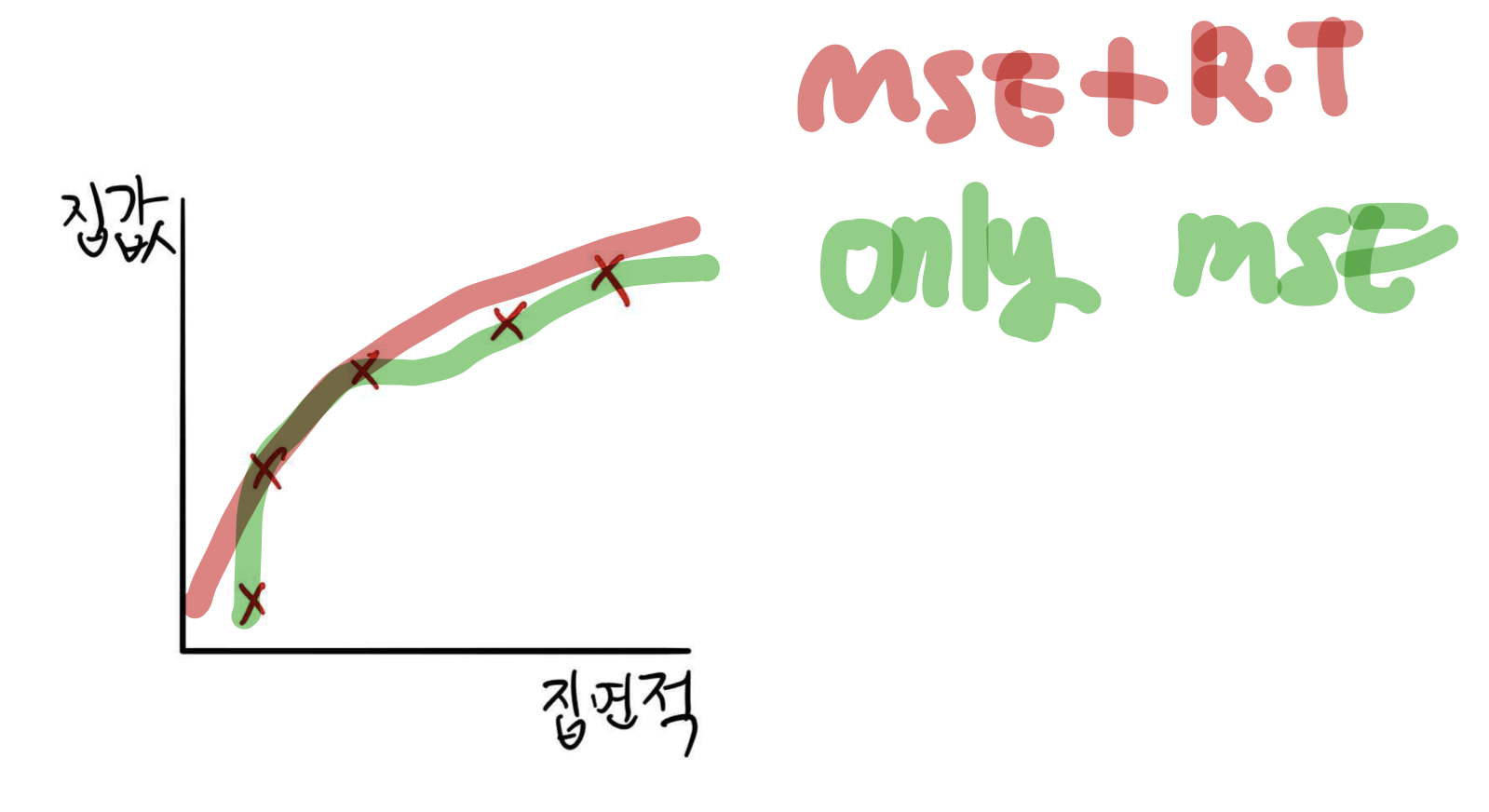
    MSE만 사용한 결과와, MES+RT를 같이 사용한 경우 비교

• 식에서 $\lambda$가 미치는 영향; $ \lambda \sum_{j=1}^{n} \theta_j^2$
  • $\lambda$가 매우 크다면(예: $\lambda=10^{10}$),
  • 뒤에 곱해지는 $\sum_{j=1}^{n} \theta_j^2$이 작아야 비용함수가 작아지는 방향으로 학습되므로 모든 $\theta$는 0에 수렴한다
  •  

    

 

 

3. 정규화된 선형 회귀

---

비용함수

• $J(\theta) = [\frac{1}{2m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i)^2 + \lambda \sum_{j=1}^{n} \theta_j^2]$
  • $ \lambda \sum_{j=1}^{n} \theta_j^2$의 편미분 과정
  • $\frac{\partial}{\partial\theta_j} \lambda \sum_{j=1}^{n} \theta_j^2 = 2\lambda \theta_j$ 
  • 앞에 $\frac{1}{2m}$과 곱해져 최종적으로 더해지는 값은 $\frac{1}{2m}*2\lambda \theta_j =$ $\frac{\lambda}{m} \theta_j$임
• $min_\theta J(\theta)$

경사 하강법

• 수렴할 때까지 아래 식 반복
• $\theta_0 = \theta_0 -  \alpha \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i) x_0 ^i$
• $\theta_j = \theta_j -  \alpha [\frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i)x_j ^i + \frac{\lambda}{m} \theta_j]$
  • $=\theta_j(1 - \alpha \frac{\lambda}{m}) -  \alpha\frac{1}{m} \sum_{i=1}^{m}(h_{\theta}(x^i)-y^i)x_j ^i$

 

4. 정규화된 로지스틱 회귀

---

가설

$$h_w(x) = g(\theta_0 + \theta_1x_1 + \theta_2x_1^2 + \theta_3x_1^2x_2 + \theta_4x_1^2x_2^2 + \theta_5 x_1^2x_2^2 + \theta_6x_1^3x_2 + ...)$$

 

 

비용함수

• $J(\theta)=-[\frac{1}{m}\sum_{i=1}^{m}y^i log(h_\theta(x^i))+(1-y^i)log(1-h_\theta(x^i))]+RT$ : cost function(cross entropy)
• $RT=\frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2$ : regularization term
•  

  

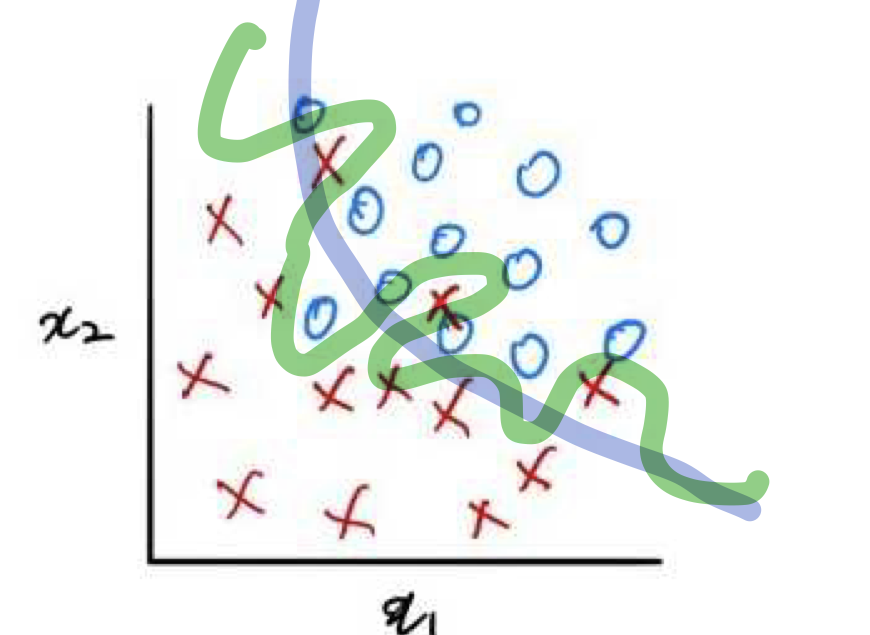
  비용함수만 사용한 경우(초록색 선), 비용함수+RT 경우(파란색 선)

 

경사하강법

• 수렴할 때 까지 아래 식 반복
• $\theta_0 = \theta_0 -  \alpha \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i) x_0 ^i$
  • $\frac{\partial}{\partial \theta_0} J(\theta)$
  • $=  \alpha \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i) x_0 ^i$
• $\theta_j = \theta_j -  \alpha [\frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i)x_j ^i + \frac{\lambda}{m} \theta_j]$
  • $\frac{\partial}{\partial\theta_j} J(\theta)$
  • $= \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i)x_j ^i + \frac{\lambda}{m} \theta_j$
  • 단, $h_\theta(x) = \frac{1}{1+e^{-\theta^T x}}$

 

5. 릿지회귀, 라쏘회귀, 엘라스틱넷

---

선형회귀버전

회귀	비용함수
릿지 회귀 (Ridge, or Tikhonov Regularization)	$J(\theta)= MSE(\theta) + \lambda \frac{1}{2} \sum_{j=1}^{n} \theta_j^2$
라쏘 회귀 (Least absolute shrinkage &selection operator)	$J(\theta)= MSE(\theta) + \lambda \sum_{j=1}^{n} |\theta_j| $
엘라스틱넷(Elastic net)	$J(\theta)$ $=MSE(\theta) + r \lambda \sum_{j=1}^{n} |\theta_j| + (1-r) \lambda \frac{1}{2} \sum_{j=1}^{n} \theta_j^2$

 

선택요령

• 보통 선형회귀 vs. 릿지 vs. 라쏘 vs. 엘라스틱 넷
• 보통 규제가 없는 선형회귀는 피함, 릿지가 일반적으로 선호됨
• 릿지 < 라쏘, 엘라스틱넷
  • 실제 영향력 있는 특성이 몇 개뿐이라고 생각 될 때
  • 불필요한 특성의 파라미터를 강하게 0로 만듦
• 라쏘 < 엘라스틱넷
  • 특성의 개수 > 훈련 데이터 개수 일 때
  • 몇몇 특성이 서로 강하게 연관되어 있을 때