[핸즈온 머신러닝] 2장. 단항 선형 회귀
2. Linear Regression with one variable
목차
1. 선형회귀란?
2. 모델설계
3. 비용 함수
4. 경사 하강법
1. 선형회귀란?

회귀(Regression)
- 연속적인 종속 변수(y)와 한 개 이상의 독립 변수(x) 사이의 관계를 추정하는 통계적인 과정
- 종속 변수 : y, 결과 변수
- 독립 변수: x, (입력) 특성
- 관계: 모델(model), 가설(hypothesis)
회귀의 종류
- 특성의 개수에 따라
- 단항 선형 회귀: 특성 개수 한 개
- 다항 선형 회귀: 특성 개수 두 개 이상
- 정규화 방법에 따라
- 릿지 회귀
- 라쏘 회귀
- 엘라스틱넷
선형 회귀(Linear Regression)
- 특성의 가중치 합과 편향(bias) 상수를 더해 결과 변수를 예측하는 과정
- 단항 $\hat{y} = h_\theta(x) = \theta_0 + \theta_1x $
- 다항
- $h_\theta(x) = \theta_0 + \theta_1x + \theta_2x_2$
- $h_\theta(x) = \theta_0 + \theta_1x + \theta_2x_1^2$
- $h_\theta(x) = \theta_0 + \theta_1x + \theta_2x_2 + \theta_3x_3 + ... $
- 활용 예
- 키와 체중의 관계 분석하기
- 몸무게, 나이, 키로 기대 수명 예측하기
- 집 면적과 집 값의 관계 분석하기
- 현재 시상 상태와 추가 정보로 미래 주식 예측하기
- 유튜브에서 특정 비디오를 보는 사용자의나이 예측하기
2. 모델설계
모델 설계(Model Representation)
-

여기서 h는 단항 선형 회귀 모델 - h 표현 방식 : $h_\theta(x) = \theta_0 + \theta_1x$, 줄여서 $h(x)$
- 여기서 $\theta$는 h를 결정하는 parameter

예시 : A 지역 근처 아파트 & 오피스텔 매매가격(57건)

- m = 훈련 예제 개수, x = 입력 변수/특성, y = 출력 변수/타겟 변수, n = 특성 개수
- 모델 h

3. 비용함수
비용함수(Cost Function)란?
- 모델이 틀린 만큼 비용(패널티)를 준다는 의미로 비용함수라고 부름
- 모델이 실제 데이터와 차이를 부정적인 의미인 손실로 간주하여 손실 함수(Loss Function)라고도 함
- 주어진 데이터에 대해, 예측된 값($\hat{y}$)과 실제 값(y) 사이의 에러를 하나의 실수값으로 수치화한 함수
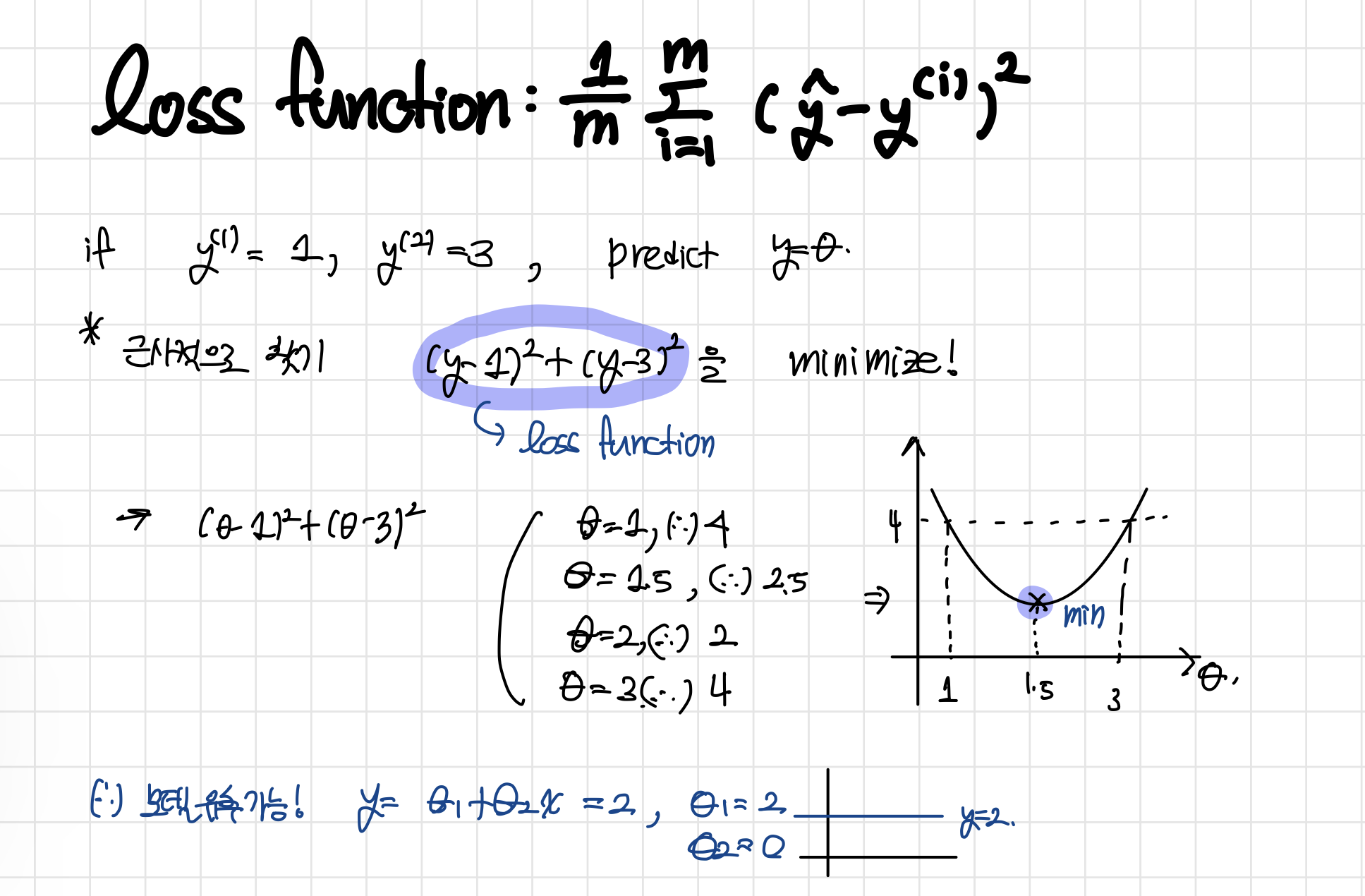
- 예) 비용함수 계산
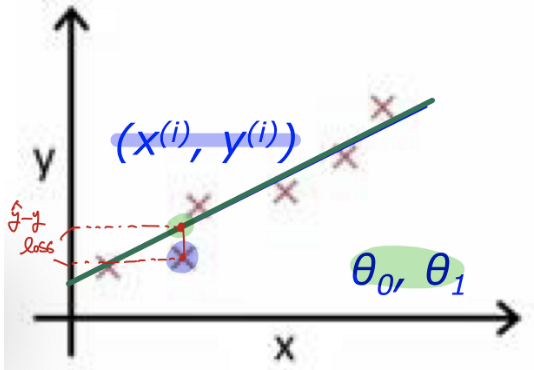
아이디어
학습 예제 (x,y)의 y와 $h_\theta(x)$가 잘 맞도록 $\theta_0, \theta_1$을 선택하자 ($h_\theta(x)$는 $\hat{y}$라고도 함)
비용함수 식
- 가설(Hypothersis) : $h_\theta(x) = \theta_0 + \theta_1x$
- 비용함수(Cost Function): $J(\theta_0, \theta_1)$
- 비용함수를 평균 제곱 오차(Mean Squared Error Function, MSE)으로 정의
-

- 목표: $argmin_{\theta_0,\theta_1}J(\theta_0,\theta_1)$
- 즉, 비용함수를 최소화하는 $\theta_0, \theta_1$를 찾는 것
단순화: $\theta_1$만 이용하는 예
-
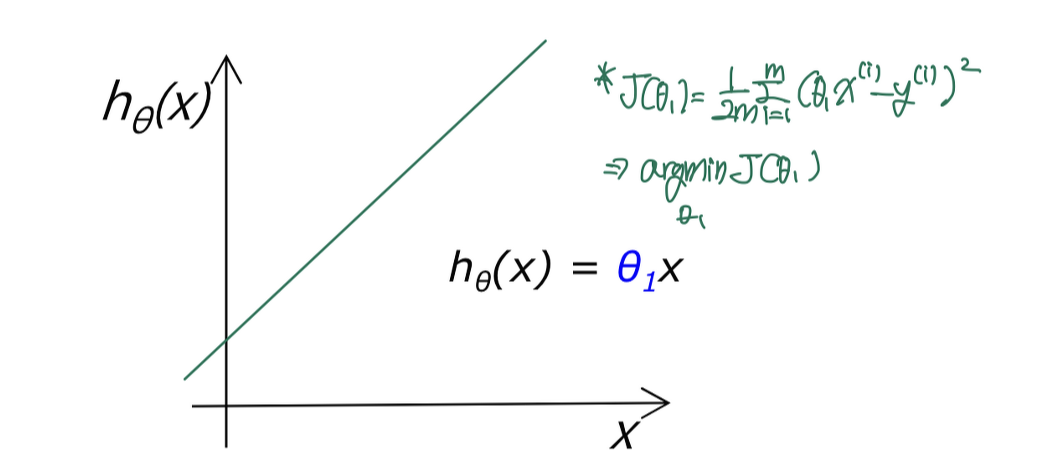
- $\theta_1 = 1$일 때 $J(\theta_1)$?
- $\theta_1 = 0.5$일 때 $J(\theta_1)$?
즉, 모델이 데이터에 덜 맞을수록(fit)할 수록 비용함수는 커지는 것을 알 수 있음

- $\theta_0, \theta_1$를 모두 이용하는 예
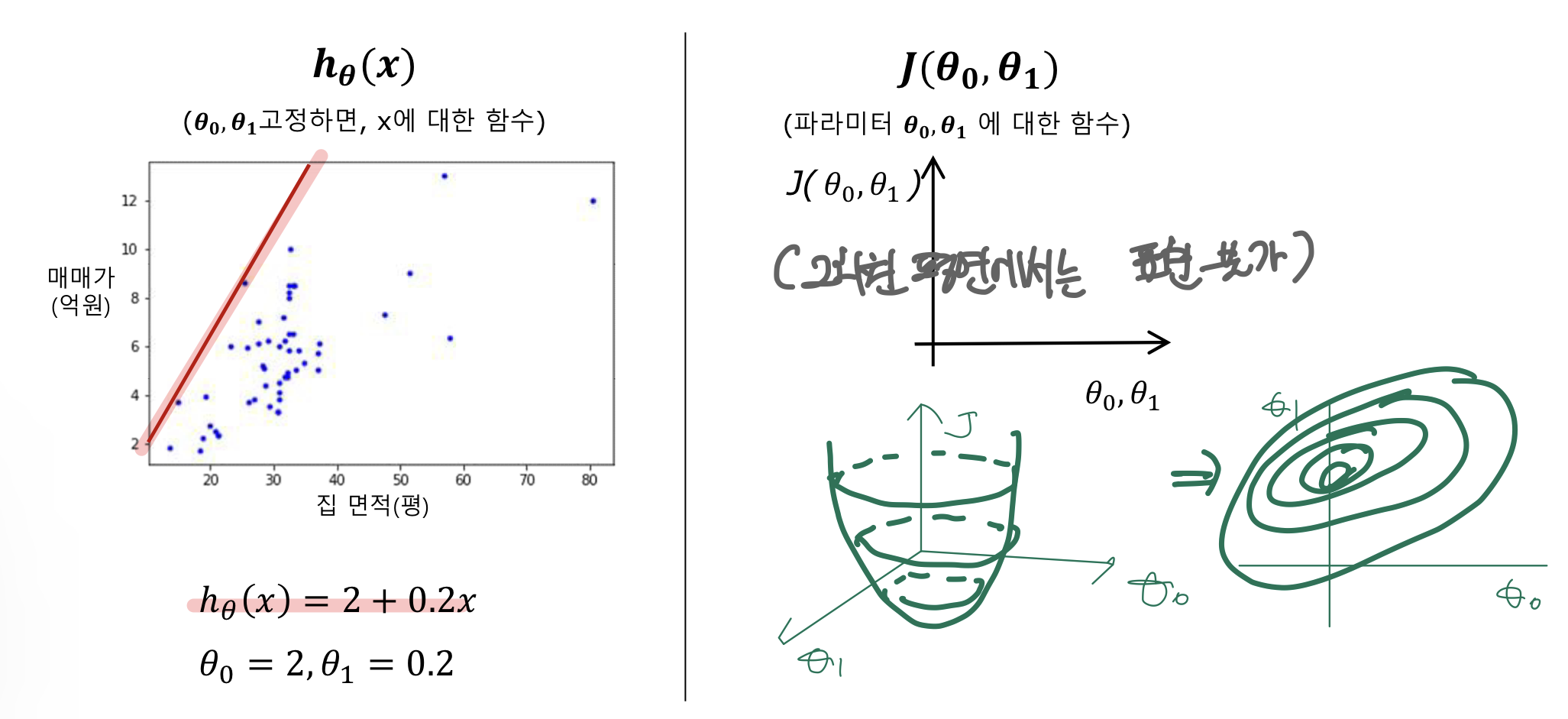
h(x) = 2 + 0.2x일 때, 비용함수 J 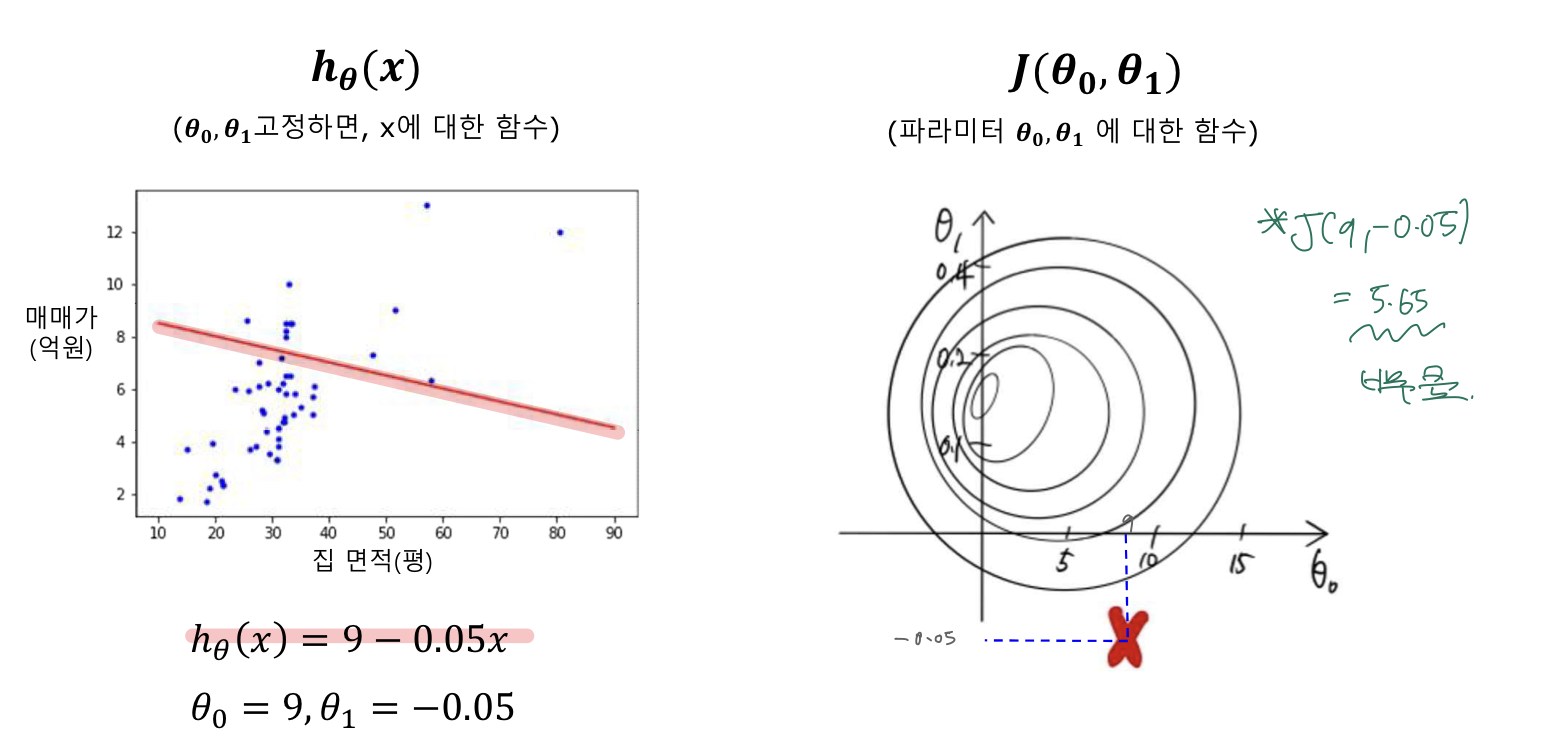
h(x) = 9 - 0.05x일 때, 비용함수 J 
h(x) = 6 + 0x일 때, 비용함수 J 
h(x) = 0.51 + 0.16x일 때, 비용함수 J
4. 경사 하강법
경사하강법(Gradient descent)이란?
- 미분 가능한 함수의 (지역)최소값을 찾기 위해 반복적으로 미분을 이용하는 최적화 알고리즘
- 함수 $J(\theta_0,\theta_1)$가 있을 때, 이를 최소화(minimize)하는 것이 목표
- 방법
- 임의의 $\theta_0,\theta_1$ 부터 시작
- $\theta_0,\theta_1$를 바꿔가며 $J(\theta_0,\theta_1)$를 희망하는 최소값에 도달할 때까지 줄임
경사하강법 알고리즘
- 아래의 식을 수렴할 때까지 반복
- $\theta_j = \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)$, (for j=0 and j=1)
- $\alpha$ : 학습률(Learning rate)
- $\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)$ : 변화율 -> 미분(derivative)
- 주의할점: 업데이트 되는 변수 $\theta_0,\theta_1$는 동시에 업데이트되어야 함
- Incorrect : 두 변수를 따로 업데이트 하는 경우
- $\theta_0 = \theta_0 - \alpha\frac{\partial}{\partial\theta_0}J(\theta_0,\theta_1)$
- $\theta_1 = \theta_1 - \alpha\frac{\partial}{\partial\theta_1}J(\theta_0,\theta_1)$
- Correct : 동시에 업데이트
- $\begin{pmatrix} \theta_0 \\ \theta_1 \end{pmatrix}=\begin{pmatrix} \theta_0 \\ \theta_1 \end{pmatrix}-\alpha\begin{pmatrix} \alpha\frac{\partial}{\partial\theta_0}J(\theta_0,\theta_1) \\ \alpha\frac{\partial}{\partial\theta_1}J(\theta_0,\theta_1) \end{pmatrix}$
- Incorrect : 두 변수를 따로 업데이트 하는 경우
j=1일때, 편미분 결과
-

- 예:) $\alpha=1$일 때
- 예:) $\alpha=0.75$일 때
경사하강법 특징
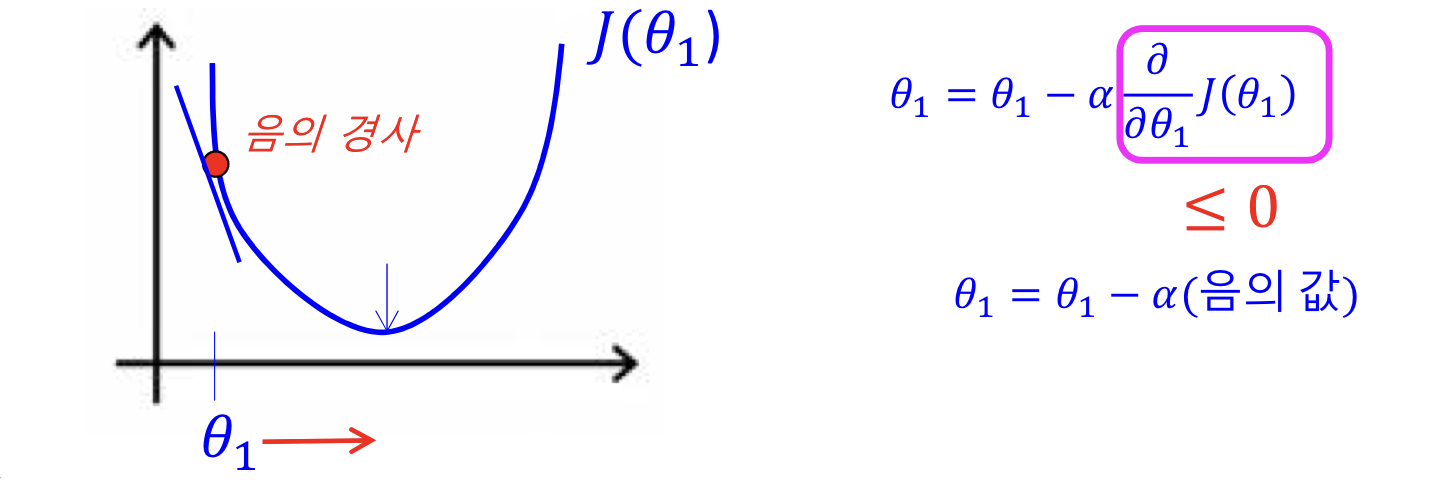
- 양의 경사인 경우, $\theta_1$ 이 음의 방향으로 이동
- 음의 경사인 경우, $\theta_1$ 이 양의 방향으로 이동
$\alpha$의 크기가 경사하강법에 미치는 영향

alpha가 너무 큰 경우(좌), alpha가 너무 작은 경우(우) - $\alpha$가 너무 큰 경우, 최소값을 지나칠 수 있음. 즉 수렴에 실패하게 되고 발산하기도 함
- $\alpha$가 너무 작은 경우, 경사하강법이 느려질 수 있음
$\alpha$를 고정하더라도, 경사 하강법은 극소에 수렴할 수 있음
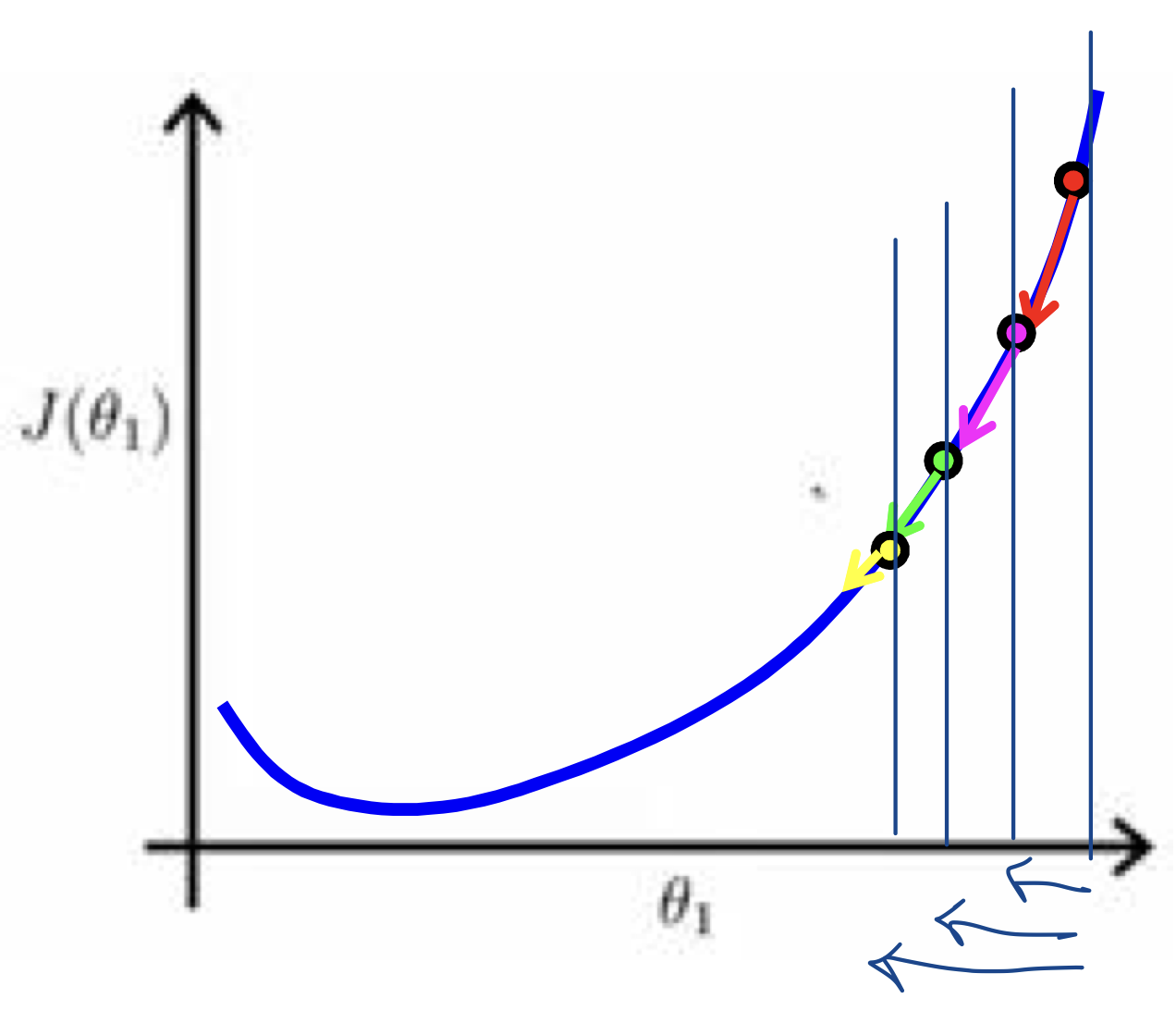
- 기울기가 작아지는 방향으로 학습하므로 $\alpha$를 조정하지 않아도 극소에 수렴 가능
- 즉, 극소에 수렴할 때 경사하강법은 자동으로 조금씩 이동하게 됨
- 따라서 반복 시, 후반부에 따로 $\alpha를 줄일 필요 없음
지역적 최소값(local minimum), 즉 극소에 위치하면 경사(기울기)가 0이되므로 더 이상 움직이지 않음
- $\theta_1 = \theta_1 - \alpha\frac{\partial}{\partial\theta_1}J(\theta_0,\theta_1)$
- 지역적 최소값에서 기울기 즉, $\frac{\partial}{\partial\theta_1}J(\theta_1)=0$임
- 따라서 $\theta_1 = \theta_1 - \alpha *0 = \theta_1$
경사 하강법 알고리즘 vs. 선형회귀 모델
- 경사 하강법 알고리즘: 수렴할 때까지 $\theta_j = \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)$, (for j=0 and j=1) 반복
- 선형회귀모델
- $h_{\theta}(x)=\theta_0+\theta_1x$
- $J(\theta)=\frac{1}{2m} \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i)^2$
선형회귀식을 적용한 경사 하강법 알고리즘

볼록 함수(Convex function)
-

- Convex 공간
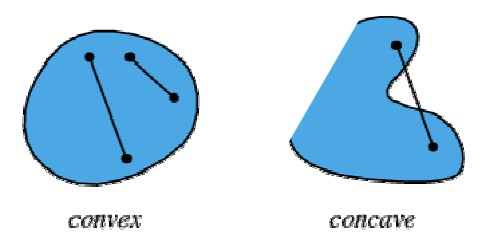
- 어떤 공간의 아무 두 점을 이은 선분이 모두 그 공간에 포함되어 있어야 함
- Convex function의 성질

- 초기점(Initial point)를 아무 점으로 설정해도 지역 최소값(local minimum)이 오직 1
- 이차 미분을 사용하여 convex function인지 아닌지 확인
- convex 함수인 경우, 지역 최소값이 한 개이므로, 경사 하강법의 비용함수로 좋음
경사하강법의 종류
- 배치 경사 하강법(batch gradient descent): 파라미터를 1회 업데이트 시킬 때 전체 학습 예제들을 사용
- 확률적 경사 하강법(stochastic gradient descent(SGD): 1회 업데이트 시, 무작위로 딱 한 개의 학습 예제 사용
- 미니배치 경사 하강법(mini-batch gradient descent): 1회 업데이트 시, 미니배치라 부르는 임의의 작은 학습 예제 샘플 사용
경사하강법에 더 자세한 내용을 알고싶다면 아래 게시글을 참고해주세요
https://codingsmu.tistory.com/86?category=987803
[DL] 경사하강법과 손실함수
선형 회귀(Linear Regression) 선형 회귀는 머신러닝 알고리즘 중 가장 간단하면서도 딥러닝의 기초가 되는 개념이다 1차 함수로 이해하는 선형 회귀 $y=ax+b$ : 선형 회귀는 1차 함수로 표현 가능하다.
codingsmu.tistory.com